Un po' di storia

Il postulato delle parallele (o V postulato di Euclide) era stato considerato già dai geometri greci come un postulato "particolare", cioè un postulato che aveva un carattere diverso rispetto agli altri postulati. Euclide stesso nel I libro degli Elementi, ritarda il più possibile l'uso di tale postulato e mette sempre in evidenza i risultati che si possono ottenere indipendentemente da esso.
In effetti in seguito si è dimostrato che il postulato delle parallele è indipendente dagli altri, cioè esistono geometrie nelle quali sussistono tutti i postulati meno quello, tali geometrie sono dette: geometrie non euclidee.
Possiamo considerare fondatori di tale geometria N.I. Lobacewski, matematico russo (1793-1856), e G. Bolyai, matematico ungherese (1802-1860).
Per Lobacewski la geometria è quella dei corpi solidi e partendo da essi, tramite un processo di astrazione, si possono determinare gli enti primitivi: punto, retta, piano. Questi enti hanno quindi un significato fisico, i postulati che ne caratterizzano le relazioni hanno un carattere sperimentale, concreto. In seguito al fine di dimostrare la consistenza di queste nuove geomentrie vennero creati dei modelli ad opera di Beltrammi, Klein e Poincaré. La sistemazione di questi concetti avviene sessant'anni dopo il libro di Lobacewski, Nuovi principi, ad opera di David Hilbert, in Grundlagen der Geometrie.

Gli assiomi di Hilbert

Gli assiomi di Hilbert postulano l'esistenza di concetti primitivi quali punto, retta, appartenere a, giacere tra. Essi sono definiti implicitamente dalle relazioni formali espresse in quattro gruppi di assiomi.

Assiomi di Hilbert
Assiomi di incidenza
  • Due punti distinti, presi a piacere, appartengono ad una retta e ad una soltanto.
  • Ad ogni retta appartengono perlomeno due punti.
  • Esistono due punti, non appartenenti ad uan medesima retta.
Assiomi d'ordine
  • Se B giace tra A e C,(e scriviamo A*B*C), allora A, B, C sono tre punti distinti di una retta. Vale inoltre C*B*A.
  • Dati due punti A e B a piacere, si può sempre trovare un terzo punto C tale che A*B*C.
  • Dati tre punti su una retta, ne esiste uno ed uno soltanto che giace tra i rimanenti due.
  • Assioma di Pasch. Siano A, B, C tre punti non allineati e sia l una retta che non contiene nessuno di questi punti. Se l contiene un punto D che giace tra A e B, allora l deve contenere anche un punto che giacia o tra A e C o tra B e C.
Assiomi di congruenza fra segmenti

  • Dato un segmento AB e dato un raggio r con origine in C, esiste un unico punto D del raggio r tale che AB è congruente a CD, AB=CD.
  • Se AB=CD e AB=EF, allora CD=EF. Ogni segmento è congruente a se stesso.
  • Addizione. Dati tre punti A, B, C su una retta tali che A*B*C, e dati altri tre punti D, E, F su un'altra retta tali che D*E*F; se AB=DE e BC=EF, allora AC=DF.
Assiomi di congruenza fra angoli

  • Dato un angolo BAC e un raggio DF, esiste un unico raggio DE, da un lato fissato della retta DF, tale che BAC è congruente a EDF, BAC=EDF.
  • Per ogni tre angoli a, b, c, se a=b e a=c, allora b=c. Ogni angolo è congruente a se stesso.
  • Dati due triangoli ABC e DEF, supponiamo che AB=DE, AC=DF e gli angoli BAC=EDF. Allora i due triangoli sono congruenti, cioè BC=EF, ABC=DEF e ACB=DFE.

Si definisce piano di Hilbert l'insieme costituito da punti, da sottoinsiemi detti rette e da nozioni primitive d'ordine e di congruenza che soddisfa gli assiomi di Hilbert.
Si definisce geometria non euclidea un piano di Hilbert in cui non vale il postulato delle parallele.

Geometria non euclidea

Analizziamo le geometrie non euclidee partendo dai risultati ottenuti da Saccheri, (1667-1733). L'opera di Saccheri sfortunatamente non ebbe subito i riconoscimenti che meritava e venne rivalutata solo nel diciannovesimo secolo.

In un piano di Hilbert, supponiamo di avere due segmenti congruenti AC, BD perpendicolari e posti agli estremi di un intervallo AB. Congiungiamo C e D, questa figura è detta quadrilatero di Saccheri. Gli angoli in C e D sono congruenti.

TEOREMA DI SACCHERI

In qualsiasi piano di Hilbert, se un quadrilatero di Saccheri ha gli angoli in C e D acuti (o retti o ottusi), allora tutti i quadrilateri di quel piano hanno gli angoli acuti (o rispettivamente retti o ottusi).

Questo risultato ci permette di dimostrare un'importante proprietà dei piani non euclidei: la somma degli angoli interni di un triangolo non è pi-greco. Infatti vale la seguente proposizione: dato un triangolo ABC, esiste un quadrilatero di Saccheri per cui la somma dei due angoli in alto è pari alla somma dei tre angoli del triangolo.

TEOREMA

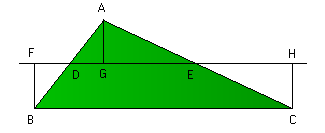
In qualsiasi piano di Hilbert, se esiste un triangolo la cui somma degli angoli è minore (o maggiore o uguale) a pi-greco, allora ogni triangolo ha la somma degli angoli minore (o rispettivamente maggiore o uguale) a pi-greco.

Diremo che un triangolo è euclideo se la somma dei suoi angoli è pi-greco, altrimenti lo chiameremo non euclideo. Per misurare la diversità dal caso euclideo, definiamo difetto di ogni triangolo di essere pi-greco.

Il modello di Poincaré

Dimostreremo l'esistenza della geometria non euclidea esibendo un modello che sarà costruito con le componenti logiche della geometria euclidea. Daremo cioè un'interpretazione delle nozioni indefinite di punto, retta, ordine e verificheremo la validità degli assiomi di Hilbert.

Il nostro punto di partenza è un piano cartesiano su un campo euclideo e ordinato F. In questo piano consideriamo un cerchio fisso C di centro O.
I punti del nostro modello (che chiameremo P-punti) saranno i punti del piano che giacciono all'interno di C, non terremo in considerazione i punti che giacciono sulla circonferenza C. Una P-retta sarà l'insieme di tutti i P-punti che giacciono su una circonferenza ortogonale a C o quelli che giacciono su una retta passante per O. Precisiamo che quando parliamo di punti, rette, cerchi, ci riferiamo alle nozioni euclidee, quando invece aggiungiamo a queste parole il prefisso P allora ci stiamo riferendo al concetto corrispondente del modello che stiamo costruendo.

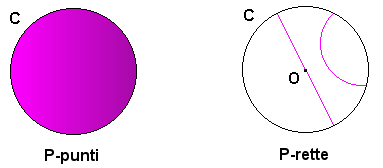
Una volte definiti anche i concetti di ordine e congruenza si dimostra che il modello di Poincaré soddisfa gli Assiomi di Hilbert, non verifica invece quello delle parallele.

PROPOSIZIONE

L'assioma delle parallele non vale all'interno del modello di Poicaré: dati una P-retta, r, e un P-punto, A, esistono più P-rette passanti per quel punto che non incontrano la P-retta r.

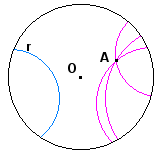
Ricordiamo che due rette si dicono parallele quando non si incontrano!

Geometria Iperbolica

ASSIOMA DI IPERBOLICITA'

Per ogni retta l e ogni punto A non appartenente ad l, esistono due raggi Aa e Aa' uscenti da A, che non giacciono sulla stessa retta, che non incontrano l, cioè ogni raggio interno all'angolo aAa' incontra l.

Questo assioma implica necessariamente che tale geometria è non-euclidea perchè i due raggi Aa e Aa' giacciono su due rette distinte passanti per A che sono entrambe parallele a l.
Definiamo piano iperbolico un piano di Hilbert che soddisfa l'assioma di iperbolicità.
Si può dimostrare che in un piano iperbolico, la somma degli angoli interni di un triangolo è minore di un angolo piatto.

Nella produzione di Escher gli anni che vanno dal 1956 al 1970 individuano quello che possiamo definire: Periodo dell'Infinito. L'opera migliore di questo periodo è Limite del cerchio III (1959), che sembra sia il frutto dell'ammirazione dell'artista per una illustrazione di un libro di H.S.M. Coxeter. Quest'immagine è un arappresentazione di uno spazio iperbolico il cui modello è dovuto al matematico francese Poincarè. Diamo un'idea dello spazio che Escher ha voluto rappresentare. Poniamoci al centro del disegno e supponiamo di voler camminare fino al bordo di esso. Mentre camminiamo ci restringiamo sempre di più, proprio come accade ai pesci della figura. Per raggiungere il bordo quindi dovremmo percorrere una distanza che ci sembrerà infinita, ma essendo immersi in questo spazio non ci parrà subito ovvio che ci sia qualcosa di inusuale.
Questa rappresentazione dell'infinito anticipa di qualche decennio la formulazione matematica del concetto di frattale ad opera di Beniot B. Mandelbrot.
Anche l'ultima opera della sua vita, Serpenti (1969), è uno studio sull'infinito. In questo caso lo spazio si scontra con l'infinito non solo nella direzione del bordo ma anche verso il centro del cerchio, producendo un restrigimento in entrambi i sensi. Ma la stampa più igegnosa può essere considerata: Esposizione di Stampe (1956). Giudicando quest'opera secondo i canoni tradizionali dell'estetica, si potrebbero trovare una quantità enorme di difetti. Ma quello che è valido in tutta l'opera di Escher qui è esaltato all'ennesima potenza. Egli ha raggiunto in quest'opera il limite della sua perspicacia e della possibilità di espressione. In quest'immagine una persona si trova all'interno di una galleria d'arte e sta osservando una stampa raffigurante una città marittima che, lungo i portici, ospita un negozio. Quel negozio è una galleria d'arte al cui interno si trova una persona che sta osservando una stampa raffigurante una città marittima... Escher è tornato in qualche modo sul suo soggetto; la persona è sia nell'immagine che al di fuori di essa. Questo effetto è stato ottenuto grazie ad una griglia che l'artista creò in preparazione a quest'opera.
Clicca qui per vedere la griglia.