Girard Desargues
L'incompreso genio moderno

Prima della ricerca dello storico francese René Taton si credeva erroneamente che Desargues fosse nato nel 1593 perché, nella biografia di Cartesio di Adrien Baillet del 1691, si afferma che Desargues aveva tre anni più di Cartesio. Taton ha scoperto un oroscopo di Desargues che segna la sua nascita alle 6:30 del 21 febbraio 1591. Non ci sono informazioni sulla sua educazione e sulla sua vita prima dei trent'anni. Come matematico fu molto originale e completamente rigoroso. Baillet, biografo francese, affermò che Desargues fu un ingegnere coinvolto nell'assedio di La Rochelle nel 1628 e lì incontrò per la prima volta Descartes. Non c'è nessuna prova aggiuntiva a sostegno di questa affermazione, anche se, date le competenze di Desargues, appare certamente plausibile. Quando era a Parigi, Desargues prese parte al circolo matematico che si riuniva presso il padre Marin Mersenne (1588-1648). Questo includeva René Descartes (1597-1650), étienne Pascal (1588-1651) e suo figlio Blaise Pascal (1623-1662). Fu essenzialmente per questo limitato gruppo di amici che Desargues preparò le sue opere matematiche e le fece stampare. Scrisse riguardo argomenti pratici come la prospettiva in Exemple de l'une des manières universelles du S.G.D.L. touchant la pratique de la perspective sans emploier aucun tiers point, de distance ny d'autre nature, qui soit hors du champ de l'ouvrage (1636), il taglio delle pietre per l'uso nella costruzione e gli orologi solari. Ci si chiede immediatamente chi o cosa sia "S.G.D.L.", ma si tratta semplicemente dell'autore stesso, dalle iniziali di "Sieur Girard Desargues Lyonnais". Questo lavoro sulla prospettiva deve aver portato Desargues a sviluppare un nuovo approccio alla geometria. Nel 1640 Blaise Pascal, che all'epoca aveva sedici anni, produsse il suo "esagramma mistico". In esso si riferiva a Desargues:
Pascal deve riferirsi qui all'opera più importante di Desargues, quella in cui inventò la sua nuova forma di geometria, la quale ha per titolo Brouillon project d'une atteinte aux evénémens des rencontres du Cone avec un Plan. Il lavoro di Desargues sulla prospettiva portò ad una discussione molto spiacevole. Nel 1642 un'opera anonima intitolata La Perspective practique nécessaire à tous peintres, graveurs, sculpteurs, architectes, orfèvres, bordeurs, tapissiers & autres se servans du Dessein fu scritta da Jean Du Breuil (1602-1670). La prefazione del libro dette credito a Desargues, ma lui fu molto turbato nel vedere le sue idee presentate con molti errori e la sua reazione fu di mettere cartelli in tutta Parigi. Uno lo intitolò "Incredibile errore" e un altro "Enormi difetti e duplicazioni". Du Breuil contrattaccò con un pamphlet sostenendo che lo scritto di Desargues del 1636 sulla prospettiva presentasse idee già precedentemente pubblicate. Desargues continuò la discussione dettagliando gli errori nel lavoro di Du Breuil. In una lettera scritta da Jean Beaugrand, segretario del Re e scienziato, venne criticato lo studio proiettivo delle coniche di Desargues. A questo punto Desargues sembrò essersi rivolto ad Abraham Bosse per pubblicare chiarimenti sul suo lavoro e per difendersi da questi attacchi. Un nuovo attacco arrivò nel 1644 da parte di Jacques Curabelle il quale sostenne che la mancanza di esperienza pratica di Desargues rendesse il suo lavoro inutile. Egli scrisse:Dimostreremo anche questa proprietà di cui l'inventore originale è M. Desargues di Lione che è una delle grandi menti di questo tempo e uno dei più versati nella matematica, in particolare tra gli altri nelle coniche, i cui scritti su questo argomento, sebbene in numero ridotto, hanno dato ampia testimonianza della sua abilità a coloro che hanno voluto prenderne conoscenza: e ammetterò che devo il poco che ho trovato su questo argomento ai suoi scritti, e che ho cercato di imitare quanto mi è possibile il suo metodo su questo argomento.
Seguì una feroce discussione tra Curabelle e Desargues con vari opuscoli nei quali si attaccarono a vicenda ed istituirono un dibattito con regole, regolamenti e giudici nominati per decidere il vincitore che avrebbe ricevuto una grande somma dal perdente. Non ci sono prove, tuttavia, che questo abbia mai avuto luogo. Desargues sembra essersi stancato delle continue battaglie in cui era implicato e, dal 1645, si dedicò all'architettura. Nel 1648 tornò a Lione dove sembra essere stato più coinvolto nella progettazione architettonica e pubblicò poco. Si ritirò nella sua casa di campagna a Condrieu dove amava curare personalmente il proprio giardino e qui morì nel 1661. C'è da chiedersi quale altro brillante lavoro avrebbe potuto realizzare questo eccezionale matematico se non fosse stato sottoposto a critiche così diffuse.Se il detto Sieur avesse capito e praticato le cose di cui voleva parlare, probabilmente non sarebbe caduto in tali errori, essendo la pratica necessaria per aiutare a rafforzare i nostri sensi; essa confermerà o smentirà ciò che la speculazione delle nostre menti avrebbe prodotto.
Nello stesso anno in cui Claude Mydorge completava la sua opera, Prodromi catoptricorum et dioptricorum sive Conicorum operis ad abdita radii reflexi et refracti mysteria praevij et facem praeferentis, Girard Desargues pubblicava il suo breve trattato sulle sezioni coniche dal titolo: Brouillon project d'une atteinte aux evénémens des rencontres du Cone avec un Plan, traducibile come Bozza di un saggio su quello che si ottiene sezionando un cono con un piano. Nel 1679, quarant'anni dopo la prima pubblicazione del trattato, non esistevano più copie di esso. Si può dedurre da una dichiarazione di Philippe de la Hire, figlio del pittore allievo di Desargues, il quale lesse in quell'anno per la prima volta il trattato, trascrivendolo per averne una totale conoscenza. Tale copia fu ignorata per centosessantaquattro anni, e probabilmente sarebbe andata perduta, se lo storico e matematico Michel Chasles non l'avesse scovata in uno scartafaccio da un antiquario di Parigi nel 1845. Il trattato tuttora occupa centoventotto pagine del primo volume delle opere ristampate da Poudra nel 1864 (pag. 103-230).


Qua ogni linea retta è pensata allungata al bisogno all'infinito da una parte e dall'altra.
Questo oggetto, con l'invito ad andare con il pensiero all'infinito, si presenta diverso dalla retta quale segmento euclideo. La differenza diventa ancora più chiara subito dopo, quando Desargues introduce i fasci di rette (ordonnance des lignes droictes), e chiama but la "meta", il "punto" che le rette del fascio hanno in comune, una caratteristica che le lega insieme in un unico destino, una sorta di comune inclinazione verso un "dove" che può essere a distanza finita o infinita.
Vengono ora presentate le nuove definizioni introdotte all'inizio del Brouillon, nel tentativo di
creare nuove immagini mentali capaci di sviluppare un'intuizione dinamica.
L'immagine del tronco perde la propria generalità e diventa il caso particolare di albero quando
nel tronco si individua una origine: "il ceppo" e una particolare configurazione di rami e di nodi.
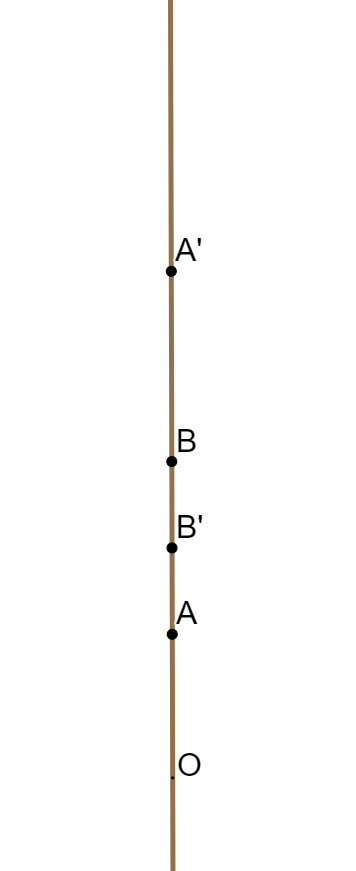
Un arbre (albero) è un tronco con une souche (un ceppo) \( O \) e varie branches couplées (getti
accoppiati o coniugati) tra loro che nascono dal ceppo e si sovrappongono al tronco. Se \(OA\) e \(OA'\) sono due tali getti accoppiati,
si richiede che il prodotto \( (OA) \cdot (OA') \) , con il giusto
segno, abbia un valore costante non nullo. La struttura ad albero permette di stabilire una
corrispondenza biunivoca (ed involutoria) tra i nodi del suo tronco, nel senso che al nodo \( A \) resta
associato in modo unico un nodo \( A' \), a \(B\) un nodo \( B'\) e così via e viceversa.
Gli accoppiamenti sono fatti in modo tale che l'area del rettangolo
che ha per lati due ramificazioni accoppiate non cambi: $$ (OA) \cdot (OA') = (OB) \cdot (OB') = costante $$
Un albero sarà dunque definito da un tronco, un ceppo e una costante (positiva o negativa) con
la quale accoppiare i getti. Il primo risultato importante di Desargues è quello di rendere la
struttura involutoria di tali nodi indipendenti dal ceppo, dandone una caratterizzazione
intrinseca. Relazione quest'ultima che non coinvolge il ceppo \(O\).
La speciale configurazione data da tre coppie di punti disposte su un tronco in modo da appartenere ad uno stesso albero come coppie coniugate,
viene chiamata da Desargues "involuzione" e la relazione
$$ \frac{(AB)\cdot (B'A)}{(A'B) \cdot (B'A')}= \frac{(AC) \cdot (C'A)}{(A' C) \cdot (C'A')} $$
ne fornisce una caratterizzazione quantitativa. è un concetto invariante per trasformazioni proiettive, strumento centrale nel metodo di Desargues.
Le involuzioni, in questo modo, si legano ad elementi grafici, formati cioè da configurazioni di rette e punti, che, come tali, sono invarianti per proiezioni centrali.
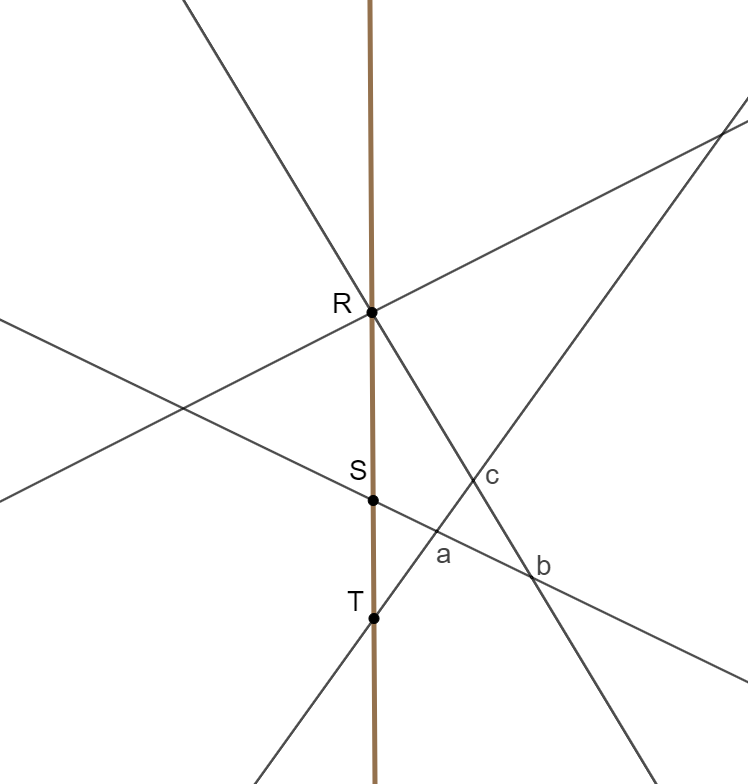
L'involuzione può essere definita, oltre che dalle due coppie di punti \(AA' \) e \(BB'\) , anche da una
coppia di punti e una coppia di rette indicate in blu nell'immagine seguente. In questo caso la
costruzione viene fatta a partire dai punti \(B\) e \(B'\) nei quali le rette date incontrano il tronco. La
coppia di rette è pensata come una "curva di ordine due", cioè come una configurazione che
interseca una qualunque retta in due punti ed è solo questa la proprietà che viene usata per
costruire l'involuzione.
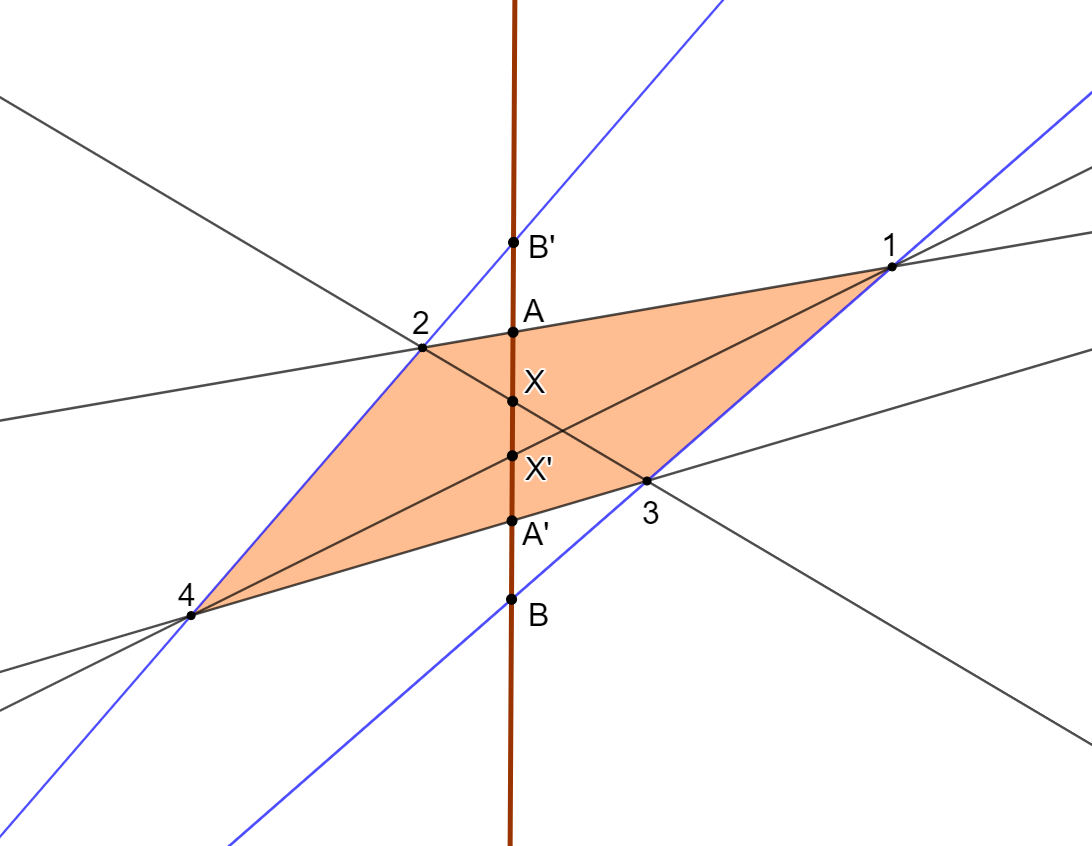
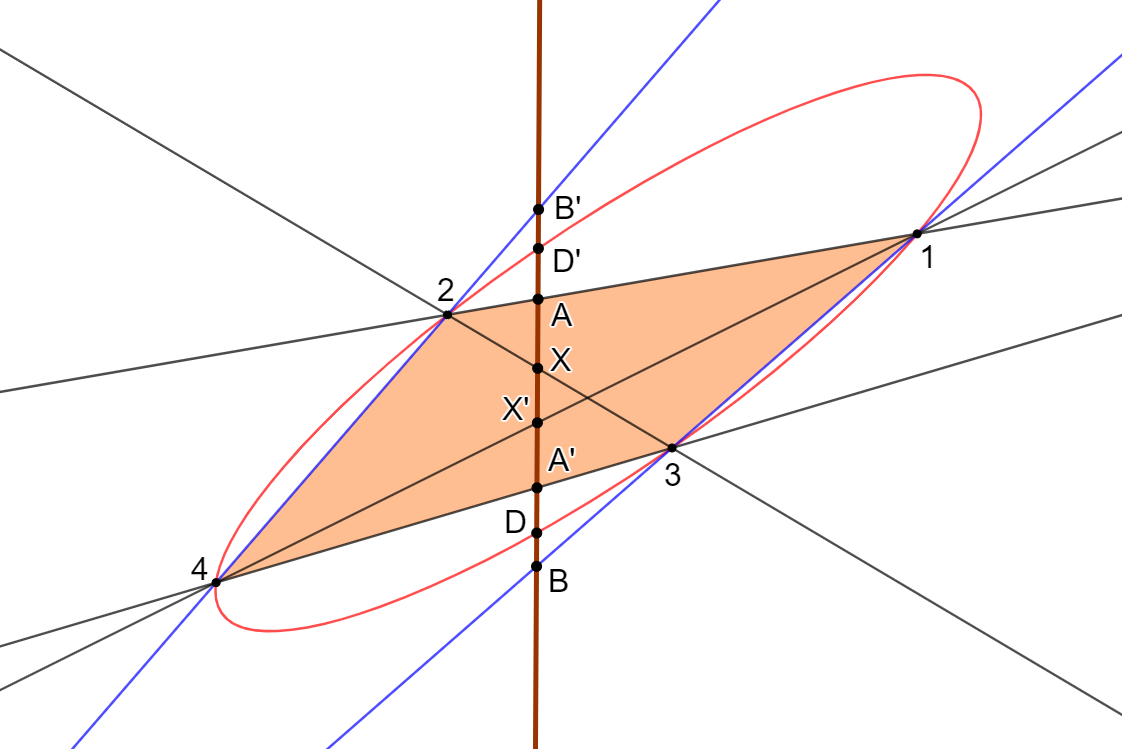
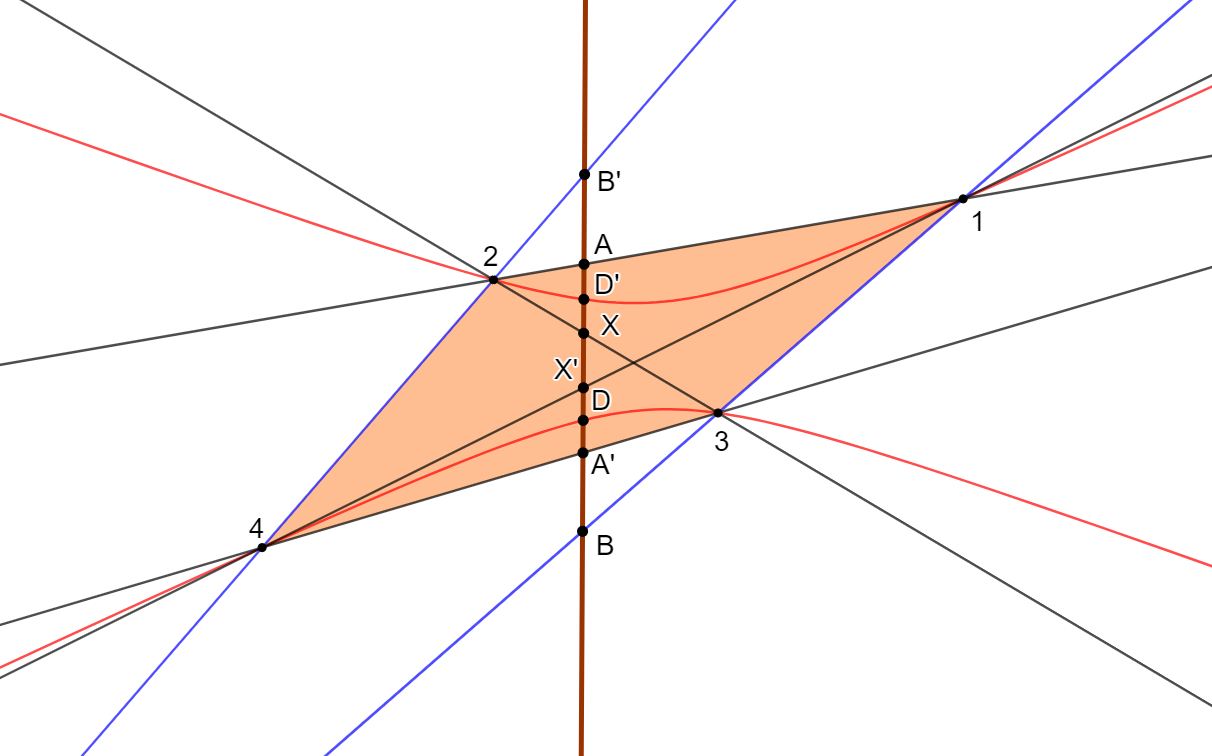
Clicca qui per la costruzione del quadrangolo con GeoGebra Clicca qui per la costruzione dell'ellisse con GeoGebra Clicca qui per la costruzione dell'iperbole con GeoGebra
Desargues riesce di fatto a dimostrare che una qualunque conica, che passi per i quattro punti 1,2,3,4, interseca il tronco in una ulteriore coppia \( DD' \), che insieme ad \( AA', BB', XX' \), appartiene alla stessa involuzione, legando in questo modo, con una geniale intuizione, le involuzioni alle coniche. Questo risultato è quello che Pascal chiamerà poi proprieté merveilleuse.
Dimostrazione nel caso in cui la conica sia una circonferenzaL'intelletto è incapace di comprendere come gli avvenimenti che il ragionamento gli fa conchiudere possono essere.
Quando il bordo di una sezione di un rotolo è una curva che a distanza finita raddoppia e si unisce a se stessa, la figura è chiamata un cerchio, o un ovale, altrimenti una ellisse (defaillement). Quando il bordo di una sezione di un rotolo è una curva che a distanza infinita raddoppia e si congiunge con se stessa, la figura è chiamata una parabola (egalation). Quando il bordo di una sezione di un rotolo è una curva che a distanza infinita si divide in due metà, rivolte all'indietro, la figura è chiamata una iperbole (excedement).Enunciato:
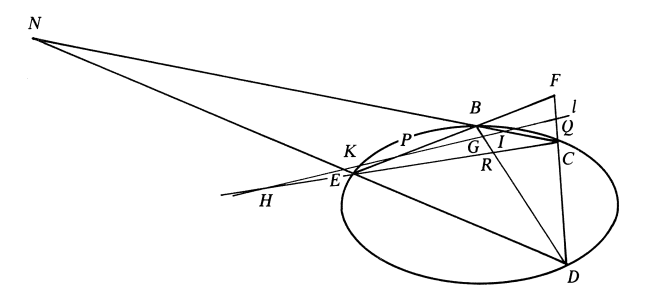
Siano \( B, C, D, E\) i quattro vertici di un quadrangolo le cui coppie di lati opposti \(BC \) e \( ED \) si incontrano in \( N \) , \( BE \) e \( CD \) in \(F \), \( BD \) e \(CE\) in \(R\). Allora le coppie di linee incontrano qualsiasi altra linea, \(l\) , in sei punti che sono in involuzione. Inoltre, qualsiasi conica passante per \( B, C, D, E \) e qualsiasi coppia di lati del quadrangolo, incontra anche la retta \( l \) in sei punti in involuzione.