Dimostrazione nel caso della circonferenza

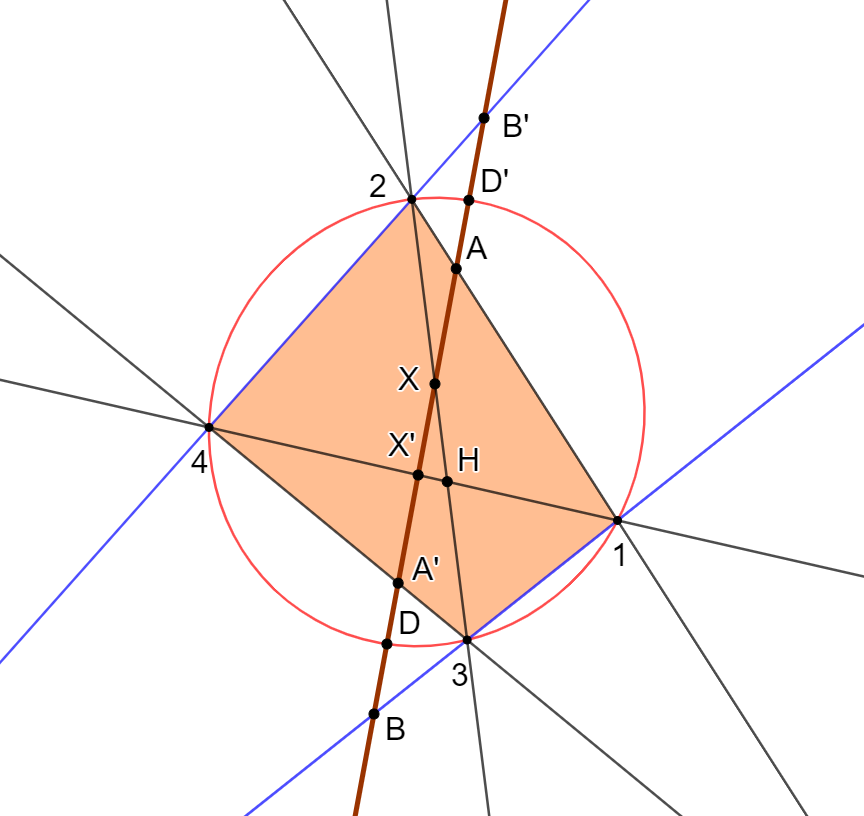
Costruzione della circonferenza con GeoGebra

Nel caso che la conica sia una circonferenza, si applica il Teorema di Menelao al triangolo \( AHA'\) tagliato dalla trasversale \(X' 1\) e dalla trasversale \( X2 \) e si utilizza il fatto che \( 3H \cdot 2H = 4H \cdot 1H \) (Euclide, Elementi, Libro III, proposizione 35). Con questo si vede che il rapporto tra i rettangoli \( \frac{AX' \cdot AX}{A'X' \cdot A'X} \) coincide con il rapporto \( \frac{A1 \cdot A2}{A'3 \cdot A'4}\) e quindi non dipende dalla scelta del punto 1 sulla circonferenza (Euclide, Elementi, Libro III, proposizione 37). Ne segue che ogni quadrangolo 1,2,3,4 inscritto nella circonferenza che abbia due lati opposti passanti per \(A \) e \(A'\) definisce sulla retta \(AA'\) la stessa involuzione. Se poi la retta \(AA'\) incontra la circonferenza nei punti \(D,D'\) allora si ha \( AD \cdot AD' = A1 \cdot A2\) e \( A'D \cdot A'D' = A'3 \cdot A'4\) (Euclide, Elementi, Libro III, proposizione 35) e quindi il rapporto tra i rettangoli \( \frac{AX' \cdot AX}{A'X' \cdot A'X} \) coincide con il rapporto \( \frac{AB \cdot AB'}{A'D \cdot A'D'}\) Dunque le coppie \( AA', XX', DD' \) fanno parte di una stessa involuzione. Poiché queste proprietà sono invarianti per proiezione, si ha che le stesse affermazioni restano valide se la circonferenza è sostituita da una qualunque conica che di questa è una proiezione.