 |
Curves on a quadric surfaceCurves on a smooth quadric surface.Let C be a curve of bidegree (a, b), a <= b, on a smooth quadric surface, Q. The exact sequence: 0 -> IQ -> IC -> IC,Q -> 0 reads like: 0 -> O(-2) -> IC -> OQ(-a,-b) -> 0 (*) Taking cohomology in (*), and using Künneth formula's: 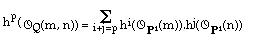 we get the whole cohomology of IC. For instance we see that every surface of degree n < b containing C is a multiple of Q (because h0(IC,Q(n)) = 0 if n < b) and that there are b-a+1 ("new") minimal generators in degree b. We also get that h1(IC(n)) = 0 for any n if a = b-1 or b (C is projectively normal); while, if b > a+1, h1(IC(n)) = 0 if n > b-2 and h1(IC(b-2)) = b-a-1 > 0. In the same way: h2(IC(n)) = 0 if n > a-2 and h2(IC(a-2)) = b-a+1 > 0 If a = b, C is a complete intersection (2, a) (C is contained in Q.F where F is the "new" generator of degree a, and C has degree 2a). If a < b, I(C) is generated by its elements of degree <= b (Castelnuovo-Mumford's lemma): so I(C) is generated by Q and by b-a+1 elements of degree b. If a = b-1, C is projectively normal and we easily see that the minimal free resolution is: 0 -> 2.O(-b-1) -> 2.O(-b) + O(-2) -> IC -> 0 From now on assume b > a+1. The minimal free resolution of I(C) looks like: 0 -> + S(-n3i) -> + S(-n2i) -> (b-a+1).S(-b) + S(-2) -> I(C)-> 0 Let c be the index of completness of C: c := max{n / h1(IC(n)) > 0}
We have c = b-2. It follows (Generalities on minimal free resolutions) that n3+ = b+2 (where n3+ := max{n3i}). Let e be the index of completness of C: e := max{n / h2(IC(n)) > 0}
We have e = a-2. Since c > e, it follows that: n3+ > n2+ > n1+ (where ni+ := maxj{nij}). Hence: b+2 = n3+ > n2+ > b. It follows that n2+ = b+1. On the other hand we also have: n3- > n2- > n1- In our case it is clear that n2- > b (a minimal relation among the generators has to involve a generator of degree b). It follows that: n2i = b+1, all i; and n3i = b+2, all i.Moreover since h1(IC(b-2)) = b-a-1 we have #{i / n3i = b+2} = b-a-1
Summarizing the minimal free resolution has the following shape: 0 -> (b-a-1).S(-b-2) -> x.S(-b-1) -> (b-a+1).S(-b) + S(-2) -> I(C) -> 0 Counting ranks we get x = 2(b-a). We conclude that the minimal free resolution of a curve of bidegree (a, b), b > a+1, on a smooth quadric is: 0 -> (b-a-1).S(-b-2) -> 2(b-a).S(-b-1) -> (b-a+1).S(-b) + S(-2) -> I(C) -> 0 Curves on a quadric coneLet C be a curve of degree d on a quadric cone, Q. If d is even then C is a complete intersection of type (2, d/2). The minimal free resolution of I(C) is: 0 -> S(-(d+4)/2) -> S(-d/2) + S(-2) -> I(C) -> 0 If d is odd then C is linked to a line in a complete intersection of type (2, (d+1)/2); C is projectively normal and the minimal free resolution of I(C) is: 0 -> 2.S(-(d+3)/2) -> 2.S(-(d+1)/2) + S(-2) -> I(C) -> 0 These can be seen as special cases of curves on a smooth quadric surface (curves of type (a, a) with a = d/2; or curves of type (a, a+1) with a = (d-1)/2). To prove this, one may argue, for example, as follows: Step 1: compute the genus of a curve on a quadric cone. Step 2: compute the virtual genus (=genus of the generic plane
section =: g(C.H)). Check that g(C) = g(C.H), this implies that the curve
is projectively normal. It follows that the minimal free resolution is
given by the minimal free resolution of the generic plane section. Step 3: Determine the minimal free resolution of d points on a smooth conic, and conclude. The most difficult is Step 1; for this you can work on a smooth model of the cone (the surface F2); or projecting from a general point of the cone you get a plane curve with only one singular point of multiplicity m (m = d/2 or (d+1)/2) and one principal tangent. After one blowing-up you get a curve with an ordinary m-fold point. You get a smooth curve by blowing-up once again. To compute the genus use ??. |