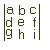
Una matrice (3x3), M, è una tabella, con 3 righe e 3 colonne, di numeri:
M=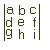
dove a, b,...,i sono numeri reali (che vengono chiamati i coefficienti di M).
Osserviamo che possiamo "stendere" la matrice: M = (a, b, c, d, e, f, g, h, i). Quindi, avendo fissato un ordine una volta per tutte (qui abbiamo scritto prima gli elementi della prima riga, poi della seconda riga, ...), darsi una matrice è equivalente a darsi 9 numeri in quel ordine (una 9-upla di numeri).
La matrice M è magica se le somme dei coefficienti su tutte le righe, tutte le colonne e su le due diagonali sono tutte uguali ad uno stesso numero:
a+b+c = s
d+e+f = s
g+h+i = s
a+d+g = s
b+e+f = s
c+f+i = s
a+e+i = s
c+e+g = s
In questo caso si dice che M è magica di somma s.
Per esempio la matrice nulla (la matrice i cui
coefficienti sono tutti nulli) è magica di somma 0; mentre la matrice, U (come uno), i
cui coefficienti sono tutti uguali a 1 è magica di somma 3.Più generalmente si può
definire la moltiplicazione di una matrice M per un numero x: se M = (a,b,c,d,e,f,g,h,i),
allora xM è la matrice (xa, xb, xc, xd,xe,xf,xg,xh,xi). Quindi xU = 
; chiaramente xU è magica, di somma 3x.Ecco un esempio un pò meno banale:
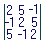;questa matrice è magica di somma 6.
Per vedere che ci sono tante altre matrici magiche ecco due giochini, uno difficile, l'altro un pò meno sulle matrici magiche:
Giochino meno difficile:
Quando si preme "Inizia", il computer crea (in modo casuale) una matrice magica ma ne visualizza solo una parte: gli elementi della prima diagonale sono riempizzati da lettere; il gioco consiste nell'indovinare questi elementi mancanti.Inserite i vostri tentativi nei campi testo e premete "Submit". Se rimanete bloccati potete chiedere un aiuto: premendo su "Somma" viene visualizzata la somma della matrice magica (a questo punto il gioco diventa banale); se proprio ancora non ce la fate, premendo su "Soluzione" si vede la soluzione.
Gioco più difficile:
Questa volta quando si preme "Inizia", il computer crea una matrice magica (in modo casuale), mescola i suoi coefficienti (in modo casuale) e visualizza il risultato. Il gioco consiste nel rimettere a posto i coefficienti di modo che la matrice sia magica. Si possono scambiare due coefficienti: basta cliccare su i relativi coefficienti per selezionarli (diventono rosa) e premere "Scambia"; si può avere un aiuto premendo "Somma"; quando si è stufi "Soluzione" fornisce una soluzione (la soluzione non è necessariamente unica). Le cifre in blu sono le somme delle varie righe, colonne e diagonali.
Chiaramente dietro questi giochini c'è della matematica;
chi è curioso di vedere come si fa a determinare tutte le matrici magiche
segua il link