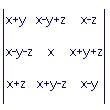 dove x,y,z sono numeri reali.
dove x,y,z sono numeri reali. Scopo di quanto segue è di dimostrare che ogni matrice magica, M, è della forma:
M = 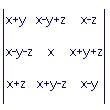 dove x,y,z sono numeri reali.
dove x,y,z sono numeri reali.
La dimostrazione qui proposta usa il seguente fatto: ogni matrice si scrive, in modo unico, come somma di una matrice simmetrica e di una matrice antisimmetrica.
Una matrice, S, è simmetrica se i suoi
elementi simmetrici rispetto alla diagonale principale sono uguali. La generica matrice
simmetrica è della forma S =  (Vediamo così
che le matrici simmetriche dipendono da 6 parametri: a,b,c,d,e,f).
(Vediamo così
che le matrici simmetriche dipendono da 6 parametri: a,b,c,d,e,f).
Una matrice A è antisimmetrica se gli
elementi sulla diagonale principale sono nulli e se quelli simmetrici rispetto alla
diagonale sono opposti. La generica matrice antisimmetrica è della forma A = .(Le matrici antisimmetriche dipendono da 3 parametri: u,v,w).
.(Le matrici antisimmetriche dipendono da 3 parametri: u,v,w).
Sia M = 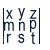 una matrice qualsiasi, se vogliamo scrivere M = S + A con S
simmetrica, A antisimmetrica, allora chiaramente a = x, b = n, c = t. Per gli altri
elementi dobbiamo avere, per esempio: d+u = y e d-u = m. Sommando le due equazioni: d =
(m+y)/2; invece sotraendo la seconda dalla prima u = (y-m)/2. Nello stesso modo e =
(z+r)/2, v=(z-r)/2 e finalmente f = (p+s)/2, w = (p-s)/2. Viceversa se M è somma di una
matrice simmetrica S' e di una matrice antisimmetrica A', è chiaro che deve essere S = S'
e A = A'. Questo dimostra che ogni matrice si scrive in modo unico come somma di una
matrice simmetrica e di una matrice antisimmetrica.
una matrice qualsiasi, se vogliamo scrivere M = S + A con S
simmetrica, A antisimmetrica, allora chiaramente a = x, b = n, c = t. Per gli altri
elementi dobbiamo avere, per esempio: d+u = y e d-u = m. Sommando le due equazioni: d =
(m+y)/2; invece sotraendo la seconda dalla prima u = (y-m)/2. Nello stesso modo e =
(z+r)/2, v=(z-r)/2 e finalmente f = (p+s)/2, w = (p-s)/2. Viceversa se M è somma di una
matrice simmetrica S' e di una matrice antisimmetrica A', è chiaro che deve essere S = S'
e A = A'. Questo dimostra che ogni matrice si scrive in modo unico come somma di una
matrice simmetrica e di una matrice antisimmetrica.
Sia M una matrice magica, di somma s, allora M, come ogni matrice, si scrive M = S + A dove S è simmetrica e dove A è antisimmetrica. Il fatto notevole è che anche S e A sono magiche.
Infatti, con le notazioni precedenti,verifichiamo che S è magica. Somma della prima riga: a+d+e = x + (m+y)/2 + (z+r)/2. Siccome M è magica: x+m+r = s, cioè (m+r)/2 = (s-x)/2 e x+y+z = s. Quindi a+d+e = (x+y+z)/2+(x+m+r)/2= s. Le altre verifiche si fanno nello stesso modo.
Per quanto riguarda A (se è magica la sua somma è 0:guardare la diagonale); somma della prima riga: u+v = (y-m)/2 + (z-r)/2. Ma, siccome M è magica: (y+z)/2 = (s-x)/2 = (m+r)/2. Quindi u+v=0. Le altre verifiche sono similari.
In conclusione: per determinare tutte le matrici magiche, basta determinare tutte le matrici magiche simmetriche e tutte le matrici magiche antisimmetriche. (Abbiamo spezzato il nostro problema in due problemi più semplici.)
Matrici magiche antisimmetriche.
E' il caso più facile. Con le notazioni precedenti se A antisimmetrica è magica, allora è magica di somma 0 e dobbiamo avere:
u+v = 0
-u+w = 0
v+w = 0
Si ricava facilmente: v = -u, w = u. Quindi A = 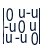 = u
= u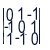 = u.A (dove
abbiamo posto A =
= u.A (dove
abbiamo posto A = 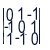 ). In
particolare le matrici magiche antisimmetriche dipendono da 1 parametro.
). In
particolare le matrici magiche antisimmetriche dipendono da 1 parametro.
Matrici magiche simmetriche di somma zero.
Per quanto riguarda le matrici magiche simmetriche inizieremo con un caso semplice: quello in cui la somma è zero. Con le notazioni precedenti dobbiamo avere:
(1) a+d+e=0
(2) d+b+f=0
(3) e+f+c=0
(4) a+b+c=0
(5) 2e+b=0
Da (5): e = -b/2 (*). Da (4): a = -b-c, inserendo in (1):
-c+d = -e+b = 3b/2 (**). Da (3): f = -e-c, inserendo in (2): d-c = e-b = -3b/2;
confrontando con (**), viene b = 0, e poi e=0, d=c=-a=-f. In conclusione S = a = a.S (dove abbiamo posto
S =
= a.S (dove abbiamo posto
S =  ). Quindi
anche le matrici magiche simmetriche di somma zero dipendono da un parametro.
). Quindi
anche le matrici magiche simmetriche di somma zero dipendono da un parametro.
Matrici magiche simmetriche.
Sia M una matrice magica simmetrica di somma s. La matrice N =(s/3)U (tutti i coefficienti uguali a s/3) è magica di somma s e simmetrica. Sia M' = M - N, si verifica facilmente che M' è magica, simmetrica e di somma 0. Per il punto precedente, M' è della forma a.S. Pertanto M = N + aS = (s/3)U + aS. In conclusione: ogni matrice magica simmetrica è della forma aS + bU (le matrici magiche simmetriche dipendono da due parametri).
Tutte le matrici magiche.
Mettendo tutto insieme, abbiamo: se M è magica, M si scrive (in modo unico) nella forma: M = xU + yS + zA; in altri termini, la generica matrice magica è della forma:
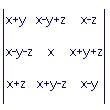
In particolare le matrici magiche dipendono da 3 parametri.
Osservazioni:
Per darsi una matrice magica casuale basta prendere x,y,z casuali e combinarli come sopra.
La somma è 3x, quindi il termine centrale è sempre (s/3).
Il termine centrale è la somma, divisa due, degli altri due termini sulla seconda diagonale (x = [(x+z)+(x-z)]/2); con questo accorgimento, il primo gioco diventa banale.
L'idea di questa dimostrazione viene dalla pratica dell'algebra lineare (l'insieme, M, delle matrici magiche è un sottospazio vettoriale di dimensione 3 dello spazio vettoriale, di dimensione 9, di tutte le matrici. C'è un piccolo miracolo: M è la somma diretta di Ma e Ms dove Ma (risp. Ms) è l'intersezione di M con il sottospazio delle matrici antisimmetriche (risp. simmetriche)). Una dimostrazione alternativa (meno elegante) si può fare con la teoria dei sistemi lineari.