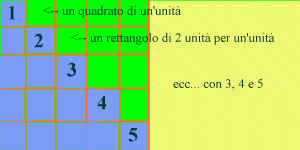
 i numeri sono rappresentati da striscioline rettangolari.
i numeri sono rappresentati da striscioline rettangolari.La teoria dei numeri ossia lo studio delle proprietà dei numeri naturali (i.e. 0,1,2,3,..) è iniziata con gli antichi Greci: Pitagora (-500), Euclide (-300), Diofante (150). Gli antichi Greci non disponevano del nostro sistema di numerazione, per loro i numeri avevano un supporto geometrico. Per esempio 52 era il numero di punti in un quadrato di lato 5 punti. Malgrado questo handicap notevole gli antichi Greci hanno ottenuto risultati importanti.
Ecco per esempio come stabilivano la formula 1+2+3+...+n = n(n+1)/2, la quale per n = 100 fornisce: 1+2+3+...+100 = 5050 (questa era, si pensa, quello che avrebbe detto Buttner)
Nel caso di 1+2+3+4+5:
 i numeri sono rappresentati da striscioline rettangolari.
i numeri sono rappresentati da striscioline rettangolari.
La somma 1+2+3+4+5 è rappresentata da un triangolo (in blu).
Dopodichè:
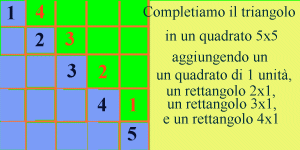
si completa con le striscioline verdi per ottenere
un quadrato di lato 5. Vediamo così che (1+2+3+4+5) + (1+2+3+4) = 52.
Questa costruzione è assolutamente generale:
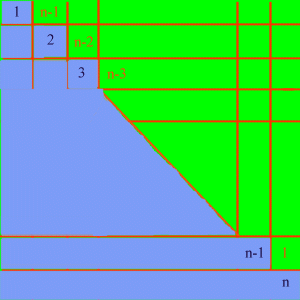
Quindi se Sn = (1+2+3+...+n), abbiamo:
Sn + Sn-1 = n2.
Aggiungendo n ad ambo i membri:
Sn + Sn-1 + n = n2 + n.
ma Sn-1 + n = (1+2+3+...+(n-1)) + n = Sn.
Quindi 2.Sn = n2 + n;
pertanto Sn = (n2 + n)/2, e la formula è dimostrata.
L'idea del giovane Gauss per calcolare 1+2+3+...+100, invece funziona così:
si osserva che i numeri fino a 100 possono essere accopiati simmetricamente rispetto a 50 con somma uguale a 100:
0 + 100 = 100
1 + 99 = 100
2 + 98 = 100
......................
48 + 52 = 100
49 + 51 = 100
Abbiamo 50 coppie di somma 100, per un totale di: 50 x 100 = 5000, e poi avanza 50, quindi 1+2+3+...+100 = 5050.
Elementare e molto elegante!
Seguendo quest'idea provate a dimostrare la formula generale 1+2+...+n = n(n+1)/2.