Cubiche piane
Una curva ellittica è in particolare una cubica piana, più precisamente una curva nonsingolare di grado tre nel piano proiettivo complesso. Cerchiamo di dare una vaga idea di questi termini.
Il piano proiettivo complesso: potete pensare al piano proiettivo come al piano usuale tranne che nel piano proiettivo due rette s'incontrano sempre in un punto (non esistono rette parallelle); "complesso" perchè invece di usare numeri reali per le coordinate dei punti, si usano numeri complessi. Il vantaggio è che una curva "ha sempre dei punti"! Per esempio la circonferenza x2+y2= -1 non ha punti nel piano (reale) usuale, invece ne ha nel piano complesso; sostanzialmente è lo stesso fenomeno per cui un'equazione del secondo grado può non avere soluzioni reali ma ha sempre due soluzioni complesse (x2 + 1 = 0 non ha soluzioni reali, le soluzioni complesse sono i e -i). In conclusione nel piano proiettivo complesso due rette s'intersecano sempre in un punto e tutte le curve hanno sempre dei punti, per il resto è come il piano normale. Il piano proiettivo complesso è ottenuto completando il piano usuale (reale) con punti "all'infinito" e punti a coordinate complesse, in particolare il piano proiettivo complesso contiene il piano usuale. Nel seguito abbrevieremo con "piano".
Cubica piana: è una curva definita da un'equazione polinomiale del terzo grado. Le curve più semplici sono le rette (equazioni del primo grado), poi vengono le coniche (per esempio le circonferenze) e dopo tocca alle cubiche. Per esempio (nel piano usuale, cioè reale) la curva di equazione y2 = x3 + 1 è una cubica.
Nonsingolare: la nostra cubica deve essere una curva "regolare", in ogni punto deve essere definita, in modo univoco, la sua tangente.
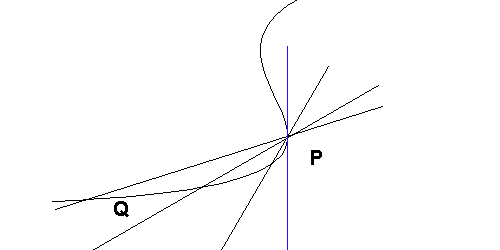
Quando il punto Q tende, lungo la curva, al punto P, la retta <Q,P> tende alla tangente (in blu) alla curva nel punto P.
La nostra curva non può avere "nodi" o altre singolarità.
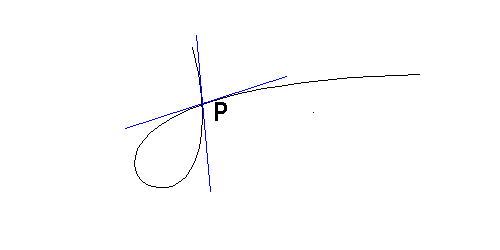
In questo caso la curva s'incroccia con se stessa; nel punto P abbiamo due tangenti. Il punto P è un punto singolare della curva (questo tipo di singolarità si chiama "nodo", ci sono altri tipi di singolarità)
La nostra curva non deve avere singolarità, si dice anche che la curva è liscia. Usando l'equazione, si può verificare, abbastanza facilmente, se la curva corrispondente è liscia.
Un'ultima cosa (fondamentale): nel piano (proiettivo) ogni retta interseca la nostra cubica in tre punti, contati con "molteplicità". Cosa significa "contati con molteplicità"? Abbiamo visto che la tangente in P è il limite delle secanti <P,Q> quando Q tende a P, la secante <P,Q> interseca la curva in due punti (P e Q), quindi al limite, nell'intersezione della tangente in P con la curva, il punto P deve essere contato due volte (la tangente "tocca" la curva). Ci sono quindi tre casi possibili:
Questa retta interseca la curva in tre punti distinti.
Questo è il caso generico. I casi seguenti riguardano le tangenti alla curva.
In generale una tangente farà un lavoro di questo tipo:
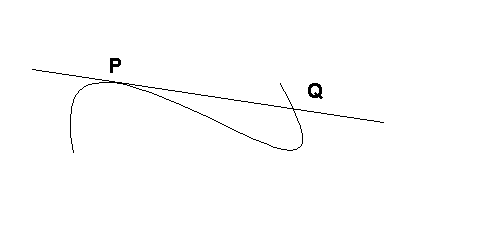La tangente in P incontra la curva in un altro punto, Q. L'intersezione
della tangente con la curva consta dei due punti P e Q. Però il punto P conta due volte
perchè la retta è tangente in P, mentre in Q è trasversale alla curva. Quindi contando
bene l'intersezione della retta con la curva "consta" ancora di "tre"
punti: due volte P e una volta Q.
Il caso più particolare è quello di una tangente di flesso:
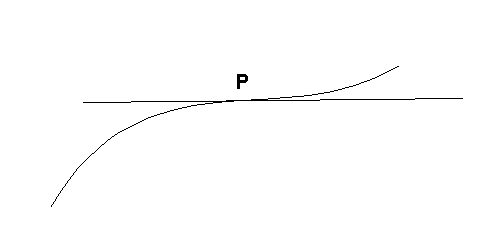Questo è un punto di flesso: la tangente
incontra la curva solo nel punto di tangenza. Contrariamente al caso precedente, questa
volta la curva "attraversa" la sua tangente; la tangente ha un contatto maggiore
con la curva. Contando bene, l'intersezione della tangente con la curva consta ancora di
tre punti: il punto P contato tre volte.
Si può dimostrare che una cubica ha esattamente 9 punti di flesso.
Adesso abbiamo tutto il necessario per definire l'addizione di due
punti sulla nostra curva, è ora di girare pagina! 