ProbleMATEMATICAmente - Novembre 2001

Soluzione proposta da: Giampiero Caruso, 4A, LS Boggio Lera, Catania  

RETTE INCIDENTI

Un caso particolare di rette incidenti sono le rette perpendicolari. In tal caso il luogo coincide con l’insieme dei punti interni al quadrato i cui vertici giacciono sulle due perpendicolari e il cui lato è uguale a (fig.5).

Si dimostra infatti (fig.6) che PH+PK=AO (semidiagonale del quadrato):

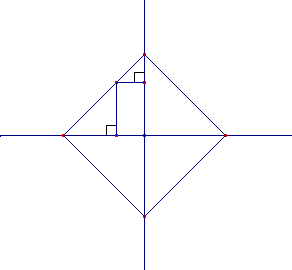
AO=AK+KO; essendo KO=PH (PKOH è un rettangolo) e AK=PK (il triangolo AKP è isoscele poiché rettangolo e perché l’angolo PAK=45°) sia ha che PH+PK=AO.
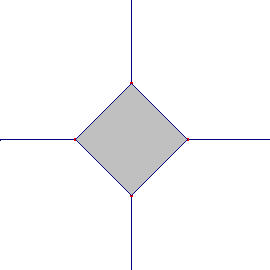
Ponendo AO=1 possiamo affermare che il perimetro di tale quadrato è il luogo dei punti P tali che la somma delle distanze di P dalle due rette sia uguale a 1, affinché possa essere anche minore di 1 i punti P devono essere pure interni al quadrato.

Più in generale possiamo descrivere tale luogo, per quanto riguarda rette incidenti generiche, con la seguente costruzione:

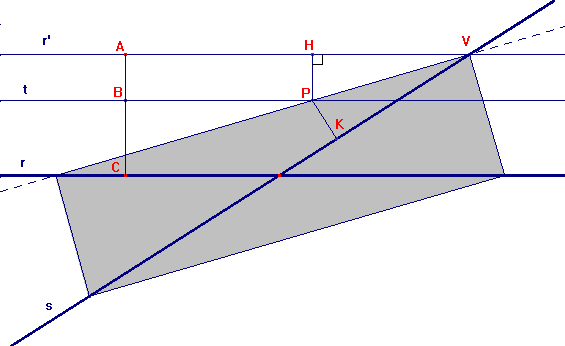
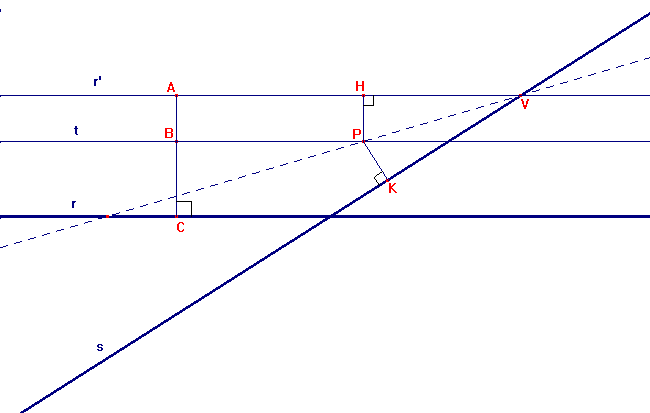
Tracciamo la retta r’ parallela ad r (fig.7) la cui distanza da quest’ultima sia uguale a 1 (AC=1). Stabiliamo arbitrariamente la distanza BC (con 0<BC<1) che P deve avere dalla retta r e costruiamo la retta t parallela ad r e passante per B.

Affinché BC+PK=1 dobbiamo porre PK=AB=HP, essendo AB+BC=AC=1. Affinché PK=HP il punto P deve appartenere alla bisettrice (luogo dei punti equidistanti da due rette: r’ ed s) dell’angolo HVK.
Notiamo quindi che qualunque sia la distanza BC che P ha dalla retta r, il punto P giace sulla bisettrice dell’angolo HVK.

Estendendo questo tipo di costruzione anche alla retta s e considerando che ciascuna delle rette r ed s ha due possibili rette parallele la cui distanza è 1, possiamo definire il luogo dei punti P tali che la somma delle distanze di P dalle due rette sia minore o uguale a 1 come l’insieme dei punti interni al rettangolo i cui vertici sono ottenuti dall’intersezione delle rette r ed s rispettivamente con le rette parallele ad s ed r la cui distanza da quest’ultime sia uguale a 1.

| Torna al Commento |