ProbleMATEMATICAmente - Maggio 2001

Soluzione proposta da Daniele Urzì, classe III B, liceo scientifico "G.Galilei" (Catania)

COMMENTO:

Il messaggio di Daniele Urzì conteneva alcune considerazioni che ci sembra importante riportare prima di proporre la sua soluzione:

"... la parte inversa è quella che mi ha creato maggiori difficoltà. Infatti in nessun modo riuscivo a dimostrare la seconda parte considerando valida la proprietà per un solo punto P. Poi ho capito che questo dipendeva dal fatto che esistono infiniti triangoli ABC non equilateri per i quali la proprietà è vera per un punto P del loro circocerchio e solo supponendo che essa sia valida per almeno due punti P il triangolo ABC è equilatero. Io mi sono limitato a costruire uno di quei triangoli non equilateri, forse sarebbe stato meglio   dimostrare se, dato un triangolo ABC e la circonferenza a esso circoscritta, esiste sempre un punto P dell'arco AB tale che PA + PB = PC. Ma questo è il testo di un nuovo problema..."

 La soluzione proposta:

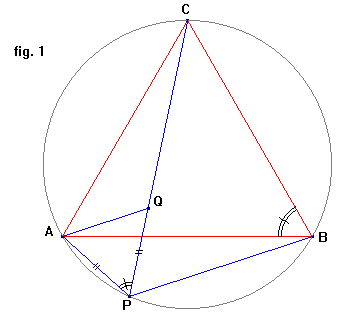
Sia Q un punto di PC tale che PQ=PA (fig.1). Il triangolo isoscele APQ è anche equilatero perché l’angolo APC misura 60° essendo uguale all’angolo ABC (insistono sulla stessa corda AC). Gli angoli ACP, ABP sono uguali perché insistono sulla stessa corda AP, mentre gli angoli AQC, APB sono uguali perché rispettivamente supplementari degli angoli di 60° AQP e ACB. Da queste considerazioni segue che i triangoli AQC e APB sono uguali, per cui è PB=CQ. E’ così dimostrato che PA+PB=PQ+CQ=PC, per qualunque punto P dell’arco AB. 

1. Se P coincide con A o con B la tesi è ovvia.
2. La dimostrazione è analoga se il punto Q è tale che PQ=PB.
3. Si noti che PQ è sempre contenuto nel segmento PC: rispetto al triangolo PAC, l’angolo ACP opposto al lato AP=PQ è sempre minore dell’angolo PAC opposto a PC. Infatti variando P sull’arco AB è sempre vera la relazione PAC=BAC+PAB=ACB+PCB>ACP (discorso analogo, rispetto al triangolo PBC, se è PQ=PB).

Adesso, dato un triangolo equilatero ABC e la circonferenza t di centro O e raggio r ad esso circoscritta, sia P un punto dell’arco AB diverso da A, da B e dall’altro estremo del diametro passante per C (fig.2). Facendo centro in P e con raggio uguale a PC si tracci una circonferenza v.
Essa è secante alla circonferenza t perché la distanza dei centri è minore della somma dei raggi e maggiore della loro differenza. Infatti, rispetto al triangolo PCO si hanno le relazioni PO<PC+r e PO>PC-r. Le due circonferenze hanno così due punti C e C’ in comune: essi sono distinti essendo t e v secanti, per cui il triangolo ABC’ non è equilatero, tuttavia essendo PC=PC’ è vera la relazione PA+PB=PC’.
Facendo variare P sull’arco AB si ottengono infiniti triangoli ABC’ non equilateri (se P coincide con l’altro estremo del diametro passante per C, t e v sono tangenti, per cui ABC’ coincide con ABC; mentre se P coincide con A o con B , C’ coincide con B o con A e il triangolo ABC’ degenera in un segmento).
In definitiva possiamo costruire infiniti triangoli ABC’ non equilateri per i quali esiste un punto P dell’arco AB del circocerchio tale che PA+PB=PC’. (1)

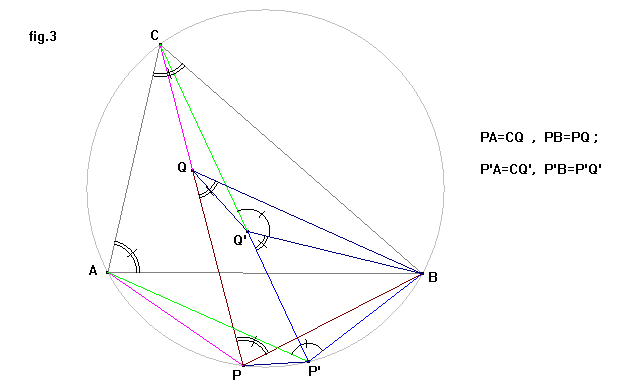
Invece, se la (1) è verificata per almeno due punti P distinti, ABC’ è un triangolo equilatero. Lo dimostriamo: supponiamo che dati due punti P e P’ dell’arco AB del circocerchio di un qualsiasi triangolo ABC, sia PA+PB=PC e P’A+P’B=P’C. Siano Q e Q’ due punti rispettivamente di PC e PC’ per i quali è PQ=PB e P’Q’=P’B (fig.3).
I triangoli PQB e P’BQ’ hanno gli angoli QPB e Q’P’B uguali perché insistono sulla stessa corda CB. Siccome sono isosceli, anche gli angoli alla base sono uguali, quindi i due triangoli sono simili: PB/P’B=QB/Q’B (1).
Essendo QBP=Q’BP’, gli angoli QBQ’ e PBP’ sono uguali perché differenze di angoli uguali con lo stesso angolo PBQ’ e per la (1) segue che i triangoli QBQ’ e PBP’ sono simili. Per cui è QQ’B=PP’B. E’ facile dimostrare che i triangoli CQQ’ e APP’ sono uguali. Essendo gli angoli CQ’Q, AP’P uguali, segue CQ’B=AP’B=APB. Gli angoli ACB, P’Q’B sono uguali perché supplementari degli angoli rispettivamente APB, CQ’B, uguali fra loro (ACB=P’Q’B=PQB).
I triangoli CQB, APB sono uguali (CQ=AP , PAB=PCB perché insistono sulla stessa corda PB, CQB=APB perché supplementari di PQB=ACB). Da ciò AB=CB per cui BCA=CAB=QPB. Essendo PQB=QBP=ACB=CPB, segue che il triangolo PQB è equilatero, quindi l’angolo CAB misura 60°. Il triangolo ACB è isoscele, un angolo interno è di 60°, allora ACB è un triangolo equilatero. Ed è ciò che volevamo dimostrare.

| Torna al Commento |