
ProbleMATEMATICAmente - Maggio 2001
Soluzione proposta da: Sandro Campigotto
PRIMA PARTE:

Ipotesi:
ABC triangolo equilatero,
P punto qualsiasi
dell’arco AB della circonferenza
circoscritta.
Tesi
![]()
Dimostrazione:
Sia x l’angolo ![]() e sia 2r il diametro della circonferenza circoscritta.
e sia 2r il diametro della circonferenza circoscritta.
Per il teorema della corda, posso calcolare:
![]() ,
,
![]() sfruttando
l’angolo
sfruttando
l’angolo ![]()
![]() (NOTA BENE: nella formula precedente c'è un refuso. Al posto di 2/3 va
letto 1/3)
(NOTA BENE: nella formula precedente c'è un refuso. Al posto di 2/3 va
letto 1/3)
sfruttando l’angolo ![]() ,
infatti
,
infatti ![]() è congruente a
è congruente a ![]() .
.
Possiamo quindi calcolare:
 ,
,
d’altra parte
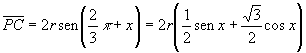 ,
,
quindi ![]() è verificata
per ogni possibile scelta di
è verificata
per ogni possibile scelta di ![]() .
.
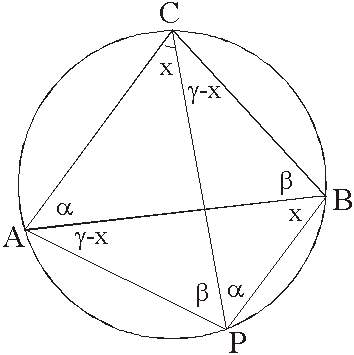
SECONDA PARTE
![]()
Tesi
Il triangolo ABC è equilatero.
Dimostrazione:
Siano ![]() ,
, ![]() e
e ![]() gli angoli del triangolo
gli angoli del triangolo ![]() , sia
, sia
![]() un punto dell’arco
un punto dell’arco ![]() e sia x l’angolo
e sia x l’angolo ![]() .
.
Per il teorema della corda posso scrivere che:
![]() ,
,
![]()
![]()
Risulta quindi che:
![]()
![]() , semplificando:
, semplificando:
![]()
Devo quindi verificare che l’equazione sopra riportata sia
verificata per ogni scelta di ![]() .
.
Eseguendo due calcoli con le formule trigonometriche:
![]() ,
,
raccogliendo:
![]() .
.
Dovendo essere verificata per ogni ![]() , deve accadere che:
, deve accadere che:
![]()
cioè:
![]()
elevando al quadrato la seconda equazione, ottengo il sistema:
![]()
Il sistema, se ha soluzioni, contiene anche le soluzioni del sistema precedente.
Risolvendo si ottiene che
![]()
che ha come unica soluzione ammissibile (![]() ),
),
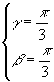
Quindi il triangolo ![]() è
equilatero.
è
equilatero.