ProbleMATEMATICAmente - Febbraio 2001

Soluzione proposta da:  Classe 3A programmatori, ITG Ruffini, Imperia

Abbiamo inizialmente verificato la disuguaglianza

+  

per via algebrica, elevando entrambi i membri al quadrato, senza porre ovviamente condizioni per la realtà , essendo tutti i radicandi maggiori di zero. Abbiamo ottenuto:

1+x²+1+y²+24+ x² +y² +2xy, da cui: 22+2xy

e poi :

a) nel caso 1+xy0 vera;

b) nel caso 1+xy>0, elevando al quadrato: (1+x²)(1+y²)1+x²y²+2xy e ancora 1+x²y²+ x²+y²1+x²y²+2xy ossia x²+y²-2xy0 cioè (x-y)²0.
L'uguaglianza è vera per x=y; in tutti gli altri casi è vera la disuguaglianza stretta.

Abbiamo tentato, per via algebrica¸di rispondere agli altri quesiti, ma i calcoli troppo lunghi ci hanno fatto capire che doveva esistere una via più breve.

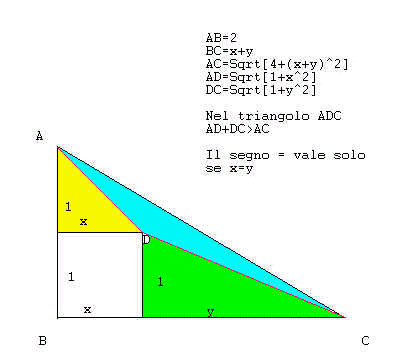
Abbiamo utilizzato la geometria, riportando le figure in due file di "Cabri" che alleghiamo e spieghiamo:

1. La prima consente di verificare la disuguaglianza facendo ricorso al teorema di Pitagora e precisamente

= ; = ; = .

Grazie al teorema per cui in un triangolo ogni lato è minore della somma degli altri due, si ha +

2. La seconda consente di estendere la disuguaglianza al caso di tre radicali e precisamente:

+ + + .

È evidente che nel caso di quattro radicali si avrà la disuguaglianza:

+ + +

| Torna al Commento |