ProbleMATEMATICAmente - Dicembre 2000
Soluzione proposta da: Nallin Laura, III B - L.S. Statale "G. Galilei", Adria, (RO)

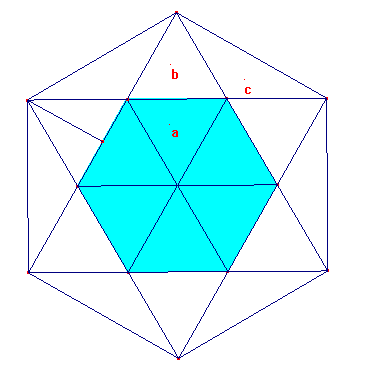
I triangoli "a" sono tutti isometrici tra loro e sono equilateri (ciò si capisce anche dalla costruzione), sono isometrici ai triangoli "b" tra loro isometrici (equilateri per costruzione).
I triangoli "c" sono tra loro isometrici per il primo criterio d’isometria, hanno isometrici i due lati isometrici (essendo isosceli) che sono i prolungamenti dell’esagono iniziale e l’angolo tra questi compreso che è l’opposto dell’angolo interno dell’esagono.
Quindi l’esagono ottenuto ha tutti i lati isometrici.
Per la somma di angoli isometrici possiamo dire che tale esagono è anche equiangolo, poiché i suoi angoli sono la somma dei due angoli di base dei triangoli isosceli "c" e di un angolo del triangolo equilatero "b".
Concludendo, la figura trovata prolungando i lati dell’esagono iniziale è un esagono regolare.
Valutando la coppia dei triangoli "b", "c" posso affermare che sono equiscomponibili poiché hanno ugual base e uguale altezza; quindi il triangolo "c" è equiscomponibile al triangolo "b" che è equiscomponibile al triangolo "a", hanno tutti area 1/6, allora l’esagono ottenuto ha area 3.
NOTA: per chi non fosse abituato, la parola "equiscomponibile" va intesa come "equivalente", cioè con la stessa area.