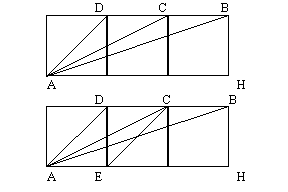
Soluzione di Musiani e Minguzzi

I° SOLUZIONE
Tesi--> a+b=45° (CAH+BAH=45° cioè CAH+BAH=DAH);
La tesi è verificata per DAC=BAH infatti DAC+CAH=DAH se DAC=BAH la tesi è dimostrata.
Si indicherà con l la lunghezza del lato di ciascun quadrato e con rad il simbolo di radice quadrata.
PROCEDIMENTO
Si traccia CE.CE=l*rad2.
CE interseca AB in O che è punto medio sia di CE che AB.
CO=(l*rad2)/2=l/rad2.
Si considerano i triangoli ADC e COB.
Tali triangoli sono simili per il criterio di similitudine. Infatti:
- DC:CO=AD:BC (essendo in valori numerici x:x/rad2=xrad2:x)
- ADC=OCB [angoli] (per identica costruzione)
Per le dovute corrispondenze risulta che DAC=OBC, ma OBC=BAH perché alterni interni quindi DAC=BAH.
La tesi è dimostrata.