Domizia Badodi – classe III A – Liceo scientifico Spallanzani di Reggio Emilia

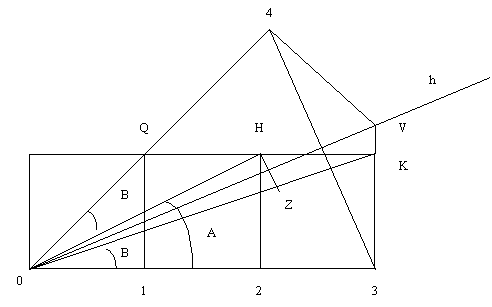
Si prende su OK, OZ » OH quindi OHZ isoscele (punto medio della base = bisettrice dell’angolo al vertice)
Si traccia l’altezza h
Si prolunga 3K fino ad h (V)
Si disegna il triangolo simmetrico a O3V rispetto ad OV (V4O) simile a O3V quindi 4O^V » VO^3 quindi 4O^3 » 2B + (A – B) = B + A
Il segmento 4O deve passare per Q : se non lo facesse, i triangoli 4OV e VO3 non sarebbero congruenti (condizione che ci ha fatto ricavare A+B)
Q è il vertice del 1° quadrato: OQ ne è dunque la diagonale, quindi la bisettrice degli angoli di 90° che risultano di 45° quindi QO^3 = A+B = 45°