ProbleMATEMATICAmente - Marzo 2000
Soluzione proposta da
Umberto Villa
3^I del LS "Vittorio Veneto" (MI)
Metodo 1
Consideriamo l’ellisse in un sistema di assi cartesiani ortonormali, avente come assi gli assi coordinati, la sua equazione in forma canonica Ŕ:
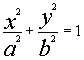
L’ellisse risulta diviso dagli assi cartesiani in 4 archi simmetrici. Consideriamo ora per comoditÓ solo la parte di ellisse contenuta nel primo quadrante (le osservazioni fatte su di essa varranno anche sulle altre parti di essa).
Le coordinate di un punto di questo arco di ellisse saranno del tipo:
![]()
con 0 ú x0 │ a
Calcoliamo l’area del rettangolo individuato dai punti O(0;0), P0 e dalle proiezioni di tale punto sugli assi cartesiani:
![]()
Viene ora richiesto quando questa funzione Ŕ massima:
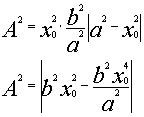
Sostituendo A2= t, x2 = z, otteniamo:
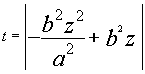
Questa Ŕ l’equazione di una parabola, quindi l’ordinata del suo vertice sarÓ il massimo reale:
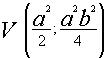
Ne consegue che l’area massima e il punto in questione sono:
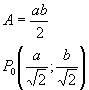
Considerando tutto l’ellisse, il rettangolo con area maggiore in esso inscritto sarÓ formato dai simmetrici di P0 rispetto agli assi cartesiani e alla loro origine, e avrÓ area 4A.
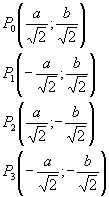
A=2ab
Metodo 2
Consideriamo l’ellisse in un sistema di assi cartesiani ortonormali, avente come assi gli assi coordinati, la sua equazione in forma canonica Ŕ:
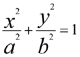
L’ellisse risulta diviso dagli assi cartesiani in 4 archi simmetrici. Consideriamo ora per comoditÓ solo la parte di ellisse contenuta nel primo quadrante (le osservazioni fatte su di essa varranno anche sulle altre parti di essa).
Immaginiamo di intersecare questo arco di curva con un fascio di iperboli equilatere aventi per asintoti gli assi cartesiani:
![]()
dove k rappresenta l’area del rettangolo formato da O(0;0) dal punto dell’iperbole P(x;y) e dalle sue proiezioni sugli assi cartesiani.
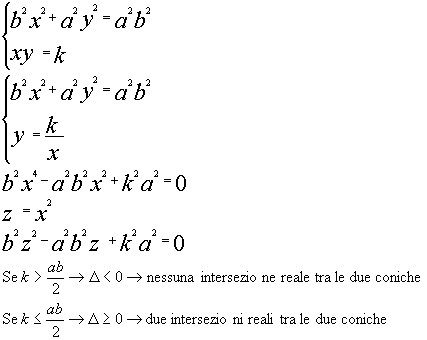
Rappresenta il valore limite per il quale le due curve sono tangenti in un punto P0 e l’area del rettangolo di vertici O(0;0), P0 e le sue proiezioni sugli assi coordinati:
![]()
![]()
Considerando tutto l’ellisse, il rettangolo con area maggiore in esso inscritto sarÓ formato dai simmetrici di P0 rispetto agli assi cartesiani e alla loro origine, e avrÓ area 4A.
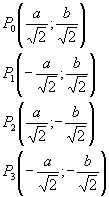
A=2ab