ProbleMATEMATICAmente - marzo 2000
Soluzione proposta da:
Jacopo Stoppa della 5^ sper.
LS "Galilei" di Adria
(RO)
Risolviamo dapprima il problema analogo sulla circonferenza di raggio r centrata nell’origine di un sistema di riferimento rettangolare. Consideriamo i raggi vettore dal centro della circonferenza ai vertici del quadrilatero inscritto. Chiamiamo
q1, q2, q3, q4 i quattro angoli compresi tra due raggi vettori adiacenti. L’area del quadrilatero è allora:
Essendo 0<=sen a<= 1, avremo sicuramente un massimo se sen q1 = sen q2 = sen q3 = sen q4 = 1, il che è possibile ed accade quando q1 = q2 = q3 = q4 = p/2.Allora le diagonali del nostro quadrilatero di area massima sono perpendicolari tra loro, il che implica che si tratta di uno degli infiniti quadrati inscritti nella circonferenza. L’area massima è 2r2.
Viene spontaneo pensare di applicare la stessa costruzione all’ellisse. Incontriamo però un problema in quanto il modulo dei raggi vettore non è costante (l’espressione esplicita si ricava dalle equazioni parametriche dell’ellisse), quindi l’espressione da minimizzare diventa più complessa.
Aggiriamo l’ostacolo osservando che ogni ellisse è l’immagine di una qualche circonferenza sotto un’affinità a.
Se la nostra ellisse centrata nell’origine O di un sistema di riferimento rettangolare ha semiasse maggiore a e semiasse minore b, possiamo prendere come "generatrice" ad esempio la circonferenza di centro O e raggio a con l’affinità
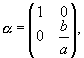
corrispondente a uno schiacciamento lungo l’asse y.
Sappiamo del resto che le affinità trasformano le aree di un fattore costante |D| , con D determinante della matrice della trasformazione, D(a) = b/a. Ne segue che il rapporto tra le aree delle figure è preservato dell’affinità; dunque i quadrilateri di area massima inscritti nell’ellisse sono le immagini dei quadrati inscritti nella circonferenza corrispondente (ad esempio il rombo con i vertici nelle intersezioni dell’ellisse con gli assi coordinati). L’area massima è 2a2 |D| = 2a2 (b/a) = 2ab.
I quadrilateri di area massima sono infiniti parallelogrammi equivalenti, ma ovviamente NON tutti i parallelogrammi inscritti hanno area massima!
Osserviamo per inciso che l’area
del quadrato inscritto nell’ellisse è 4a2b2/(a2+b2)
<= 2ab. Infatti
in quanto a, b > 0 e
per la disuguaglianza tra media geometrica e quadratica. L’uguaglianza vale solo se a = b, ovvero se l’ellisse degenera in una circonferenza.
Nota:
la matrice
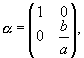
è un modo sintetico per scrivere la trasformazione
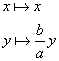
Questa trasformazione dilata l'area di tutte le figure di un fattore b/a. Quindi se l'area di un quadrato è A=2a2 allora l'area della sua immagine è (b/a)A=2ab. ( Torna al testo sopra )