Soluzione proposta da:
Ponti Giovanni
VH - Liceo Scientifico Statale di Rende "Pitagora"

Essendo l’ellisse simmetrica rispetto agli assi e al centro del riferimento cartesiano, mi limito a considerare soltanto il I quadrante e, in particolare, un punto P appartenente all’ellisse nel I quadrante stesso. Considerata l’ellisse di equazione , il punto P avrà coordinate . Per calcolare l’ordinata del punto, impongo la condizione di appartenenza all’ellisse e, poiché limito il mio studio solo al primo quadrante, l’ordinata sarà positiva. Il punto pertanto ha coordinate . Siano T e V le proiezioni del punto sugli assi cartesiani. Calcolo le distanze PV e PT:

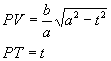
L’area del quadrilatero PTOV è :

A questo punto, calcolo la derivata prima di f(t) per determinare poi, studiando il segno di tale derivata, i punti in cui l’area del quadrilatero assume il suo massimo valore:

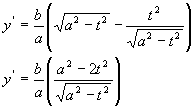
Studiamo ora il segno della derivata prima, analizzando quando N>0 e D>0. Nello studio del segno si possono omettere i valori di a e di b perché già maggiori di zero per ipotesi

(perché 0<t<a per il limite geometrico)

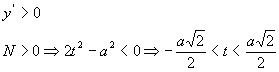
Da ciò si deduce che per la funzione assume il suo massimo valore. Quindi, il quadrilatero regolare di area massima inscritto nell’ellisse si ottiene prolungando i segmenti PV, PT e PO fino ad incontrare l’ellisse in altri tre punti e unendo i rispettivi anche con il punto P. Inoltre, il tipo di quadrilatero inscritto dipende dall’eccentricità della curva (, dove c è la distanza tra un fuoco e l’origine): nel caso particolare del cerchio e=0 ed il quadrilatero sarà un quadrato; nel caso più generale dell’ellisse 0<e<1 ed il quadrilatero sarà un rettangolo.

| Torna al commento |