Soluzione al problema di Aprile 2000 proposta da:
Jacopo
Stoppa - Liceo
Scientifico Statale G. Galilei - Adria,
(RO).
Il secondo problema implica la risoluzione, in interi positivi, dell’equazione
![]()
L’equazione equivale al sistema simmetrico, sempre da risolvere in N
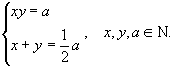
Come segue dal TEOREMA di RUFFINI, le soluzioni del sistema sono quelle dell’equazione di 2° grado
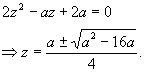
Accettiamo solo soluzioni in N; come prima cosa il radicando deve essere un quadrato perfetto:
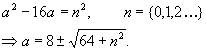
Ancora, deve essere
![]()
Abbiamo scelto k ed n >= 0 perché compaiono al quadrato e il segno è ininfluente sulle soluzioni.
Dovendo dunque essere k + n > k – n le uniche possibilità rimaste per esprimere 64 come prodotto di due fattori sono:
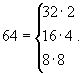
Risolvendo i corrispondenti sistemi lineari in k ed n otteniamo i "candidati"
![]()
Sostituendo successivamente i valori di n trovati abbiamo i "candidati" per a = 25, a = 18, a = 16. Le soluzioni corrispondenti sono le coppie non ordinate {x, y} = {10, 10/4}, {x, y} = {6, 3}, {x, y} = {4, 4}.
Le uniche soluzioni in interi sono dunque {6, 3} e {4, 4}.