FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema:

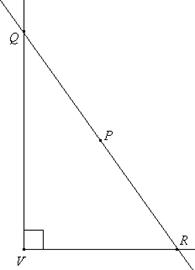
1) Dato un angolo retto di vertice V e un punto P interno ad esso, costruire la retta r passante per P tale che, detti Q e R i punti di intersezione di r con i lati dell’angolo, risulti .

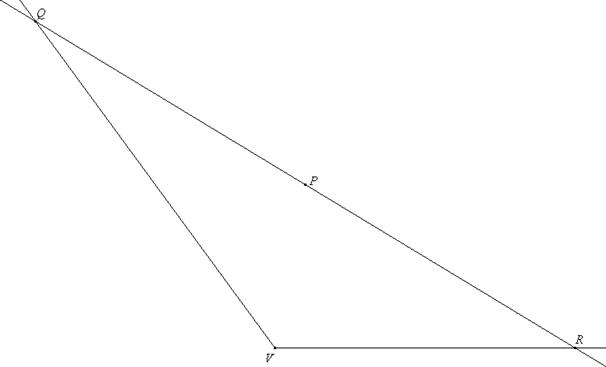
2) Dato un angolo di vertice V e minore di un angolo piatto, sia P un punto interno ad esso ed appartenente alla sua bisettrice. Costruire la retta r passante per P tale che, detti Q e R i punti di intersezione di r con i lati dell’angolo, risulti .

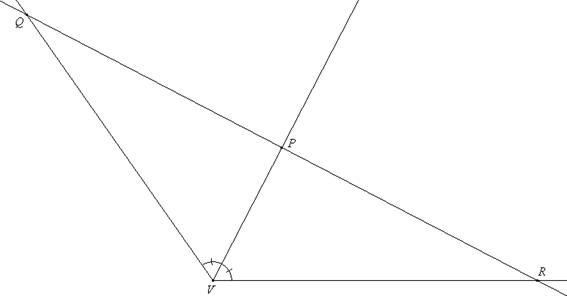
3) Dato un angolo di vertice V e minore di un angolo piatto, sia P un punto interno ad esso. Costruire la retta r passante per P tale che, detti Q e R i punti di intersezione di r con i lati dell’angolo, risulti .

Motivare tutte le costruzioni proposte.

Commento

Sono giunte otto risposte tutte da classi di Liceo Scientifico: cinque da una classe prima di un Liceo di Zurigo (Svizzera), due da due classi seconde di due diversi Licei e infine una da una classe terza.

Il problema poneva tre quesiti, di tipo costruttivo, con relativa motivazione. Nel primo quesito si chiedeva di costruire una retta passante per un punto generico interno a un angolo retto e soggetta a determinate condizioni; nel secondo di costruire una retta passante per un punto generico appartenente alla bisettrice di un dato angolo di ampiezza minore di un angolo piatto e di nuovo soggetta alla stessa condizione; nel terzo di costruire ancora una volta una retta passante per un punto generico interno a un angolo di ampiezza minore di un angolo piatto e sempre soggetta alla stessa condizione.

Rispondono correttamente ai quesiti gli studenti di seconda e terza Liceo, mentre non sono accettabili le risposte inviate dagli allievi della classe prima, perché spesso in esse vengono scambiate ipotesi e tesi, anzi a volte la dimostrazione si basa su una figura dove la tesi viene già utilizzata. Questo modo di procedere è abbastanza diffuso tra gli studenti che si cimentano per la prima volta nella dimostrazione di proprietà geometriche. È comunque apprezzabile il tentativo di arrivare alla proprietà richiesta attraverso “un ragionamento”.

Sono pervenute risposte dalle seguenti scuole:

LS “Don Milani”, Montichiari (BS)
LS “L. Cremona”, Milano
LS “P.M. Vermigli”, Zurigo (Svizzera)

Come di consueto presentiamo tutti i commenti riuniti in questo unico file PDF (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

| Home Page Cabri | Torna a FLATlandia | Archivi |