FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

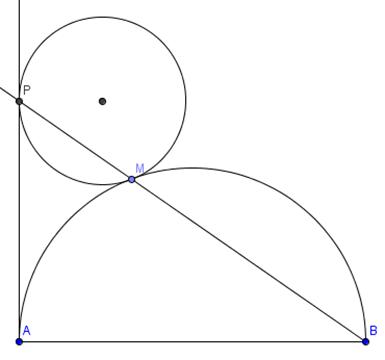
Il testo del problema

Sono date la semicirconferenza di diametro AB e la semiretta ad essa tangente in A. Preso un punto M sulla semicirconferenza si tracci la semiretta BM e sia P la sua intersezione con la tangente.

1)     Provare che .

2)     Costruire la circonferenza tangente in P alla semiretta AP e passante per M.

3)     Provare che tale circonferenza è tangente alla semicirconferenza iniziale.

Commento

Abbiamo ricevuto ventisette risposte così suddivise: una da una classe prima di Liceo Scientifico, diciotto da classi seconde e tre da classi terze, sempre di Scuole Superiori (con decisa prevalenza del Liceo Scientifico come tipologia di scuola); sono inoltre arrivate cinque risposte da classi di Scuola Media (più precisamente di Scuola Secondaria di I grado), facenti parte di due Istituti Comprensivi, tre da Classe seconda e due di Classi terze.

Il problema poneva tre domande (tra loro collegate) e riguardava inizialmente una figura geometrica costituita da una semicirconferenza e da due semirette, una tangente e l’altra secante, aventi come origine gli estremi del diametro della semicirconferenza: nel primo quesito si chiedeva di dimostrare l’esistenza di una data relazione tra le lunghezze di alcuni segmenti presenti nella figura iniziale; nel secondo si chiedeva di costruire una circonferenza con determinate caratteristiche e nel terzo quesito si chiedeva di dimostrare la tangenza tra la circonferenza costruita e la semicirconferenza iniziale.

Quasi tutti rispondono in modo sostanzialmente corretto alle prime due domande (anche se non mancano le imprecisioni), mentre, per quanto riguarda la terza domanda, pochissimi si mostrano in grado di effettuare correttamente la dimostrazione, probabilmente fuorviati da certe relazioni (come l’allineamento di certi punti o la concorrenza di certe rette) che la figura (costruita con un software di geometria dinamica) fa apparire come “evidenti” e che, invece, devono essere dimostrate.

È sempre presente l’abitudine a confondere un segmento con la sua lunghezza e un angolo con la sua ampiezza, con la conseguenza di utilizzare la stessa notazione per indicare due concetti diversi.

Sono pervenute risposte dalle seguenti scuole:

-        LS “G. Galilei”, Adria (RO)

-        LS “Alfano da Termoli”, Termoli (CB)

-        LS “Don Milani”, Montichiari (BS)

-        LS Scienze Applicate “B. Russell”, Cles (TN)

-        LS “Archimede”, sez. associata di Aci Bonaccorsi (CT)

-        LS “XXV Aprile”, Portogruaro (VE)

-        LS Linguistico “G. Ferraris”, Taranto (TA)

-        LS “Aristosseno”, Taranto (TA)

-        Istituto Comprensivo “G. Deledda”, Ginosa (TA)

-        Istituto Comprensivo “G. Deledda”, Pattada (SS).

 Come di consueto presentiamo tutti i commenti riuniti in questo unico file PDF (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

Il gruppo di lavoro che gestisce FLATlandia è composto da:

- Ercole CASTAGNOLA - NRD Università di Napoli “Federico II”
- Giuliano MAZZANTI - Docente di Geometria, Università di Ferrara
- Valter ROSELLI - Ricercatore, Dipartimento di Matematica, Università di Ferrara
- Luigi TOMASI - Insegnante di Matematica, LS "Galileo Galilei", Adria (RO)

| Home Page Cabri | Torna a FLATlandia | Archivi |