FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema

È dato un triangolo ABC avente per mediane i segmenti AE, BF e CD. Tracciare il segmento FH parallelo alla mediana AE e ad essa congruente. Tracciare poi il segmento FE e prolungarlo fino ad incontrare nel punto G il segmento BH (vedi figura).

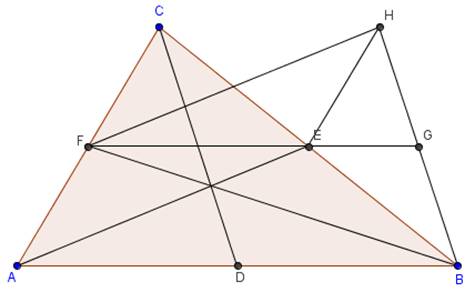
Dimostrare che:

a)     il quadrilatero AEHF ê un parallelogrammo;

b)     ;

c)     FG è una mediana del triangolo BFH;

d)     .

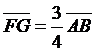Commento

Abbiamo ricevuto dodici risposte così suddivise: una risposta da una classe prima di Liceo Scientifico, quattro da classi seconde e una da una classe terza, sempre di Scuole Superiori (con decisa prevalenza del Liceo Scientifico come tipologia di Scuola); sono inoltre arrivate sei risposte da classi di Scuola Media (più precisamente di Scuola Secondaria di I grado) di cui cinque facenti parte di un Istituto Comprensivo, tutte di classi seconde e una di classe terza.

Il problema chiedeva innanzi tutto di tracciare, partendo da un dato triangolo con relative mediane, alcuni segmenti soddisfacenti certe proprietà specificate. Si chiedeva poi di dimostrare quattro diverse proprietà geometriche. Precisamente: a) che un quadrilatero, risultante dalla figura così ottenuta, fosse un parallelogramma; b) l’uguaglianza delle lunghezze, e quindi la congruenza, di due segmenti; c) che un segmento risultante dalla costruzione effettuata fosse una mediana di un triangolo facente parte della figura; d) la verifica di una particolare relazione tra le lunghezze di due segmenti.

In un buon numero di risposte pervenute il problema viene risolto in tutte le sue parti in modo sufficientemente corretto (salvo alcune imprecisioni nelle diverse dimostrazioni), mentre in alcune risposte non si fornisce un’adeguata motivazione della costruzione effettuata. Dobbiamo ancora una volta ribadire la necessità di distinguere tra un ente geometrico e la sua misura (in particolare tra un angolo e la misura della sua ampiezza e tra un segmento e la sua lunghezza).

Ci preme inoltre segnalare che alcuni studenti danno per scontata l’esistenza di certe relazioni (come l’allineamento di certi punti o il parallelismo di certe rette) che la figura (costruita con un software di geometria dinamica) fa apparire come “evidenti” e che, invece, devono essere dimostrate.

Infine è importante che gli studenti sappiano distinguere tra la definizione di parallelogramma, cioè di un quadrilatero che soddisfa determinate caratteristiche, e le condizioni sufficienti (o necessarie e sufficienti) che assicurano che un certo quadrilatero sia un parallelogramma.

Sono pervenute risposte dalle seguenti scuole:

LS “Don Milani”, Montichiari (BS)

LS “XXV Aprile”, Portogruaro (VE)

LS Linguistico “G. Ferraris”, Taranto

LS Scienze Applicate “B. Russell”, Cles (TN)

Ist. Sc. Stat. “A. Guarasci”, Soverato (CZ)

LS “Aristosseno”, Taranto

Ist. Comp. “G. Deledda”, Ginosa (TA)

Ist. Comp. “G. Deledda”, Pattada (SS)

SM “G.B. Tiepolo”, Milano

 Come di consueto presentiamo tutti i commenti riuniti in questo unico file PDF (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

Il gruppo di lavoro che gestisce FLATlandia è composto da:

- Ercole CASTAGNOLA - NRD Università di Napoli “Federico II”
- Giuliano MAZZANTI - Docente di Geometria, Università di Ferrara
- Valter ROSELLI - Ricercatore, Dipartimento di Matematica, Università di Ferrara
- Luigi TOMASI - Insegnante di Matematica, LS "Galileo Galilei", Adria (RO)

| Home Page Cabri | Torna a FLATlandia | Archivi |