FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema

Sia O il centro del quadrato BCDE costruito sull’ipotenusa di un triangolo rettangolo ABC (retto in A).

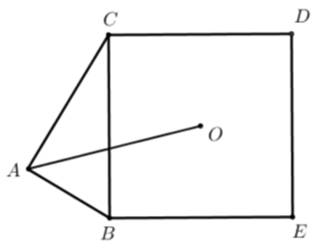
a) Dimostrare che AO biseca l’angolo BAC.

b) Prolungato il lato AB, dalla parte di B, di un segmento BF congruente ad AC, provare che ACEF è un trapezio.

c) Come deve essere scelto il triangolo rettangolo ABC affinché il trapezio suddetto sia equivalente al quadrato?

Commento

Abbiamo ricevuto diciassette risposte così suddivise: due da classi prime delle Scuole Superiori, sei da classi seconde e cinque da classi terze, sempre di Scuole Superiori (con decisa prevalenza del Liceo Scientifico come tipologia di scuola); ci sono state inoltre quattro risposte provenienti da classi seconde di Scuola Media, o, meglio, da quattro classi diverse (tutte seconde) di uno stesso Istituto Comprensivo.

Il problema riguardava una figura geometrica costituita inizialmente da un triangolo rettangolo e da un quadrato costruito sull’ipotenusa, esternamente al triangolo stesso, e poneva tre domande (tra loro collegate). Nel primo quesito si chiedeva di dimostrare che il segmento congiungente il vertice dell’angolo retto del triangolo col centro del quadrato era anche bisettrice dello stesso angolo retto; nel secondo si chiedeva di costruire, dopo aver opportunamente prolungato un lato del triangolo, un quadrilatero e di dimostrare che tale quadrilatero era un trapezio  e infine nel terzo quesito si chiedeva quali caratteristiche dovesse avere il triangolo rettangolo affinché il trapezio costruito fosse equivalente al quadrato.

Quasi tutti rispondono in modo sostanzialmente corretto alle prime due domande (anche se con alcune imprecisioni), mentre, per quanto riguarda la terza domanda, solo alcuni dimostrano che solo il triangolo rettangolo isoscele soddisfa alla richiesta equivalenza: la maggioranza (probabilmente per un uso non appropriato del software di geometria dinamica) suppone che il triangolo sia anche isoscele e dimostra di conseguenza l’equivalenza.

Dobbiamo sottolineare ancora una volta la presenza in quasi tutte le soluzioni di un “errore” (forse dovremmo dire un’imprecisione) abbastanza comune in tutti i livelli scolari, cioè confondere un segmento con la sua lunghezza e un angolo con la sua ampiezza, il che porta a utilizzare la stessa notazione per indicare due concetti diversi.

Sono pervenute risposte dalle seguenti scuole:

• LS “G. Galilei”, Adria (RO)

• LS “Alfano da Termoli”, Termoli (CB)

• LS “Don Milani”, Montichiari (BS)

• LS “R. Donatelli”, Terni (TR)

• LS Scienze Applicate “B. Russell”, Cles (TN)

• LS “XXV Aprile”, Portogruaro (VE)

• LS “Visitandine-Malpighi”, Castel San Pietro Terme (BO)

• ISIS “Archimede”, San Giovanni in Persiceto (BO)

• LS “G. Aselli”, Cremona (CR)

• LS “Aristosseno”, Taranto (TA)

• Ist. Comprensivo “G. Deledda”, Ginosa (TA)

Come di consueto presentiamo tutti i commenti riuniti in questo unico file PDF (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

| Home Page Cabri | Torna a FLATlandia | Archivi |