FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema

Nella figura sotto riportata è rappresentato un parallelepipedo rettangolo ABCDEFGH. L’angolo ÐDGH misura 45° e l’angolo ÐFGB misura 60°.

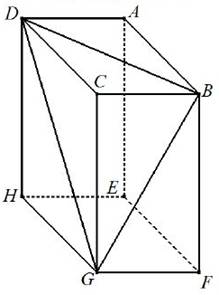
a) Di che tipo è il triangolo BDG?

b) Se lo spigolo BC ha lunghezza 1, quanto vale il volume della piramide DGCB?

c) Costruire con riga e compasso uno sviluppo piano della piramide DGCB.

d) Verificare che la somma dei quadrati delle aree delle facce della piramide DGCB che hanno un vertice in C è uguale al quadrato dell’area del triangolo BDG.

Commento

Abbiamo ricevuto diciassette risposte così suddivise: una da una classe prima di Liceo Scientifico, nove da classi seconde e due da classi terze, tutte di Licei Scientifici; inoltre cinque risposte provenienti da classi di Scuola Media (ossia Scuola Secondaria di I grado) facenti parte di due Istituti Comprensivi, quattro di classi terze e una di classe seconda.

Il problema poneva quattro domande (tutte relative alla stessa figura geometrica, cioè un parallelepipedo rettangolo): nel primo quesito si chiedeva di individuare la tipologia di un triangolo facente parte della figura iniziale; nel secondo si chiedeva di calcolare il volume di una piramide (sempre parte del parallelepipedo) dopo aver fissato come unità di misura la lunghezza di uno degli spigoli del parallelepipedo; nel terzo si chiedeva di costruire con riga e compasso lo sviluppo piano della piramide di cui era stato determinato il volume; infine nel quarto si chiedeva di verificare l’esistenza di una data relazione tra i quadrati delle aree delle facce sempre della stessa piramide.

Quasi tutti individuano la risposta corretta al primo quesito, ma manca da parte di alcuni la giustificazione di quanto affermato. La maggior parte calcola correttamente il volume della piramide, anche se non mancano errori e imprecisioni. Pochi forniscono la corretta motivazione della costruzione con riga e compasso dello sviluppo piano della piramide: ancora una volta ci si dimentica che le costruzioni tramite un software di geometria dinamica richiedono una giustificazione. Infine diversi sbagliano, per errori di calcolo o per mancanza di motivazioni, la verifica della relazione esistente tra i quadrati delle facce della piramide (peraltro abbastanza nota). Ribadiamo che una qualsiasi risposta, numerica o grafica o simbolica, in mancanza di opportune giustificazioni non sarà considerata corretta.

Osserviamo infine che in alcune risposte abbiamo rilevato una scarsa cura nel linguaggio utilizzato e nella scrittura delle formule, cosa che a volte sconfina nella sciatteria. Pertanto raccomandiamo caldamente a tutti gli studenti una attenta rilettura dell’elaborato prima dell’invio.

Sono pervenute risposte dalle seguenti scuole:

LS “G. Galilei”, Adria (RO)

LS “Don Milani”, Montichiari (BS)

LS Scienze Applicate “B. Russell”, Cles (TN)

LS “Visitandine-Malpighi”, Castel San Pietro Terme (BO)

LS “Aristosseno”, Taranto

Ist. Comp. “G. Deledda”, Ginosa (TA)

Ist. Comp. “G. Deledda”, Pattada (SS)

 Come di consueto presentiamo tutti i commenti riuniti in questo unico file PDF (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

Il gruppo di lavoro che gestisce FLATlandia è composto da:

- Ercole CASTAGNOLA - NRD Università di Napoli “Federico II”
- Giuliano MAZZANTI - Docente di Geometria, Università di Ferrara
- Valter ROSELLI - Ricercatore, Dipartimento di Matematica, Università di Ferrara
- Luigi TOMASI - Insegnante di Matematica, LS "Galileo Galilei", Adria (RO)

| Home Page Cabri | Torna a FLATlandia | Archivi |