FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Ottobre 2008

Premessa

Prima di qualsiasi osservazione riguardante le soluzioni pervenute, i componenti del gruppo di Flatlandia vogliono riaffermare la loro disponibilità al proseguimento del lavoro dedicato a questa attività di sostegno e stimolo dell’insegnamento della geometria. Colgono l’occasione per ringraziare calorosamente tutti coloro che hanno voluto manifestare il loro sostegno al proseguimento dell’attività di “Flatlandia”.

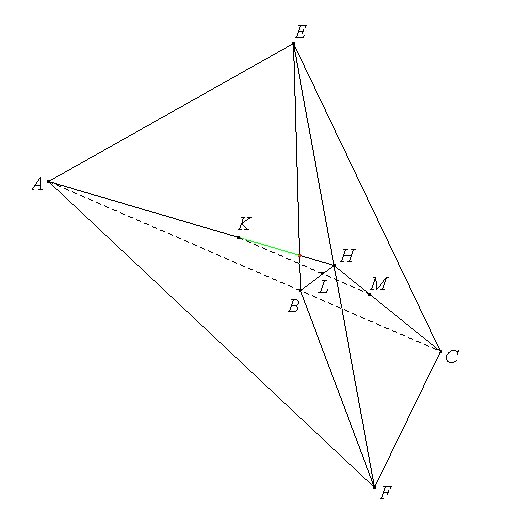
Sono dati, nel piano, tre punti distinti e allineati A, B, C. Siano, inoltre, E, F altri due punti distinti dello stesso piano e si considerino i triangoli AEF, BEF, CEF.

a) Indicati con K, L, M i baricentri dei tre triangoli, che proprietà hanno questi tre punti?

b) Se i triangoli AEF, BEF, CEF sono inoltre equivalenti, cosa si può dire delle rette AC ed EF ?

Dimostrare le proprietà individuate in a) e b). 

 

Commento


Sono giunte quattro risposte, due provenienti da Scuole Medie, una da una seconda Liceo Scientifico e una da una terza, sempre di Liceo.

Il problema richiedeva prima la proprietà comune di tre punti particolari (cioè, la verifica del loro allineamento) e poi, in una situazione particolare, la mutua posizione di due rette.

Alla prima domanda rispondono in modo sostanzialmente corretto (con alcune imprecisioni) gli studenti delle Scuole Superiori e di una Scuola Media, mentre tutti arrivano a risolvere il secondo quesito, con una puntualizzazione che ora segnaleremo. In particolare ci preme sottolineare quanto segue: a) si dovrebbero esaminare separatamente i due casi in cui i punti E, F si trovano dalla stessa parte rispetto alla retta a cui appartengono i punti A, B, C o da parti opposte [o, perlomeno, dire che la trattazione è analoga]; b) Cabri permette di congetturare una certa proprietà, ma non di dimostrarla; c) se due triangoli hanno la stessa area, questo non implica che le basi e le corrispondenti altezze abbiano la stessa lunghezza; d) se un punto K di un segmento AH divide il segmento in due parti tali che HK : KA = 1 : 2, allora AH = 3HK (intesa come relazione tra le relative lunghezze) e, quindi, l’omotetia di centro H che porta il punto A nel punto K ha rapporto 1/3 e non 1/2.

Sono pervenute risposte dalle seguenti scuole:

Si allega QUI il documento PDF con le risposte

NOTA: Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

| Home Page Cabri | Torna a FLATlandia | Archivi |