 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Novembre - Dicembre 2008
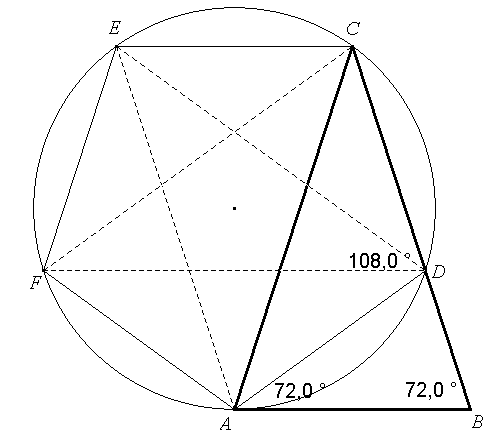
1) Utilizzando il goniometro o uno strumento informatico, disegnare un triangolo isoscele ABC i cui angoli alla base, di vertici A e B, misurino 72°.
2) Costruire la bisettrice dell'angolo di vertice A e indicare con D il punto in cui questa incontra il lato CB. Verificare che i segmenti AD e DC e l’angolo ÐADC sono rispettivamente due lati e un angolo di un poligono regolare. Di quale poligono si tratta?
3) Costruire i rimanenti vertici del poligono e tracciarne le diagonali. Quali considerazioni si possono fare su tali diagonali?
Descrivere le costruzioni richieste e motivare le risposte.
Commento
Sono giunte cinque risposte, due provenienti da due Scuole Medie, una da una seconda Liceo Scientifico e due da due classi terze, una di Liceo Scientifico e un’altra di un ITCG Programmatori.
Il problema richiedeva prima la costruzione di un particolare triangolo isoscele (cioè con gli angoli alla base di ampiezza pari a 72°), poi la costruzione di un particolare segmento (la bisettrice di un angolo), con la conseguente individuazione di un particolare poligono regolare (un pentagono). Infine il completamento del poligono regolare individuato e la costruzione delle sue diagonali, di cui si chiedeva di analizzare le relative proprietà.
Alla prima domanda rispondono correttamente solo gli studenti delle due classi terze [uno studente di terza media non fornisce indicazioni sulla costruzione, mentre gli studenti dell’altra terza media e la studentessa di seconda liceo iniziano direttamente dal secondo quesito]. Tutti rispondono in modo sostanzialmente corretto alla seconda e alla terza domanda [salvo alcune imprecisioni che segnaleremo caso per caso]. In ogni caso ci preme sottolineare quanto segue: a) le diagonali di un poligono vanno contate una sola volta e quindi le diagonali di un pentagono sono 5; b) i poligoni stellati hanno sempre un numero pari di lati [ogni “punta” della “stella” è costituita da 2 lati] e quindi non esiste il pentagono stellato [il poligono stellato a cui si fa riferimento è, in effetti, un decagono].
Sono pervenute risposte dalle seguenti scuole:
SM “C.A. Dalla Chiesa”, S.Genesio ed Uniti (PV)
SM “G.B. Tiepolo”, Milano (MI)
LS “Pitagora”, Rende (CS)
LS “Aristosseno”, Taranto (TA)
ITCG “Ruffini”, Imperia (IM)
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.
Si allega
QUI il documento
PDF con le risposte
| Home Page Cabri | Torna a FLATlandia | Archivi |