FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Dicembre 2007

IL TESTO DEL PROBLEMA

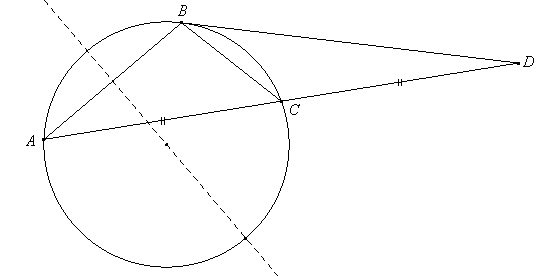
Data la corda AB di una circonferenza (diversa dal diametro), detto C un punto sull’arco maggiore AB, si prolunghi AC di un segmento CD congruente ad AC.

a) Che cosa si può dire dei triangoli ACB e CDB?

b) Determinare C in modo che il triangolo BCD abbia area massima.

c) Qualora sia verificata la proprietà di cui al punto b), stabilire la natura del triangolo ABD.

Motivare le risposte.

 


Commento

Abbiamo ricevuto dieci risposte così suddivise: due provenienti da Scuole Medie, tre dal biennio delle Scuole Superiori, quattro dal triennio delle Scuole Superiori (sempre III anno) e una da un Liceo in cui manca la precisazione dell’anno. Pensiamo che tutto questo sia una conferma del fatto che l’interesse per la geometria euclidea non è limitato al solo biennio delle Scuole Superiori.

Il problema poneva tre domande (tra loro collegate): nel primo quesito si chiedeva di individuare l’equiestensione di due triangoli; nel secondo di determinare in quale situazione l’area (comune) di tali triangoli risultava massima e nel terzo di individuare che, nella situazione corrispondente al secondo punto, il triangolo “somma” dei due era rettangolo.

In tutte le risposte pervenute viene risolto correttamente il primo quesito, mentre solo alcuni forniscono una dimostrazione esauriente di quale posizione deve assumere il punto C affinché l’area sia massima (altri forniscono una giustificazione dettata semplicemente dall’evidenza “visiva”). Infine per l’ultimo quesito alcuni mostrano di non aver ancora chiara la distinzione tra teorema diretto e teorema inverso: nel caso specifico il teorema diretto è “Se un triangolo è rettangolo, allora la mediana relativa all’ipotenusa è congruente alla metà dell’ipotenusa” [e questo è un teorema ben conosciuto], mentre il teorema inverso è “Se in un triangolo la mediana relativa a un lato è congruente alla metà di quel lato, allora il triangolo è rettangolo (e il lato in questione è l’ipotenusa)” e dovrebbe essere dimostrato.

Un’ultima preghiera: cercate di resistere alla tentazione di costruire figure gigantesche (questo non le rende più “leggibili”, ma solo più difficili da gestire). Per quanto riguarda la “leggibilità” è opportuno evitare di sovrapporre al piano euclideo il riferimento cartesiano.

Sono pervenute risposte dalle seguenti scuole:

 

Si allega QUI il documento PDF con le risposte
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre.

| Home Page Cabri | Torna a FLATlandia | Archivi |