Flatlandia - Aprile 2008

FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Disegnare su un cartoncino il triangolo rettangolo isoscele ABC, con l’ipotenusa AB che misura 10 (cm). Disegnare quindi il triangolo equilatero ABD col vertice D da parte opposta a C rispetto ad AB. Ritagliare la figura ottenuta e ripiegarla lungo il lato AB in modo che il vertice D venga a trovarsi sulla perpendicolare condotta per C al piano del triangolo ABC.

1) Considerare il tetraedro ABCD così ottenuto e determinare le lunghezze di tutti i suoi spigoli.

3) Dimostrare che le altezze del tetraedro concorrono in uno stesso punto; precisare la sua posizione.

4) Verificare che il quadrato dell’area del triangolo equilatero ABD è uguale alla somma dei quadrati delle aree degli altri tre triangoli che compongono il tetraedro ABCD.

Nota. Come ulteriore chiarimento del testo del problema, dedicato alla geometria solida, riteniamo opportuno inserire le tre figure seguenti elaborate dal prof. Luigi Tomasi, utilizzando il software Cabri 3D.

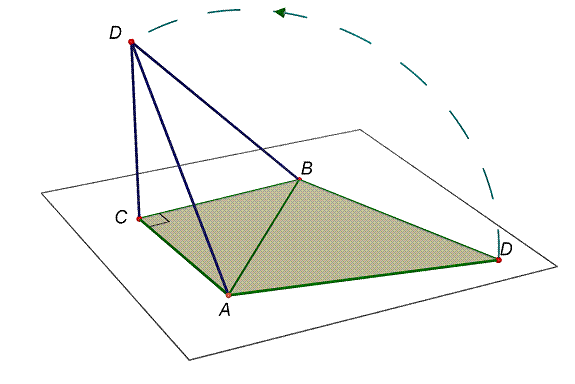
Figura 1

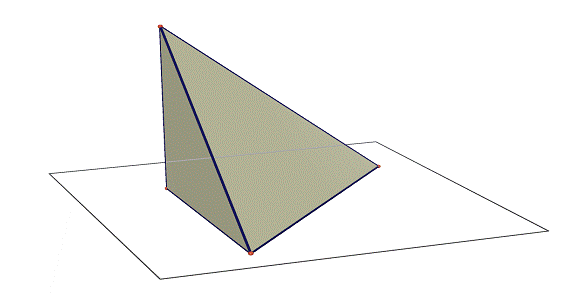
Figura 2

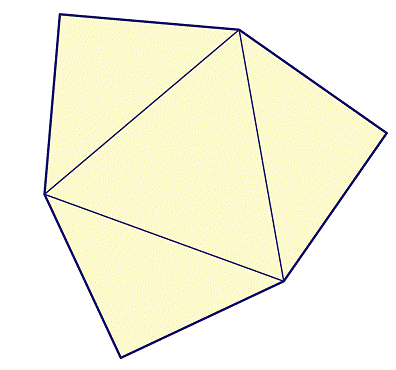
Figura 3

Commento

Abbiamo ricevuto tre risposte così suddivise: una da una Scuola Media, una dal biennio e una dal triennio di Scuole Superiori.
Il problema (oltre alle indicazioni per una costruzione “manuale” della figura solida) poneva quattro domande, di diversa difficoltà, tra loro direttamente o indirettamente collegate.
Al secondo quesito alcuni hanno risposto in modo corretto, fornendo però una giustificazione non del tutto completa.
A tale proposito ricordiamo che “una piramide si dice retta se nella sua base si può inscrivere una circonferenza il cui centro è il piede dell’altezza della piramide; in particolare se la base è un poligono regolare, la piramide si dice retta a base regolare (o comunemente piramide regolare)”.
Si osservi che un tetraedro può essere considerato come una piramide avente per base una qualunque delle sue facce, in tal caso i concetti precedenti si riferiscono ad una opportuna faccia considerata come base.
Anche al terzo quesito sono state fornite risposte non del tutto soddisfacenti.
Riteniamo peraltro apprezzabili tutte le risposte, anche in considerazione della “scarsa popolarità” della geometria solida nei diversi ordini scolastici.

Sono pervenute risposte dalle seguenti scuole:

SM “C.A. Dalla Chiesa”, S. Genesio ed Uniti (PV)
LS “Pitagora”, Rende (CS)
ITCG “Ruffini”, Imperia (IM)

Si allega QUI il documento PDF con le risposte

NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.