FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Marzo 2007

1) Sia u una arbitraria unità di misura di lunghezza. Ritagliare da un cartoncino un semicerchio di diametro 20u e con esso formare un cono. Quali caratteristiche presenta il cono ottenuto?

2) Si vuole tagliare il cono ottenuto in due solidi equivalenti con un piano parallelo alla base. Quale sarà la distanza del piano dal vertice del cono?

3) Siano A e B due punti che stanno sulla superficie laterale del cono. Qual è il cammino più breve per andare da A a B? Motivare la risposta.

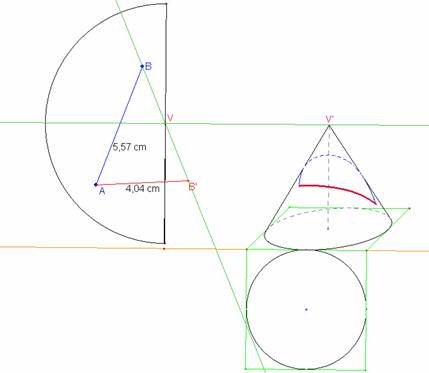Il percorso minimo si ottiene tracciando il segmento che congiunge i punti A e B oppure, in alternativa, i punti A e B’, essendo B’ il simmetrico del punto B rispetto al centro V del semicerchio che costituisce lo sviluppo laterale del cono.

Commento

Abbiamo ricevuto due risposte dalle scuole

• LS “Aristosseno”, Taranto (TA)
• SM “C.A. Dalla Chiesa” San Genesio ed Uniti, (PV)

Ci complimentiamo con gli studenti e gli insegnanti di queste classi per l’assiduo interesse che mostrano nei confronti della geometria euclidea, disciplina che viene spesso trascurata a favore delle tecniche di calcolo.

Nel problema si chiedeva di formare un cono da un semicerchio, di individuarne le caratteristiche, di dividerlo in due parti equivalenti con un piano parallelo alla base calcolando la distanza di quel piano dal vertice del cono.
Si chiedeva inoltre il minimo percorso per andare da un qualunque punto ad un altro sulla superficie laterale del cono.
In entrambe le risposte sono state risolte correttamente le prime due parti anche se con calcoli un po’ laboriosi, specialmente da parte degli studenti del liceo “Aristosseno”.
Si fa notare che due coni (o piramidi o prismi) simili hanno i volumi proporzionali ai cubi delle rispettive altezze. Questo consente di rispondere al secondo quesito in modo semplice e rapido.

Per quanto riguarda il terzo quesito, dobbiamo convenire che individuare quel percorso come tratto curvilineo sulla superficie del cono non è un quesito alla portata degli studenti di scuola secondaria.
Hanno pensato bene gli studenti della scuola media “Dalla Chiesa” a cercare la risposta considerando un opportuno sviluppo piano della superficie laterale del cono. Si vedano in proposito anche le nostre figure inserite nella loro risposta.

La figura allegata al testo illustra il terzo quesito nel caso analizzato (e non risolto) dagli studenti del liceo “Aristosseno”. Altre nostre figure sono inserite nella loro risposta

| Home Page Cabri | Torna a FLATlandia | Archivi |