 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Gennaio
2007
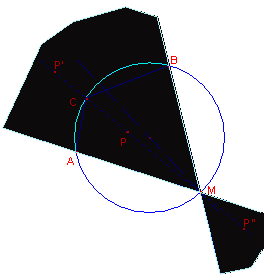
Sono dati un arco AB di
circonferenza e un punto P non appartenente ad essa. Individuare
sull’arco AB un punto C tale che la bisettrice dell’angolo ACB passi per
P.
La costruzione precedente è possibile per ogni scelta del punto P?
E’ facoltativo risolvere ora il seguente quesito: costruire un quadrato essendo dati un vertice e due punti appartenenti ai due lati (o ai loro prolungamenti) che non concorrono in quel vertice.
|
|
|
Commento
Sono giunte cinque risposte dalle scuole:
LS “Aristosseno”, Taranto (TA)
SM “C.A. Dalla Chiesa”, San Genesio ed Uniti (PV)
LS “G.B. Scorza”, Cosenza (CS)
LST, ITI “Berenini”, Fidenza (PR)
LS “Teresa Gullace”, Roma (RM)
Nel problema proposto si richiedevano due costruzioni, la prima delle quali forniva un metodo per risolvere la seconda.
Primo quesito.
Si trattava di costruire, scelto un arco di circonferenza, l’angolo in esso
inscritto la cui bisettrice passasse per un punto P prefissato, non
appartenente alla circonferenza. Si chiedeva inoltre di indagare sulla
possibilità di ottenere il risultato richiesto.
Nelle risposte ricevute è stata individuata solo parzialmente la regione di
piano in cui considerare i punti P che consentono di eseguire la
costruzione.
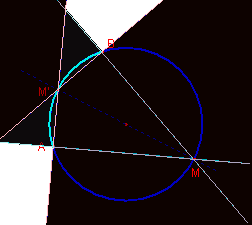
Gli studenti del LS “Aristosseno” non hanno fissato un solo arco, ma
considerato la possibilità di utilizzare l’uno o l’altro dei due archi che
vengono a formarsi, giungendo poi alla errata conclusione che il problema
abbia una soluzione dovunque si prenda il punto P. Si veda in proposito la
seconda figura che illustra il problema.
Secondo quesito.
Si chiedeva di costruire un quadrato dati un vertice e due punti
appartenenti ai due lati (o ai loro prolungamenti) che non concorro in quel
vertice. In tal modo diventa possibile ottenere la soluzione utilizzando la
costruzione precedente, nel caso particolare che l’arco sia una
semicirconferenza, qualunque sia la posizione dei tre punti.
Gli studenti della SM “C.A. Dalla Chiesa” non hanno raccolto tale
suggerimento, ma hanno fornito una costruzione basata sulle proprietà della
rotazione attorno a un punto, dedotta da osservazioni sulla figura
risultante.
Abbiamo stabilito di presentare le seguenti risposte:
LS “Teresa Gullace”: alcuni studenti della classe 2F hanno risolto entrambi i quesiti e motivato le costruzioni. Sono stati un po’ imprecisi nelle conclusioni.
SM “C.A. Dalla Chiesa”: la risposta del gruppo di studenti della classe 3S presenta qualche carenza nelle motivazioni, giustificabile, come più volte detto, per una scuola media inferiore.
Si allega QUI il documento PDF completo. Commenti ed eventuali correzioni, sono in parentesi quadra nelle risposte. Con doppia parentesi quadra sono indicate le parti omesse perché ritenute superflue.
| Home Page Cabri | Torna a FLATlandia | Archivi |