 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Febbraio
2007
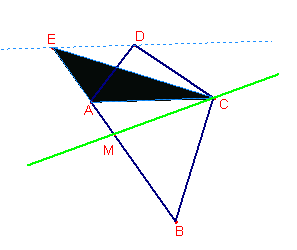
Per dividere in due parti equivalenti la superficie di un triangolo mediante una retta passante per un vertice è sufficiente congiungere quel vertice con un opportuno punto del lato opposto. Quale?
E’ possibile dividere un quadrilatero in due parti equivalenti con una retta passante per un vertice? Come?
Motivare le risposte.
 |
 |
|
|
S(MCE) = S(MCDA) = S(MBC) |
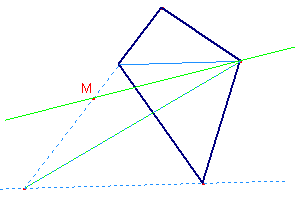
Se il punto M non è su un
lato del quadrilatero, |
Commento Febbraio
Abbiamo ricevuto cinque risposte, una da una scuola che finora non aveva partecipato, alla quale diamo il benvenuto, e una priva dei dati richiesti per essere inserita nell’elenco.
LS “Aristosseno”, Taranto (TA)
LST,ITI “Berenini”, Fidenza (PR)
LS “G.C. Vanini”, Casarano (LE)
SM “G.B.Tiepolo”, Milano (MI)
Nel problema di questo mese si chiedeva di dividere un quadrilatero in due parti equivalenti mediante una retta passante per un suo vertice, dopo aver ricordato come si riesce ad ottenere lo stesso risulato in un triangolo.
Si precisa che per quadrilatero, senza altri attributi, si deve intendere un generico quadrilatero convesso.
Si ribadisce inoltre che le costruzioni geometriche debbono essere eseguibili con riga e compasso anche quando si fa ricorso allo strumento informatico, quindi non ammettono il trasporto di misure derivate da calcoli aritmetici.
Le risposte ai problemi di FLATlandia riservano spesso delle sorprese: avevamo pensato che il primo quesito avrebbe indirizzato gli studenti a trasformare il generico quadrilatero in un triangolo, come mostra la nostra costruzione allegata al testo, per cercare poi la risposta al problema individuando il vertice più opportuno per il quale far passare la retta richiesta. Non sempre è andata così nelle risoluzioni ricevute.
Esaminiamo brevemente quelle che presenteremo:
Parrotta Lorenzo, LS “G.C. Vanini”, dopo aver risolto con prontezza il primo quesito, non ha utilizzato subito la trasformazione suddetta nel quadrilatero, ha seguito un percorso meno immediato che ha portato alla risoluzione senza incontrare la difficoltà della scelta del vertice più idoneo.
LST “Berenini”, Nicola Eslava e Gabriele Artusi hanno risolto la prima parte ricorrendo a un ragionamento laborioso e non completamente giustificato. Nella seconda, hanno trasformato subito il quadrilatero in un triangolo individuando la retta cercata, senza chiedersi se la soluzione sia possibile per ogni scelta del vertice. Presenteremo la seconda parte.
LS “Aristosseno”, gli studenti della classe 2M hanno considerato, nella seconda parte, solo quadrilateri particolari, trovando per i trapezi una interessante costruzione. Proporremo questa parte della loro risposta.
Ci dispiace di non poter presentare alcuna risposta delle scuole medie inferiori, in quanto abbiamo riscontrato in esse varie imprecisioni di procedimento.
Si allega QUI il documento PDF completo. Commenti ed eventuali correzioni, sono in parentesi quadra nelle risposte. Con doppia parentesi quadra sono indicate le parti omesse perché ritenute superflue.
| Home Page Cabri | Torna a FLATlandia | Archivi |