 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Gennaio 2004
Il testo del problema:
In un triangolo rettangolo scaleno ABC, di ipotenusa BC, siano I, K, J i punti medi di ciascun lato.
a) Costruire la circonferenza circoscritta al triangolo IKJ e verificare che essa passa per cinque punti che appartengono ai lati del triangolo ABC. Caratterizzare quelli diversi da I, J, K.
b) Se il triangolo è scaleno, ma non rettangolo quanti sono, in generale, i punti di intersezione dei suoi lati con la circonferenza? Caratterizzare quelli diversi da I, J, K.
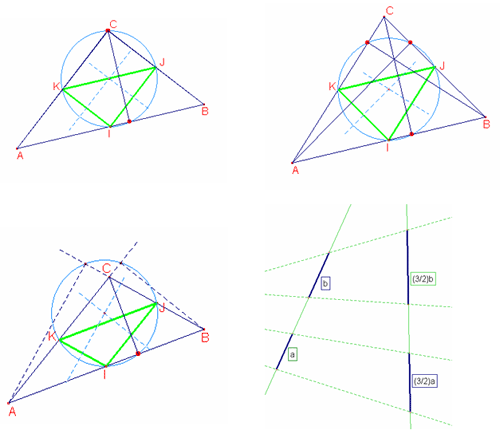
COMMENTO
Sono giunte in tutto undici risposte provenienti da cinque scuole secondarie superiori e da quattro scuole medie inferiori:
Nel problema proposto si chiedeva di determinare le
ulteriori intersezioni, con i lati di un triangolo, della circonferenza passante
per i punti medi dei lati del triangolo dato. Si proponeva prima il caso
particolare del triangolo rettangolo con lo scopo di facilitare poi la risposta
per il caso generale di un qualunque triangolo scaleno.
Nella risoluzione dei quesiti proposti si poteva utilizzare una “nota” proprietà
dei triangoli che afferma: “il segmento che congiunge i punti medi di due lati
…” (vedi risposta del LS “Farinato”) oppure dedurre la stessa dal Teorema di
Talete nella sua formulazione più generale, applicato però direttamente (vedi
risposta di Giacomo Canevari, LS “Aselli”, seconda parte).
Poiché gli studenti cambiano, ripetiamo ancora
(vedi FLATlandia Marzo 2001) che
NON ESISTE in generale L’INVERSO del teorema di Talete come si può dedurre
dalla figura che alleghiamo a questo commento.
Alcune delle risposte pervenute non sono accettabili o per incompletezza o per
assenza di motivazioni; in altre invece si riscontra una eccessiva complessità
nelle giustificazioni.
Le risposte ritenute valide, anche se presentano qualche imprecisione di esposizione e/o di procedimento, offrono una esauriente risoluzione del problema; in esse infatti si considerano entrambe le situazioni che possono presentarsi nella generalizzazione proposta nella seconda parte.
Abbiamo scelto le seguenti soluzioni:
Soluzione proposta da:
Classe 3° B - Scuola Media di Venasca (CN)
Punto A) Costruita la figura assegnata, [per una maggior completezza si doveva precisare come si costruisce la circonferenza] il triangolo IKJ risulta simile al triangolo ABC (figura 1)
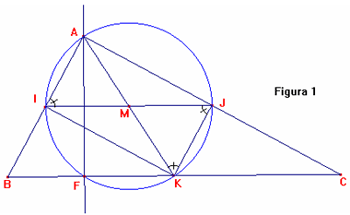
(applicazione inversa del teorema di Talete: se due rette
trasversali individuano su di un fascio di rette segmenti proporzionali, allora
il fascio di rette è formato da rette parallele) [Affermazione NON CORRETTA -
vedi commento – anche se in questo caso la retta per i punti medi è parallela al
lato] e congruente agli altri tre triangoli individuati AIJ, BIK e JKC. Pertanto
poiché il triangolo IAJ è un triangolo rettangolo con l’ipotenusa coincidente
con il diametro della circonferenza, il punto A appartiene alla circonferenza ed
è il primo dei punti richiesti. In conseguenza di quanto sopra, il quadrilatero
AIKJ risulta essere un rettangolo e la sua diagonale AK coincide anch’essa con
il diametro della circonferenza, per cui, disegnata la retta AF (essendo F il
quinto punto d’intersezione della circonferenza con il triangolo ABC), l’angolo
AFK è anch’esso un angolo retto, per cui l’ ulteriore punto d’intersezione della
circonferenza con il triangolo ABC risulta essere il piede dell’altezza del
triangolo assegnato.
Questo vale anche nel caso di triangoli scaleni qualsiasi (punto B)
(figura 2); se il triangolo è acutangolo si hanno altri tre punti d’intersezione
(D, E, F), mentre se è ottusangolo si ha solo un quarto punto, dato che in
questo caso solo un’altezza risulta interna al triangolo.
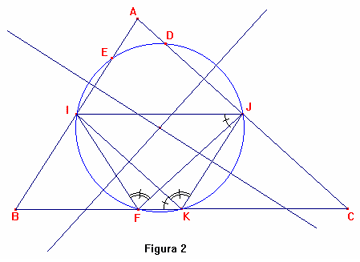
Preso ad esempio di nuovo il punto F [intersezione della
circonferenza col] lato BC , il triangolo IFJ risulta anch’esso congruente ai
quattro triangoli AIJ, IBK, IKJ e JKC perché ha il lato IJ in comune con i
triangoli AIJ e IKJ ed ha i due angoli IFJ ed IJF congruenti rispettivamente con
gli angoli IKJ e IKB (congruente sia a KIJ ed a IJA) perché angoli alla
circonferenza che insistono sullo stesso arco (AJ per i primi due angoli, IF per
i secondi).
Di conseguenza il triangolo IFJ risulta essere il simmetrico del triangolo AIJ
con asse di simmetria il lato IJ ; l’altezza condotta da A sulla base IJ avrà lo
stesso piede dell’altezza del triangolo IFJ condotta da F [essendo A ed F
simmetrici] e pertanto F risulta essere il piede dell’altezza relativa al lato
BC del triangolo ABC, come volevasi dimostrare.
Discorso identico si può fare per gli altri due punti D ed E, e risulta anche
dimostrato che se il triangolo è rettangolo due punti coincideranno con il
vertice dell’angolo retto, mentre se il triangolo è ottusangolo si ha solo un
quarto punto.
Soluzione proposta da:
Classe I C, Liceo Scientifico “P. Farinato” - Enna (EN)
Premesse:
Caso a)
Siano I e K i punti medi dei cateti AB e AC. La circonferenza richiesta passante
per I, J e K passerà anche per A perché l’angolo IAK è retto, [l’affermazione è
valida se prima si fa notare che, essendo IJ perpendicolare a JK, la
circonferenza ha diametro IK] passerà per un quarto punto Y ed avrà come
diametro IK [vedi precedente nota].
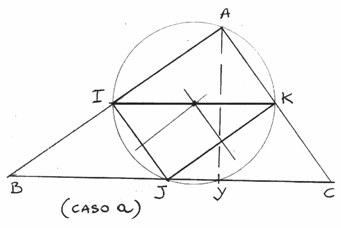
La corda JY appartiene all’ipotenusa BC, parallela al diametro IK e individua il trapezio IKYJ isoscele (vedi dimostrazione “Trapezio Isoscele”).
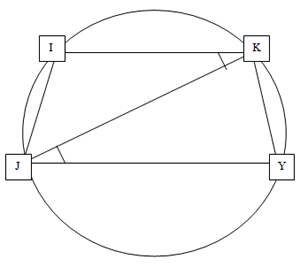
Dimostrazione “Trapezio Isoscele”
Date le due corde parallele IK e JY consideriamo la diagonale JK; gli angoli IKJ
e YJK sono congruenti perché alterni interni di due parallele tagliate da una
trasversale, di conseguenza sono congruenti gli archi IJ e KY che essi staccano
sulla circonferenza e le corde IJ e KY che sono i lati obliqui del trapezio
IKYJ.
Segue che KY = IJ = KC = KA, quindi il triangolo ACY, avendo la mediana YK = 1/2 AC, è rettangolo ( vedi dimostrazione “Triangolo Rettangolo”) e il quinto punto Y è il piede della perpendicolare condotta da A all’ipotenusa BC.
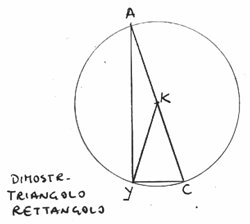
Dimostrazione “Triangolo Rettangolo”
I punti A, Y e C sono equidistanti dal punto K, esisterà quindi una
circonferenza di centro K e raggio la distanza comune passante per A, Y e C; ma
i punti A,K e C appartengono alla stessa retta e la distanza AC è il doppio del
raggio, per cui AC è un diametro. L’angolo AYC che insiste sul diametro AC è
retto; il triangolo AYC è rettangolo.
Notiamo che il punto A è allo stesso tempo il piede della perpendicolare condotta da C ad AB e il piede della perpendicolare condotta da B ad AC.
Caso b)
Non esiste un caso generale, ma due casi.
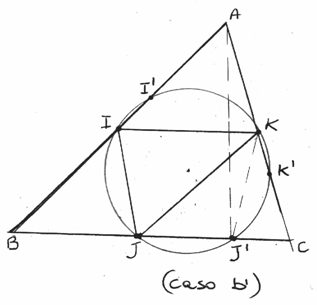
b1) Se il triangolo ABC è scaleno-acutangolo, i tre vertici A,B e C risultano tutti esterni alla circonferenza e ripetendo il ragionamento del caso a) si ottiene che ciascuno dei tre lati risulta intersecato dalla circonferenza in due punti di cui uno è il suo punto medio e l’altro il piede dell’altezza condotta ad esso dal vertice opposto. Totale sei punti di intersezione.
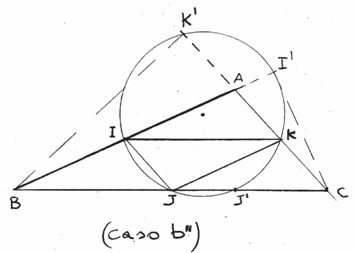
b2) Se il triangolo è scaleno-ottusangolo, sia A il
vertice dell’angolo ottuso. In questo caso il punto A risulta interno alla
circonferenza. Il lato BC è intersecato dalla circonferenza in due punti di cui
uno è il suo punto medio e l’altro il piede dell’altezza condotta ad esso dal
vertice opposto, mentre i lati AB e AC sono intersecati solo nel punto medio.
Totale quattro punti di intersezione.
Considerando però i prolungamenti dei lati AB e AC, questi vengono ulteriormente
intersecati dalla circonferenza in due punti ciascuno dei quali è il piede
dell’altezza relativa a ciascun lato.
Soluzione proposta da:
Giacomo Canevari - Classe 2° C
Liceo scientifico “G. Aselli” - Cremona (CR)
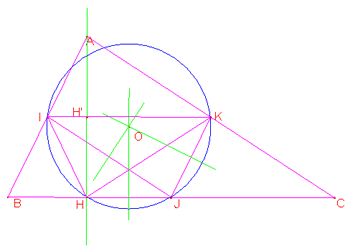
La costruzione si basa sul principio che, dato un triangolo, quello determinato dai punti medi dei tre lati è ad esso simile. Sappiamo infatti che il triangolo ABC e AIK sono simili, perché hanno un angolo (BAC) in comune e due lati rispettivamente proporzionali (AB e AI, AC e AK). Dunque l’angolo AIK è congruente a ABC, e poiché sono angoli corrispondenti, IK è parallelo a BC. La stessa dimostrazione si può ripetere per gli altri lati; da ciò, [[…]], si deduce che i due triangoli ABC e IJK sono simili, che ogni lato del primo è il doppio del corrispondente, e che i triangoli AIK e IJK sono congruenti.
Dimostriamo che, se O è il circocentro del
triangolo IJK e H il piede dell’altezza relativa a BC, allora OH = OJ. Per prima
cosa, notiamo che AH = HH', dove H' è l’intersezione tra AH e IK: per il teorema
di Talete, AB/AI = AH/AH', ma essendo AB = 2 AI, [segue che] AH = 2 AH'. Allora
i due triangoli AH'I e HH'I sono congruenti per il [primo] criterio: H'I è in
comune, AH = HH', gli angoli AH'I e HH'I sono congruenti perché retti.
Se ne ricava che IH = AI = KJ; ma, poiché IK // BC, anche le proiezioni di IH e
di KJ su KI devono essere congruenti. Si deduce che, per differenza di segmenti
congruenti, l’asse del segmento IK coincide con quello di HJ e, appartenendo O
al primo, deve appartenere anche al secondo. È dunque dimostrata la proprietà
precedente; H appartiene alla circonferenza circoscritta ad IJK.
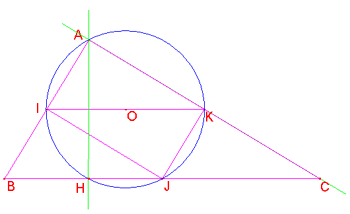
a. I punti di intersezione tra il triangolo ABC e la circonferenza circoscritta ad IJK sono, per la proprietà sopra dimostrata, i piedi delle altezze. Se ABC è rettangolo scaleno, essi sono H, piede dell’altezza relativa all’ipotenusa, e A, piede delle altezze relative ai cateti, che coincidono con i cateti stessi.
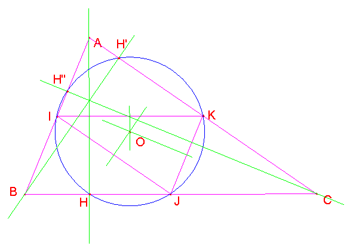
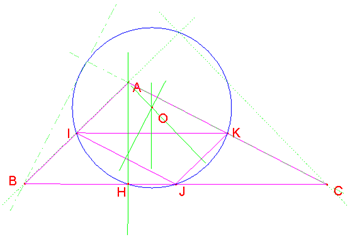
b. Se ABC è scaleno acutangolo, i punti di intersezione con la circonferenza sono tre, i tre piedi delle perpendicolari: H, H' e H''. Ma se ABC è scaleno ottusangolo, il punto è uno solo: infatti le altre due altezze sono esterne al triangolo.
| Home Page Cabri | Torna a FLATlandia | Archivi |