FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Marzo 2001

Il testo del problema:

E' dato un trapezio isoscele ABCD, con base maggiore AB. Siano a, b, c, d le bisettrici degli angoli interni del trapezio, rispettivamente di vertice A, B, C, D. Indichiamo con P, Q, R, S i punti di intersezione, supposti distinti, rispettivamente di a con b, b con c, c con d, d con a.

1) Quali proprietà ha il quadrilatero PQRS? E' inscrivibile? E' circoscrivibile? Come sono le sue diagonali rispetto alle basi del trapezio?

2) Se il trapezio ABCD non è isoscele, indicate alcune caratteristiche, fra quelle del precedente punto 1), che ancora si conservano.

Motivare le risposte.

Figure realizzate dalle Classi quinte, Scuola elementare "G. Galilei" di Alessandria:

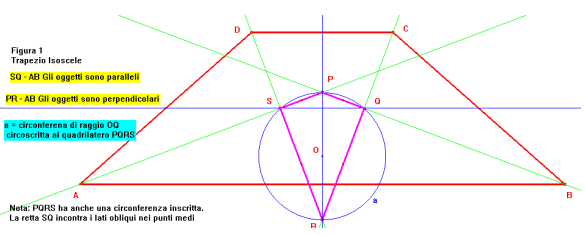
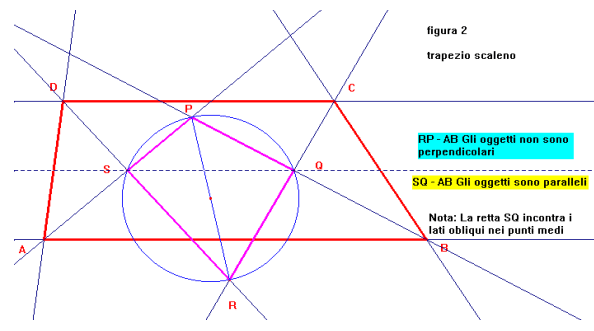
Commento

Abbiamo ricevuto undici risposte provenienti da dieci scuole, tre delle quali sono Scuole medie inferiori, e una risposta senza indicazioni sulla classe e sul tipo di scuola. Ci sono pervenute inoltre le figure inviate da una quinta classe della Scuola elementare "Galilei" di Alessandria, che avevamo già avuto il piacere di annoverare fra le scuole partecipanti alla attività. Utilizzeremo queste figure a corredo di questo commento

Il problema di Marzo richiedeva di individuare e giustificare le varie proprietà di un quadrilatero formato dalle bisettrici degli angoli interni di un trapezio isoscele; di analizzare poi, passando al caso generale del trapezio scaleno, quali erano invarianti.
La proprietà più notevole da dimostrare, che nel testo del problema non abbiamo volutamente richiesto in modo esplicito, è che una delle diagonali del quadriletero appartiene ad una retta parallela alle basi e passante per i punti medi dei lati obliqui, qualunque sia il trapezio.

Nelle risposte che abbiamo ricevuto il problema è stato affrontato in due modi.
Chi nella prima parte ha fatto ricorso alla simmetria (scuole medie e liceo di Bitonto), non ha avuto difficoltà a dimostrare il parallelismo ma non ha rilevato la proprietà dei punti medi.
Chi invece ha utilizzato nella dimostrazione delle varie proprietà la congruenza dei triangoli, non sempre e' riuscito a dimostrare in modo corretto il parallelismo; qualcuno ha individuato il passaggio per i punti medi, ma solo in due risposte e' stato giustificato.

Ci sembra utile soffermarci su questi ultimi fatti, con alcune considerazioni.
Nella prima parte, è semplice dimostrare il parallelismo considerando, per esempio, una opportuna coppia di triangoli isosceli con l'angolo al vertice in comune e, solo dopo, si può invocare il teorema di Talete per giustificare il passaggio della parallela alle basi per i punti medi dei lati obliqui.

Nella seconda parte la situazione è più delicata. Si può procedere nel seguente modo (valido anche per la prima parte): si costruisce prima una retta parallela alle basi passante per S (un estremo della diagonale del quadrilatero), quindi si ricorre al teorema di Talete e alla unicità del quarto proporzionale per affermare che tale parallela passa per Q (l'altro estremo).

Ricordiamo inoltre che, in generale, NON ESISTE il TEOREMA INVERSO di Talete. Solo nel caso del triangolo c'è un teorema che afferma che se una retta divide due lati in parti proporzionali, allora e' parallela al terzo lato (e si dimostra come abbiamo indicato sopra).
Si veda in proposito la soluzione del LS "Amaldi" di cui riporteremo la prima parte corredata da una nostra nota.

In qualche risposta è stato analizzato anche il caso del trapezio rettangolo, ma questo rientra in quello generale del trapezio scaleno. In una sola risposta, quella della SM di Rufina, è stata considerata la situazione particolare in cui il quadrilatero degenera; riportiamo le testuali parole: "Se le bisettrici a e d si incontrano sull'asse r [asse di simmetria del trapezio isoscele] il poligono PQRS si riduce ad un punto [centro della circonferenza inscritta nel trapezio]"

Fra le risposte pervenute tre non sono accettabili perché, pur provenendo da scuole superiori, in esse ci si limita ad osservare le proprietà delle figure costruite senza fornire giustificazioni.
Una sola risposta è completa, quella inviata dal LS "F. d'Assisi", che non riporteremo integralmente perché presenta inutili ripetizioni.
Le rimanenti, come già detto, o sono corrette, ma incomplete, oppure contengono errori nelle giustificazioni. Presenteremo di alcune le parti più apprezzabili.

Le scuole che hanno partecipato sono:

• Scuola Elementare "G. Galilei", Alessandria (AL)
• Scuola Media di Roveredo in Piano (PN)
• Scuola Media di Rufina (FI)
• Scuola Media di S. Genesio (PV)
• LS "Michelangelo", Forte dei Marmi (LU)
• LS "E. Amaldi", Bitetto (BA)
• LS "G. Galilei", Bitonto (BA)
• LS "F. D'Assisi" Roma (RM)
• LS "G. Ferraris" Torino (TO)
• ITG "Rondani" Parma (PR) (due risposte)
• ITI, LST "Berenini" Fidenza (PR)
• Farina e Nodari (Scuola?, Classe?)

Presentiamo di seguito le soluzioni delle seguenti scuole:

• Classe 3P di S. Genesio, simile nel metodo a quelle della SM di Rufina e della Scuola Media di Roveredo, ma più concisa della prima nella esposizione e più completa nelle della seconda motivazioni.
• Come già detto nel commento, LS "F. D'Assisi" (una soluzione simile ha inviato anche il LS "Michelangelo", che enuncia ma non giustifica il passaggio della parallela alle basi per i punti medi) e LS "E. Amaldi"
• LS "G. Galilei" di Bitonto, la prima parte in quanto si differenzia dalle precedenti nel metodo di dimostrazione.

NOTA: Le correzioni al testo o i commenti sono scritti in parentesi quadra. Sono racchiuse in doppia parentesi quadra le parti ritenute superflue.

Soluzione proposta da:
Classe 3P Scuola Media di San Genesio (Pavia)

1- Il trapezio isoscele ABCD è dotato di un asse di simmetria [retta "t" passante per i punti medi delle basi]. Le bisettrici "a" e "b", di due angoli corrispondenti (DAB e ABC), sono rette corrispondenti nella simmetria di asse "t", quindi il punto d'intersezione delle bisettrici (P) non può che essere un punto fisso appartenente all'asse "t".
Anche le bisettrici "d" e "c" si corrispondono nella stessa simmetria di asse "t", e quindi il punto R d'intersezione sarà sull'asse "t". I punti S [intersezione di "a" con "d"], Q [intersezione di "b"con "c"] sono punti corrispondenti nella simmetria di asse "t" perché intersezioni di rette corrispondenti.
Per questo motivo il segmento SQ è perpendicolare all'asse e i punti S, Q sono equidistanti dall'asse.
Perciò il quadrilatero PQRS è un deltoide .

2- Poiché nel trapezio isoscele gli angoli BAD+ADC=180° e le rette "a" e "d" sono bisettrici di questi angoli, gli angoli SAD+ADS=90°.
Per cui DSA è un angolo retto e anche PSR, essendo l'angolo opposto al vertice, è anch'esso retto.
Per lo stesso motivo è retto anche l'angolo PQR, quindi il quadrilatero PQRS è inscrittibile in una circonferenza per il teorema: un quadrilatero è inscrittibile se [[la somma de]]gli angoli opposti [[è]] sono supplementari.
Poiché abbiamo dimostrato che il quadrilatero è un deltoide, allora è circoscrittibile ad una circonferenza per il teorema: un quadrilatero è circoscittibile ad una circonferenza se la somma dei [di due] lati opposti è uguale [alla somma degli altri due].

3- Le diagonali del quadrilatero sono: la minore, SQ, è parallela alle basi; la maggiore, PR, è perpendicolari alle basi.

4- Se il trapezio ABCD non è isoscele abbiamo notato che si conserva l'inscrittibilità della figura ottenuta dall'intersezione delle bisettrici.Questo avviene perché gli angoli, anche in un trapezio scaleno, adiacenti ad un lato sono supplementari.Inoltre la diagonale minore rimane parallela alle basi (verifica con Cabri)

Soluzione proposta da:
Stefano Politi  e  Emiliano Langella - Classe 2B LS "F. D'Assisi" - Roma

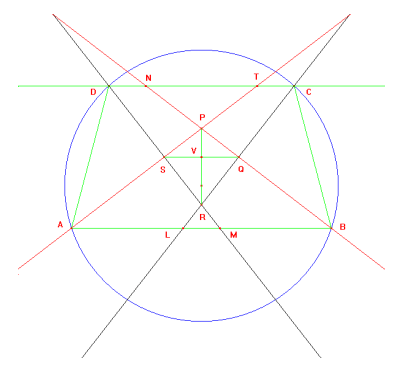
1)
Prendo in considerazione i triangoli

[I triangoli sono congruenti per il secondo criterio]
Quindi:
AS = BQ
DS = CQ
DSA = CQB = 90° perché A + D = 180° quindi ½ A + ½ D = 90° e la somma degli angoli interni di un triangolo è 180°.

Essendo PSR e PQR gli [angoli] opposti al vertice rispettivamente di DSA e CQB, misurano 90°.
Il quadrilatero PQRS è inscrivibile perché ha gli angoli opposti supplementari.

Prendo in considerazione i triangoli

[I triangoli sono congruenti per il secondo criterio]
Quindi:
AT = BN
DTA = BNC (angoli)
NC = DT

Il triangolo TNP come abbiamo dimostrato ha gli angoli alla base uguali, quindi è isoscele e TP = NP. Quindi risultano congruenti, per differenza di segmenti congruenti, PS e PQ.

Prendo in considerazione i triangoli
CLB e DMA
[[…]]
[In modo analogo si dimostra che] risultano congruenti, per differenza di segmenti congruenti; RQ e RS.

Quindi se PS = PQ e RQ = RS
PS + RQ = PQ +RS

Il quadrilatero PQRS è circoscrivibile perché la somma [[dei suoi]] di due lati opposti è uguale [alla somma degli altri due].

Prendo in considerazione i triangoli
PQR e PRS: RQ = RS per precedente dimostrazione
PQ = PS per precedente dimostrazione
PR in comune
[I triangoli sono congruenti per il terzo criterio]

Quindi QPR = SPR (angoli) e PRQ = PRS (angoli).
Quindi essendo PR bisettrice dell'angolo SPQ è anche bisettrice del suo opposto al vertice NPT (angolo). Essendo il triangolo NPT isoscele, la bisettrice relativa alla base coincide con l'altezza e con la mediana, quindi la diagonale PR è perpendicolare alle basi.

Prendo in considerazioni i triangoli
RVQ e RVS: RV in comune
SRV = QRV (angoli) per precedente dimostrazione
RQ = RS per precedente dimostrazione
[I due triangoli sono congruenti per il primo criterio]
Quindi QVR = RVS (angoli) e perciò sono retti, quindi le due diagonali sono perpendicolari. Quindi se una diagonale era perpendicolare alle basi l'altra sarà parallela.

CLB = DCL (angoli) perché alterni interni delle rette parallele DC e AB tagliate dalla trasversale CL ma essendo DCL = BCL (angoli) per ipotesi BCL = CLB (angoli), quindi CLB (triangolo) è isoscele. Essendo BQ la bisettrice relativa alla base del triangolo isoscele CBL, coincide con la mediana e con l'altezza, quindi CQ = QL. Con l'analogo discorso fatto questa volta sul triangolo DTA si dimostra che TS = SA.

Se conduciamo da Q la parallela alla base, incontrerà il lato CB nel suo punto medio perché come abbiamo dimostrato Q era punto medio di CL. Quindi la retta condotta da Q sarà sicuramente sul prolungamento di SQ perché altrimenti ci sarebbero due rette parallele alla base passanti per il punto Q.
[[…]]
[Si procede in modo analogo per il lato AD]

Quindi i prolungamenti di QS intersecano i lati uguali del trapezio isoscele nei loro punti medi.

2)

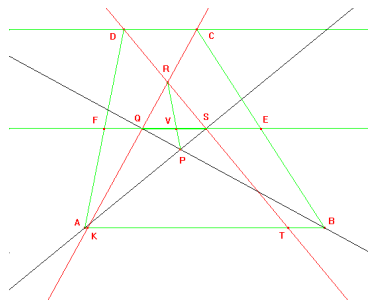
DCK = CKB (angoli) perché alterni interni delle rette parallele AB e CD tagliate dalla trasversale CK. Ma essendo BCK = DCK ( angoli ) per ipotesi risulta che KCB = CKB ( angoli ), quindi il triangolo BCK è isoscele con CB = KB.

[[…]] [Analogamente] il triangolo TDA è isoscele con AT = DA.

Nei triangoli isosceli le bisettrici dell'angolo al vertice coincidono con l'altezza e la mediana, quindi

CQ = QK.
CQB = BQK (angoli) = 90°
DS = ST
DSA = AST (angoli) = 90°

Se conduciamo la parallela alla base AB dal punto Q incontrerà il lato CB nel punto medio E perché Q era punto medio di CK.
[[…]] [Incontra anche DT in S e DA nel punto medio F]
Quindi SQ // AB // CD.

A + D = 180°, quindi nel triangolo DSA ½ D + ½ A = 90° e siccome la somma degli angoli interni di un triangolo è 180° DSA = 90°.

[Analogamente] CQB = 90°.

Quindi se il trapezio non fosse isoscele si conserverebbe il parallelismo di SQ rispetto alle basi, e il quadrilatero PQRS sarebbe sempre inscrivibile.

Soluzione proposta da:
Classe 2B Liceo Scientifico "E. Amaldi" - Bitetto (Bari)

1)
Il quadrilatero PQRS è convesso, ed ha queste proprietà:

- ha 2 angoli retti in S e in Q (gli angoli in A e in D sono coniugati interni supplementari, la somma delle loro metà ADS, SAD dà 90° e quindi per differenza ASD=PSR=90° e analogamente PQR=90°);

- ha coppie di lati consecutivi congruenti tra loro (AP=BP essendo il triangolo ABP isoscele per avere gli angoli alla base AB congruenti, perché metà degli angoli congruenti alla base maggiore del trapezio isoscele; AS=BQ essendo congruenti i 2 triangoli rettangoli ADS, BCQ per la congruenza dei lati obliqui AD,BC e degli angoli metà di quelli alle basi del trapezio isoscele: per differenza si ottiene PS=PQ e analogamente RS=RQ);

- ha diagonali perpendicolari (PS=PQ e RS=RQ comportano l'equidistanza di P ed R dagli estremi S e Q e quindi PR risulta asse della diagonale SQ);

- è inscrivibile per avere le somma degli angoli opposti supplementari (S=Q=90° =>S+Q=180° e per differenza anche P+R=180° essendo 360° la somma dei 4 angoli interni);

- è anche circoscrivibile per avere le somma dei lati opposti congruenti (PS+QR=PQ+SR essendo PS=PQ e RS=RQ);

- la diagonale SQ è parallela alle basi del trapezio (per il teorema di Talete RU/UD=RT/TC ma ADU facilmente isoscele sulla base DU con AS altezza-mediana comporta che DU=2*SU e analogamente BCT isoscele su CT comporta CT=2*QT; sostituendo si ottiene RU/(2*US)=RT/(2*TQ) da cui RU/US=RT/TQ che implica SQ parallela UT);

- quindi ha diagonali una perpendicolare e una parallela alle basi del trapezio.

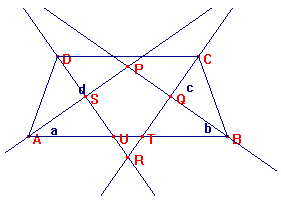
[NOTA: la dimostrazione del parallelismo di SQ è valida solo per la particolare figura in cui R è esterno al trapezio, per cui U e T si trovano sui lati dei triangoli DRC e SRQ. Se si modifica la figura in modo che R sia interno, per poter procedere nello stesso modo occorre mandare per R la parallela alle basi, applicare il teorema di Talete; poi condurre per S la parallela alle basi, applicare ancora il teorema di Talete, quindi, per la unicità del quarto proporzionale, concludere che Q appartiene a quest'ultima parallela. In questo modo la dimostrazione vale anche per il trapezio scaleno]

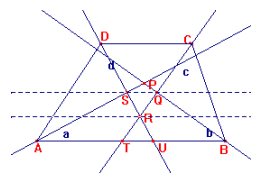
Soluzione proposta da:
Classe 2E - LS "G. Galilei" - Bitonto (BA)

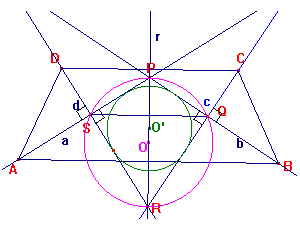
1]  Tracciato il trapezio isoscele e le bisettrici dei suoi angoli interni, facciamo le seguenti osservazioni:

• poiché il quadrilatero ABCD è un trapezio isoscele, gli angoli A e D sono supplementari tra loro e di conseguenza gli angoli ADS e DAS sono complementari in quanto metà di angoli supplementari quindi l'angolo DSA=90° quindi PSR=90° perché opposto al vertice. Analogamente per gli angoli in C e B, da cui CQB=90°, PQR=90°.
  Pertanto il quadrilatero SPQR è inscrittibile avendo una coppia di angoli opposti supplementari
  e in quanto entrambi retti, la circonferenza circoscritta ha l'ipotenusa comune PR come diametro.
• poiché il quadrilatero ABCD è un trapezio isoscele, ha la retta r, asse comune delle basi, quale asse di simmetria e quindi rispetto a tale retta si hanno le seguenti corrispondenze:
  (vertici) A -> B D -> C
  (angoli) A -> B D -> C
  (bisettrici) a -> b d -> c
  • Da cui segue che: il punto P rimane unito, essendo P= ab intersezione di rette corrispondenti;
    il punto R rimane unito, essendo R= cd intersezione di rette corrispondenti;
    quindi PR=r poiché per due punti passa una sola retta e l'asse di simmetria è
    l'unica retta luogo di punti uniti e pertanto PR perpendicolare alle basi del trapezio;
    al punto S= da corrisponde il punto Q= cb e quindi SQ, segmento congiungente
    punti corrispondenti, è perpendicolare all'asse r;
    quindi SQ // DC e ad AB;
• Il quadrilatero PQRS ha r come asse di simmetria;
• Al segmento SP corrisponde QP, al segmento SR corrisponde QR , quindi SP=QP e SR=QR in quanto la simmetria assiale è una isometria. Pertanto il quadrilatero PQRS è circoscrittibile alla circonferenza di diametro PR avendo la somma di due lati opposti congruente alla somma degli altri due: SP+RQ=PQ+SR.

[[…]]

| Home Page Cabri | Torna a FLATlandia | Archivi |