FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Settembre 2002

Commento

Nel commento alle risposte del problema di Febbraio vi proponemmo di dimostrare, entro il mese di Settembre, la seguente costruzione realizzata da un gruppo di ragazzi dell'ITI "Ferrari" di Torino, ma non giustificata. (vedi il commento al problema di Febbraio per i dettagli).

Costruzione proposta da
GUERNIERI MARCO, RANDO FRANCESCO, RODELLA ANDREA
Classe 2Ast - ITIS "E. Ferrari" Torino

Costruisco un quadrato di lato AB=a e traccio la sua diagonale; disegno una circonferenza di centro B con raggio AB che interseca la diagonale del quadrato ABCD in un punto O; traccio una circonferenza di centro O e raggio OA, che interseca il quadrato ABCD nei punti F e G; disegno la parallela a BC passante per F e la parallela ad AB passante per G che si incontrano nel punto E.
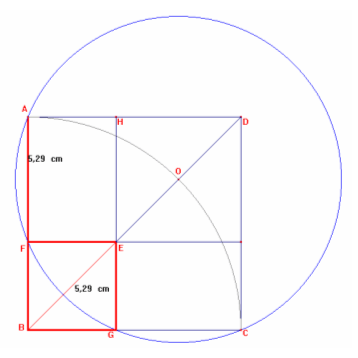PROPOSTA: dimostrare, senza ricorrere al calcolo algebrico, la seguente affermazione:  Il quadrato BFEG è quel quadrato in cui la somma del lato e della diagonale è uguale al segmento AB.

Abbiamo ricevuto tre risposte dalla scuola media "Leonardo da Vinci" di Rufina (FI). Ne presentiamo una, quella che abbiamo ritenuto più sintetica.

Riportiamo anche, in via eccezionale, la risposta inviata da Daniele Urzì, un ragazzo che, giunto ormai al quinto anno del liceo scientifico "G. Galilei" di Catania, ha continuato ad interessarsi ai problemi di FLATlandia.

Soluzione proposta da
Luisa Papi, Francesca Barasso, Helena Nocentini, Sara Vettori
S.M. “L. da Vinci”, Rufina (FI), classe 3B.

[Nella seguente dimostrazione sono indicati con a’ e d’ rispettivamente il lato e la diagonale del quadrato da costruire a partire dal segmento AB. NDR]

Consideriamo un qualsiasi quadrato ABCD: la proiezione [ortogonale] della diagonale AC sulla retta AB è congruente al lato del quadrato, la proiezione [ortogonale] del lato AB sulla retta BD è congruente a metà diagonale.
Per questo motivo il lato AB = (d’+ a’), riportato sulla diagonale BD, avrà come proiezione [ortogonale] BH = (a’+ 1/2 * d’)

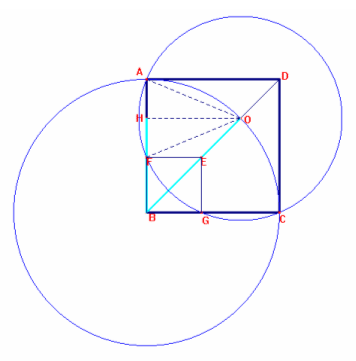
Quindi AH(AB – HB) = (a’+ d’) – (a’+ 1/2 * d’) = 1/2 * d’
L’uso del compasso, con centro in O e apertura OA, permette di individuare il punto simmetrico di A rispetto alla retta OH, asse di simmetria nel triangolo isoscele AOF.
Avremo così AF = d’, e di conseguenza FB = a’.

Soluzione proposta da
Daniele Urzì Liceo scientifico “G. Galilei”, Catania, classe 5B.

Siano t e v le circonferenze di centro rispettivamente B e O e raggio rispettivamente AB e OA.
In riferimento alla figura, il quadrilatero AFGC è inscritto in v, dunque la somma di due angoli opposti è un angolo piatto. Da ciò segue FGB=FAC=45°.
Discorso analogo per l’angolo BFG. Il triangolo FBG è quindi isoscele rettangolo (FB=BG). Rispetto a t si ha OCA=OBA/2=45°/2.
Il triangolo FOC è isoscele rettangolo, infatti, rispetto a v, è FOC=2*FAC=2*45°=90°.

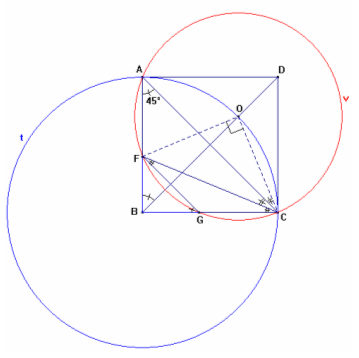
Poiché gli angoli OCF, OCA misurano rispettivamente 45° e 45°/2, anche ACF misura 45°/2.
Del resto l’angolo ACB misura 45° e quindi si ha FCG=45°/2.
Dovendo essere FCG+CFG=FGB=45°, segue CFG=45°/2; ciò significa che il triangolo FCG è isoscele su base FC.
Per le considerazioni fatte si ha FB+FG=BG+GC=AB, e si può concludere che il quadrato di lato FB è quello richiesto.

| Home Page Cabri | Torna a FLATlandia | Archivi |