FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Febbraio 2002

E' dato un segmento AB di lunghezza a.

1) Costruire un quadrato che abbia AB come somma tra la diagonale e il lato. Motivare la costruzione.

2) Calcolare in funzione di a il lato del quadrato ottenuto.

Commento

abbiamo ricevuto quattordici risposte provenienti da nove scuole, di cui cinque superiori e quattro inferiori.

Nel problema del mese di Febbraio si chiedeva di costruire un quadrato, a partire da un segmento assegnato che ne rappresentasse la somma del lato e della diagonale, e di calcolarne il lato in funzione della misura del segmento dato.

Eravamo perplessi sulla opportunità di proporre tale problema, ci ha invece sorpreso il numero delle risposte (che non si è discostato da quello che mediamente riceviamo) e la varietà delle soluzioni.
I ragazzi delle scuole superiori hanno in maggioranza privilegiato la soluzione algebrica e da questa dedotto la costruzione richiesta. Alcuni ragazzi dell'ITI Berenini hanno invece fornito una costruzione analizzando le proprietà della figura risultante.

Una bella costruzione, purtroppo senza giustificazione, ci è pervenuta dall'ITI Ferrari. Abbiamo pensato di presentarla alla fine di questo commento e di proporre la sua dimostrazione ai ragazzi che seguono questa attività, da inviare entro Settembre.

Altre tre risposte non sono state ritenute valide, una per incompletezza e due perché in esse non si è "costruito" il lato del quadrato geometricamente (con riga e compasso), ma "trasportata" la sua misura (approssimata) dalla calcolatrice del software Cabri. Questo non è un modo corretto per risolvere costruzioni geometriche.
Un elogio va ai ragazzi della scuola media inferiore che hanno proposto interessanti soluzioni, tre ricorrendo al Teorema di Talete o alla similitudine, e una basata sulla equivalenza.

Riporteremo una soluzione di ogni tipo, quella che riteniamo piu' esauriente, citando quelle analoghe.

Per la scuola superiore:

Per la scuola media inferiore riportiamo la prima parte di tre delle risposte pervenute (il calcolo del lato e' corretto, ma e' gia' presente in modo piu' completo nelle precedenti risposte):

Costruzione proposta da
GUERNIERI MARCO, RANDO FRANCESCO, RODELLA ANDREA
Classe 2Ast - ITIS "E. Ferrari" Torino

  • Costruisco un quadrato di lato AB=a e traccio la sua diagonale;
  • disegno una circonferenza di centro B con raggio AB che interseca la diagonale del quadrato ABCD in un punto O;
  • traccio una circonferenza di centro O e raggio OA, che interseca il quadrato ABCD nei punti F e G;
  • disegno la parallela a BC passante per F e la parallela ad AB passante per G che si incontrano nel punto E.

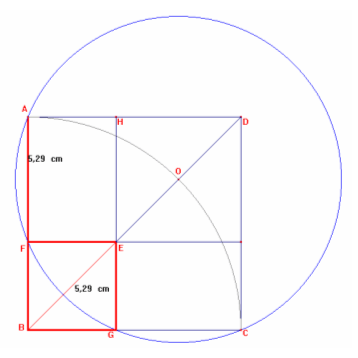PROPOSTA: dimostrare, senza ricorrere al calcolo algebrico, la seguente affermazione:  Il quadrato BFEG è quel quadrato in cui la somma del lato e della diagonale è uguale al segmento AB.

Soluzione proposta da:
Alessandro Studer 2°B s.t  - ITIS Berenini Fidenza (PR)

1) prendiamo prima in considerazione il quadrato CBED di lato l e diagonale CE = d.

- Riportiamo la diagonale d adiacente al lato CB.
- il segmento AB è uguale alla somma AC + CB ovvero d + l e quindi corrisponde al segmento proposto.

Congiungendo il punto A con il vertice E si individua il triangolo ACE che ha le seguenti caratteristiche:

- E’ isoscele perché ha due lati uguali (AC e CE) per costruzione.
- L’angolo ACE è di 90° + 45° = 135°.

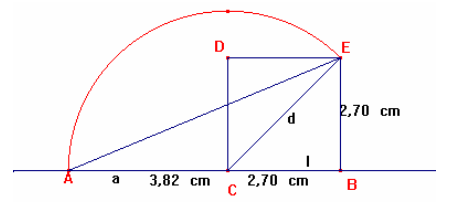
- Poiché isoscele gli angoli CAE e AEC sono uguali e valgono (180°-135°): 2 = 22,5° pari a ¼ di 90°.

Il problema sarà dunque risolto costruendo il triangolo ACE a partire dal segmento proposto AB.

- Tracciamo le perpendicolari al segmento AB per i punti A e B (p1 e p2).
- Tracciamo la bisettrice (b1) dell’angolo formato dalla retta p1 e dal segmento AB.
- Tracciamo la bisettrice (b2) dell’angolo formato dalla bisettrice b1 e da AB ed avremo due angoli di 22,5°.

L’intersezione tra b2 e p2 individua il punto E vertice del quadrato ed EB è un lato. E è un vertice del triangolo [isoscele].

- Tracciamo la parallela (p3) ad AB per E, individua il punto F su p1.
- L’angolo FEA è di 22,5° perché alterno interno con EAB.

- Tracciamo la bisettrice (b3) dell’angolo formato da p3 e p2, si individuano il punto C su AB e due angoli FEC e CEB entrambi di 45°.
L’angolo AEC è FEC - FEA = 45° - 22,5°.
L’angolo AEC è uguale a 180° - ECB = 180° - 45° = 135°. (ECB è alterno interno di FEC).

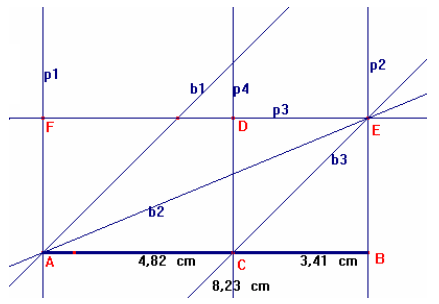
Il triangolo ACE è quello cercato; CB e BE sono due lati del quadrato che si completa con la perpendicolare ad AB per C (p4); l’intersezione con p3 individua il punto D.

Il segmento AC è uguale alla diagonale del quadrato ed AB è la somma di d+l.

2) Il lato del quadrato dato a si trova impostando l’equazione di primo grado: a = l + l*rad(2) da cui l = a / (1 + rad(2)) e razionalizzando l = a*(rad(2) - 1).

Soluzione proposta da:
Santini Mattia 2° st ITI “Berenini” Fidenza PR

1) Si inizia disegnando il quadrato ABCD di lato AB. Sapendo che il lato AB è la somma del lato k e della diagonale d(uguale a k*sqr(2)) del quadrato da costruire si ha a uguale a k+k*sqr(2).
La lunghezza della diagonale AD è a*sqr(2) uguale a k*sqr(2)+2k. Puntando il compasso in A con apertura AD si determina sulla semiretta AB il punto E. Ora sapendo che AE è uguale a k*sqr(2)+2k e che AB è uguale a k+k*sqr(2) sottraendo dal segmento AE il segmento AB si trova il segmento BE uguale a (k*sqr(2)+2k))-(k+k*sqr(2)) = k.
Con apertura BE puntando con il compasso nel punto A si determina il punto F sul segmento AB; in questo modo si trova il lato del quadrato AFGH.

 

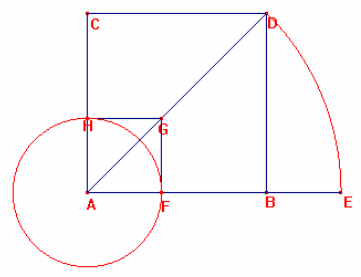
2) Per calcolare in funzione di a il lato del quadrato AFGH si imposta l'equazione a=k+k*sqr(2) si ottiene a=k*(1+sqr(2)) si calcola il valore di k=a/(1+sqr(2)) ora razionalizzando si ottiene che k=a*(sqr(2)-1).

Soluzione proposta da:
Scuola Media di Roveredo in Piano (PN)
Classe 2 A (Costruzione e motivazione 1a.)
Classe 3 A (Motivazione 1b, risposta 2. )

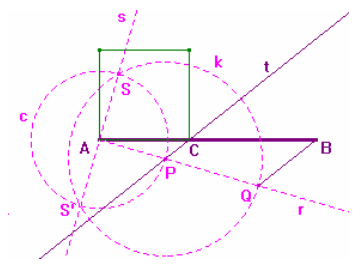
1. Dato il segmento AB.

Procedura:

1. Semiretta r di origine A;
2. Punto P su r;
3. Retta s perpendicolare ad r, passante per A;
4. Circonferenza c di centro A, per P;
5. Intersezione di c con s (S, S');
6. Circonferenza k di centro P, per S;
7. Intersezione di k con r (Q).

1.a)
- I segmenti AP e AS sono congruenti e perpendicolari per costruzione, quindi si possono considerare due lati consecutivi del quadrato di diagonale SP;
- Il segmento PQ è congruente con SP per costruzione;
- allora il segmento AQ è la somma del lato e della diagonale di un quadrato.

Procedura:

8. Segmento BQ;
9. Retta t parallela al segmento BQ [per P]; Intersezione di t con AB (C). Il segmento AC è lato del quadrato che ha per diagonale il segmento CB.

1b) - Triangoli APC e AQB sono simili avendo gli angoli corrispondenti congruenti per costruzione. Essendo i lati corrispondenti in proporzione lo sono anche le loro differenze, quindi: il rapporto tra AP e PQ è lo stesso del rapporto tra AC e CB.

Soluzione proposta da
Ilaria Andena e Sara Taha
classe IIIM - Scuola Media Statale “Bergamaschi” di Torrevecchia Pia (PV)

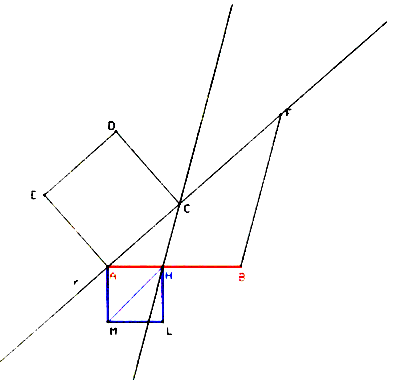
1°)  Sappiamo che, per il teorema di Pitagora, la diagonale di un quadrato di lato l misura .

Dobbiamo quindi dividere il segmento dato AB in due parti tali che il loro rapporto sia .

Procediamo così:

Disegniamo il segmento AB e una retta r passante per A e non per B. Prendiamo un qualunque punto C su di essa, costruiamo il quadrato di lato AC e chiamiamo F il punto di intersezione tra la retta r e la circonferenza di centro C e raggio CE. Poiché CF = EC (diagonale del quadrato) è CF:AC=. Uniamo F con B, tracciamo per C la parallela a BF e chiamiamo H il punto di intersezione di questa parallela con AB. Per il teorema di Talete CF:AC = HB:AH =

AH è il lato del quadrato richiesto.

Costruiamo il quadrato di lato AH

 

Soluzione proposta da
Sarti Elisa, Papi Luisa, Nocentini Helena, Barasso Francesca, Vettori Sara
classe 3B della scuola Media “L. da Vinci”, Rufina FI:
 

1.

Considero il quadrato ABCD ( costruito sul lato AB ) e stabilisco

AB = a;
AC = d (la sua diagonale);
AB’= a’ (il lato del quadrato richiesto);
AC’= d’ (la diagonale del quadrato medesimo);
a = a’ + d’.

Poiché tutti i quadrati sono simili avremo:

a : d = a’ : d’                         e, applicando il comporre
(a + d) : a = (a ’+ d’) : a’      e, sostituendo
(a + d) : a = a : a’
a^2= ( a +d) * a’

Quindi l’area del quadrato costruito su AB è equivalente all’area del rettangolo avente per base la somma del lato AB e della sua diagonale, l’altezza congruente al lato a’ richiesto.

Costruzione

1) Semiretta AB (origine A).
2) Quadrato ABCD.
3) Compasso, apertura AC centro in B.
4) Individuo il punto E di intersezione della circonferenza con la semiretta AB e costruisco il segmento AE.
5) Macro qua-rett-equiv. ( elementi di partenza: quadrato, semiretta AB, punto E ), per trasformare il quadrato ABCD nel rettangolo AEFD’ equivalente ad esso, di base AE. Chiamo D’ l’altezza di tale rettangolo sul lato AD.
6) Compasso apertura AD’, centro in A individuo il punto B’.
7) Quadrato AB’C’D’.
8) Compasso apertura AC’ centro in B’.

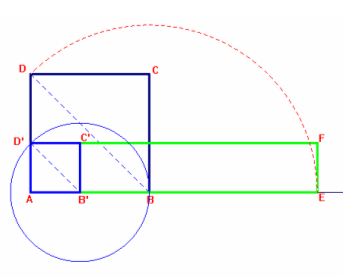
Osservo che la diagonale del quadrato è, come richiesto, congruente al segmento B’B.

 Per la Macro Qua-rett_equiv: 

1)          Semiretta AB, origine A.
2)          Considero il triangolo ABD, isoscele e rettangolo in A
3)          Segmento DE.
4)          Parallela a DE passante per B.
5)          Individuo il punto D’ intersezione di tale parallela con il lato AD.
6)          Triangolo AED’.

 Dimostriamo che il triangolo ABD è equivalente a AED’. Infatti :

 ABD =ABD’+ D’BD                e                 AED’ = ABD’+D’BE.

 Inoltre           D’BD =~ D’BE 

perché hanno stessa base D’B e stessa altezza ( la distanza tra le due rette parallele D’B e DE).

Quindi i due triangoli ABD e AED’ sono equivalenti perché equicomposti.

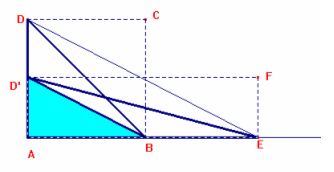
Di conseguenza anche il quadrato ABCD, costruito sul triangolo ABD, è equivalente al rettangolo che ha per dimensioni  i cateti del triangolo AED’.

| Home Page Cabri | Torna a FLATlandia | Archivi |