 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Aprile 2003
Il testo del problema:
1) Ritagliare da un cartoncino due triangoli rettangoli scaleni fra loro congruenti ed un terzo triangolo rettangolo, che, unito ai primi due come in un puzzle, formi un trapezio non rettangolo (per trapezio si intenda un quadrilatero con due lati paralleli e gli altri due non paralleli).
2) Considerato uno dei possibili trapezi così costruiti ed indicate con a, b, c le misure dei cateti e dell’ipotenusa dei due triangoli rettangoli congruenti, trovare il rapporto fra i lati obliqui di tale trapezio.
3) Si chiede inoltre se è possibile individuare a, b, c in modo che il trapezio considerato nel punto precedente abbia le dimensioni espresse da numeri interi.
Giustificare le costruzioni e motivare le risposte.
Commento
Figure e commenti proposti da:
Valeria Cua, Andrea Maida e Marco Zetti
Classe 3P, Scuola Media di S. Genesio (PV).
|
FIG.1: Costruisco il triangolo rettangolo scaleno ABC e il suo simmetrico rispetto al cateto maggiore, chiamo P il simmetrico di A. Traccio la parallela ad AP passante per B e la perpendicolare a BP passante per P. Ottengo il trapezio ABDP. |
FIG.2: Costruisco il triangolo ABC e il suo simmetrico rispetto al cateto minore, chiamo D il simmetrico di A. Traccio la parallela a BD passante per A. Traccio la perpendicolare a DA passante per D. Chiamo P il punto in cui si incontrano. Ho ottenuto il trapezio ABDP |
||
|
FIG.3: Ho costruito il
triangolo ABC e ho trovato il corrispondente di ABC nella simmetria centrale
con centro il punto medio di BC. Chiamo P il simmetrico di A. |
FIG.4: Ho costruito il triangolo rettangolo ABC e ho ottenuto il triangolo PCD congruente ad ABC traslando ABC di un vettore uguale a BC. Ora, per trovare il terzo triangolo rettangolo congiungo i vertici degli angoli retti. Il triangolo APC è rettangolo perché gli angoli ACB e PCD cono complementari. I segmenti AP e BD sono paralleli perché le altezze AH e PK sono congruenti essendo altezze relative all’ipotenusa di triangoli congruenti. Il terzo triangolo ottenuto è congruente ai primi due. [[…]] |
||
|
|
FIG.5: Abbiamo costruito il triangolo rettangolo scaleno DHA poi il suo simmetrico rispetto al cateto maggiore DH. Il punto B è il simmetrico di A. Abbiamo tracciato la parallela a DA passante per B e la perpendicolare a DB passante per D e abbiamo chiamato C il punto d’incontro tra le rette. La figura ABCD è un trapezio perché ha due lati paralleli (AD e BC) |
||
Prima di parlare del problema di Aprile vi comunichiamo
che ci sono pervenute per ora due risposte al quesito di Marzo dalle seguenti
scuole:
SM "C. A. Dalla Chiesa", S. Genesio ed Uniti (PV)
ITAS "Pastori", Brescia (BS)
Attendiamo, come detto in precedenza, la fine di Maggio per commentare queste
risposte, in modo da poter accogliere eventuali altre soluzioni di chi volesse
cimentarsi su quel quesito di geometria nello spazio.
Per il problema di Aprile abbiamo ricevuto sette risposte dalle seguenti scuole:
Nel problema proposto si chiedeva di
costruire un trapezio (non rettangolo) utilizzando tre triangoli rettangoli di
cui due, fra loro congruenti, erano assegnati. Avevamo suggerito di ritagliare i
due triangoli dati da un cartoncino; non sappiamo se i ragazzi di S. Genesio
abbiano usato carta e forbici e poi tradotto le loro manipolazioni in disegni
Cabri, tuttavia sono stati quelli che hanno presentato il maggior numero di modi
per ottenere il trapezio:
quattro diverse costruzioni sono state individuate da alcuni alunni della classe
3P, a cui se ne aggiunge una quinta fra quelle trovate dalla classe 2P.
Si proponeva poi di scegliere uno dei trapezi per determinare il rapporto fra i
suoi lati obliqui e di individuare una terna di numeri, per i due triangoli
assegnati, in modo che i lati di tale trapezio avessero misure intere.
Domande molto facili che potevano però portare a scoprire che in una delle
possibili costruzioni (vedere la n° 5 di quelle a corredo del testo nel sito) i
tre triangoli rettangoli non sono simili (o congruenti) come accade nelle altre
figure, per cui non era possibile rispondere alle due domande con procedimenti
di geometria elementare.
Al terzo punto bastava rispondere proponendo una terna pitagorica, trovata anche
in modo empirico; tale risposta poteva risultare più o meno semplice o
addirittura banale, a seconda della figura considerata. I ragazzi del LS "L. da
Vinci" hanno elaborato, per una figura da loro scelta, una bella risposta
fornendo un criterio generale, applicabile anche ad altre situazioni.
Nelle soluzioni pervenute si riscontrano imprecisioni e/o incompletezze per cui abbiamo convenuto di presentare le parti più significative di alcune di esse, in modo da dare un quadro completo delle risposte inviate.
Per illustrare il testo del problema utilizzeremo le costruzioni inviate dalla scuola media di S. Genesio, corredate dalle loro descrizioni (vedi sopra)
Pubblichiamo le seguenti risposte:
Scuole medie inferiori
Scuole superiori
NOTA: come di consueto le correzioni o le osservazioni
sono racchiuse in parentesi quadra; con doppia parentesi quadra si indicano le
parti omesse.
SOLUZIONI
Soluzione proposta da:
Classe 2^A - Scuola Media di Roveredo in Piano (PN)
1)
1. Punti A, B;
2. punto medio tra A e B: O;
3. circonferenza k di centro O passante per A;
4. triangolo [scaleno] ABC con C su k (il triangolo è rettangolo perché
inscritto in una semicirconferenza).
5. punto medio del lato AC:M;
6. simmetria centrale del triangolo ABC rispetto M (A'B'C') (i vertici A', C'
coincidono rispettivamente con C e con A).
Abbiamo disegnato due triangoli rettangoli congruenti, metà del quadrilatero
ABCB' che risulta essere un parallelogramma (ogni parallelogramma ha come centro
di simmetria il punto medio delle diagonali).
Caso a)
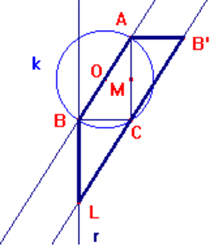
Tracciamo le rette per BA e CB' (sono parallele perché
contengono lati opposti di un parallelogramma) e la retta r perpendicolare al
lato BC passante per B; facciamo l'intersezione ( L) di r con la retta B'C e
otteniamo il triangolo BCL congruente con gli altri due triangoli (i triangoli
BCL e AB'C sono congruenti avendo due angoli ed il lato compreso congruenti:
lato BC congruente con AB', lati opposti di un parallelogramma; gli angoli di
vertice B e A sono retti, gli angoli di vertici C e B' sono congruenti essendo
[angoli corrispondenti formati da] i lati BC e AB' paralleli ed i lati CL e B'C
[che] stanno sulle stessa retta).
Il testo non esclude esplicitamente che il terzo triangolo rettangolo non possa
essere congruente con gli altri due, ma crediamo che il senso del testo non sia
questo.
Caso b)
Dopo l’operazione 6.
Tracciamo: le rette che contengono i lati opposti del parallelogramma AB' e BC
(parallele), la retta s perpendicolare al lato CB' passante per B' e la sua
intersezione con la retta BC (D).
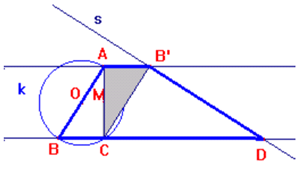
2)
caso b)
Il triangolo CB'D è simile al triangolo ACB' (gli angoli
di vertici B' e C del triangolo CDB' sono congruenti con i rispettivi angoli di
vertici A e B' del triangolo CB'A: i primi sono retti, i secondi sono alterni
interi se consideriamo le due rette parallele che contengono i lati AB' e BD
tagliate dalla retta che passa per CB').
Indichiamo con: a, il cateto BC e AB'; b, il cateto AC ; c, l'ipotenusa AB e CB'
dei triangoli rettangoli ABC e CB’A. Consideriamo i lati del triangolo CDB': il
cateto CB' coincide con l'ipotenusa dei triangoli rettangoli congruenti, quindi
è c; per il cateto DB' vale la seguente proporzione, AC : DB' = AB' : CB' : cioè
b : DB' = a : c da cui DB' = b*c/a, consegue che il rapporto BA/DB' = a/b
3)
[[…]]
Soluzione proposta da:
Classe 3A, Scuola Media di Rolo (RE)
Sezione staccata dell'I.C. "I. Calvino" di Fabbrico e Rolo
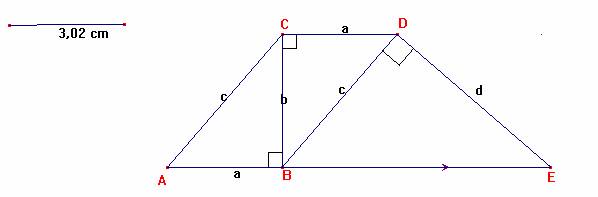
1) Con CABRI II abbiamo costruito i due triangoli rettangoli congruenti ABC e BCD e li abbiamo disposti in modo che coincidano i cateti congruenti BC, ottenendo così il parallelogrammo ABDC. Poi abbiamo tracciato la retta per D perpendicolare a DB e la retta per B parallela a DC, E è il punto di intersezione delle rette. ACDE è il trapezio richiesto.
2) Abbiamo scoperto che i triangoli ABC e BDE sono simili per l'evidente congruenza degli angoli acuti [è più corretto precisare quali e perché], (parallele AE e CD tagliate dalla trasversale BD). Possiamo quindi scrivere la proporzione che esprime l'uguaglianza dei rapporti fra i cateti dei due triangoli a : b = c : d da cui si deduce che il rapporto fra i lati obliqui del trapezio è uguale al rapporto fra i cateti del triangolo iniziale.
3) I lati del trapezio sono numeri interi se a,b,c costituiscono una terna pitagorica (derivata) in cui l'ipotenusa "c" è un multiplo del cateto "a", questo si deduce dalla proporzione precedente [essendo d = b*c/a è il prodotto b*c che deve essere multiplo di a].
Soluzioni proposte da:
Leone Cesare Cimetta - Classe 1F, LS “Leonardo da Vinci” TV
Visto il gran numero di formule matematiche Per maggior completezza pubblichiamo le soluzioni proposte da Cimetta sotto forma di file PDF da scaricare (è richiesto Adobe Acrobat per visualizzare il file).
Soluzioni proposte da:
Classe 1Bst ITI "Berenini" Fidenza (PR)
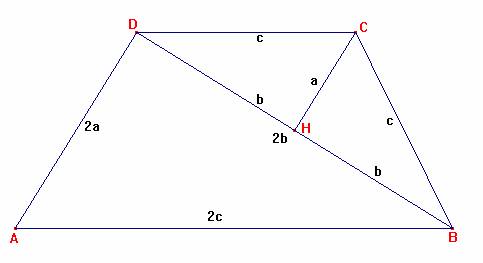
1° Parte:
Disegnare due triangoli rettangoli congruenti DCH e BHC con il cateto minore CH
in comune.
Disegnare un altro triangolo, rettangolo in D e simile ai primi due, ma con le
misure dei lati doppie e con il cateto maggiore DB formato dai cateti maggiori
DH e HB dei due triangoli congruenti.
La figura così ottenuta è un trapezio [occorre precisare perché] scaleno
[potrebbe essere isoscele nel caso particolare in cui sia c = 2a].
2° Parte:
Dalla similitudine dei triangoli ADB e DHC costruiti al punto 1), si ha la
proporzione
AD : CH = DB : HB = 2 : 1 e quindi AD = 2a. Perciò il rapporto tra i lati
obliqui del trapezio è
AD/BC = 2a/c.
3° Parte:
Poiché sqrt(3^2 + 4^2) = 5 , c = 5 , a = 3 e b = 4.
| Home Page Cabri | Torna a FLATlandia | Archivi |