
Blaise Pascal
Sulle orme di Desargues

Cinque anni dopo la morte della moglie, il padre di Pascal lasciò Clermont per stabilirsi a Parigi, dove i profitti dei suoi investimenti gli garantirono una vita confortevole. A Parigi, Étienne entrò nell'Accademia fondata da Mersenne, e all'età di quattordici anni, Blaise iniziò ad accompagnare suo padre alle riunioni settimanali. Qui, oltre a Mersenne, il giovane Pascal incontrò alcuni tra i più importanti scienziati parigini, come Gassendi, Roberval, Carcavi, Mydorge e Desargues, da cui imparò molto.
Nel 1639, quando Desargues pubblicò il Brouillon project, Blaise ne assimilò rapidamente il contenuto e l'anno successivo presentò il suo Essay pour les coniques all'Accademia di Mersenne. Molto probabilmente fu proprio lo stesso Desargues ad incoraggiare il giovane Pascal a pubblicarlo nel 1640. Nel suo saggio, Pascal delineò brevemente il programma che intendeva sviluppare per un nuovo e più completo trattato sulle sezioni coniche, a cui si riferiva con il nome di Conicorum opus completum.
Nelo anno, il padre di Blaise fu nominato esattore delle tasse del re per l'Alta Normandia, così la famiglia Pascal lasciò Parigi e si stabilì a Rouen dove Blaise continuò a lavorare sul suo trattato sulle sezioni coniche. Occasionalmente tornò a Parigi con suo padre e durante i suoi brevi soggiorni nella capitale fu in grado di presentare le sue scoperte all'accademia di Mersenne.
Nel 1642, Desargues era desideroso di vedere la dimostrazione di un importante teorema, che chiamò "la Pascale", da cui, secondo il suo parere, "i quattro libri di Apollonio erano una conseguenza immediata". Due anni più tardi, nella prefazione della sua Cogitata physico-mathemaica, Mersenne concentrò l'attenzione su "una singola proposizione molto generale con la quale Pascal poteva stabilire quattrocento corollari che coprivano ogni campo del trattato di Apollonio". Il 17 marzo 1648, Mersenne annunciò a Constantijn Huygens che Pascal aveva finito di scrivere un importante trattato sulle sezioni coniche dicendo:
Tra il 1653 e il 1654 Pascal lavorò ancora al Conicorum opus completum per poi presentare, nello stesso anno, un riassunto delle sue opere all'accademia di Mersenne. Sfortunatamente nel 1659 Pascal si ammalò gravemente, e quando nel 1661 sua sorella Jacqueline morì, la sua condizione emotiva peggiorò notevolmente. Lo stile di vita di Pascal divenne sempre più ascetico, convinto del fatto, che la sofferenza e la malattia fossero lo stato naturale per tutti i cristiani. Il mattino del 19 agosto del 1662, a causa di gravi convulsioni, si spense alla giovane età di 39 anni.Se il vostro Archimede verrà con voi, gli mostreremo uno dei migliori trattati geometrici che abbia mai visto, che è stato completato dal giovane Pascal. è la soluzione al locus delle 3 e 4 rette di Pappo, che qui si dice non sia stato risolto in tutta la sua generalità da Cartesio. Ci sono volute rette rosse, verdi, nere, ecc. per distinguere la varietà di considerazioni...

Per quanto riguarda il trattato sulle sezioni coniche di Pascal, la storia è un po' più complessa.Abbiamo molti altri problemi, teoremi, e conseguenze dei precedenti ma, la poca fiducia che ho in me stesso, per la mia mancanza di esperienza e capacità, non mi permette di avanzare ulteriormente. Potrò procedere solo dopo che l'opera verrà esaminata da persone abili; Se giudicheremo che merita di essere continuato, cercheremo di spingerlo fino a dove Dio ci darà la forza.
Nel 1673, Henry Oldenburg, segretario della Royal Society di Londra, fu informato dell'esistenza di un manoscritto di Pascal. Il 6 aprile, Oldenburg, sempre desideroso di seguire gli sviluppi della matematica francese, scrisse a Gottfried Wilhelm Leibniz, che si trovava allora a Parigi, chiedendogli di indagare su quel manoscritto, in modo che potesse essere riportato alla luce. Intervenne allora Leibniz che riuscì ad ottenere il permesso dagli eredi, di vedere i manoscritti geometrici di Pascal, che gli furono tuttavia consegnati in due momenti differenti. Tuttavia il manoscritto del trattato sulle sezioni coniche non fu nelle mani di Leibniz fino alla fine del 1675. Leibniz esaminò con cura il trattato di Pascal, prendendo alcune note su fogli separati, copiandone solo la prima parte. Il 30 agosto 1676, restituendo i manoscritti agli eredi, scrisse una lettera a Florin Périer, marito della sorella maggiore di Pascal. Dalle sue parole si evince che non aveva letto il manoscritto molto approfonditamente, infatti scrisse:
Mi sarebbe comunque piaciuto poterli leggere con un po' più di attenzione ma, le tante distrazioni che non mi hanno permesso di disporre completamente del mio tempo, non lo hanno permesso. Tuttavia, credo di averle lette abbastanza per essere in grado di soddisfare la vostra richiesta, e per dirvi che ritengo il lavoro finito e pronto per la pubblicazione.
Successivamente, Leibniz descrisse brevemente le sei parti, in cui pensò che il manoscritto avrebbe potuto essere organizzato per la stampa. La Generatio conisectionum, ovvero la copia che Leibnitz trasse dalla lettura della prima parte del trattato di Pascal, inizia con le definizioni di superficie conica, a base circolare, e dei suoi elementi vertice, pendenza e generatrice ossia le stesse definizioni che Desargues diede nel Brouillon project nel 1639. All'interno dell'opera troviamo ovviamente le definizioni dei sei tipi di sezioni coniche, diversi corollari (tra i quali molti riguardanti le immagini delle secanti e delle tangenti della circonferenza del cono di base nel piano di sezione) e i due concetti "proiettivi" di punti senza immagine e di punti mancanti.
Leibniz diede il titolo: De hexagrammo Mystico et Conico alla seconda parte del trattato di Pascal. Dopo aver discusso la generazione ottica di sezioni coniche come proiezione di un cerchio in un piano (il piano di sezione del cono), Pascal introdusse, in questa parte, la figura notevole composta da sei rette ossia una particolare configurazione che chiamò Hexagrammum Mysticum.
Secondo Leibniz, fu usando la proiezione che Pascal mostrò che ogni esagramma mistico "appartiene" ad una sezione conica, e che, viceversa, ogni sezione conica dà luogo ad un esagramma mistico. Inoltre Leibniz osservò che, la mancanza di figure in questa parte fu compensata dalle figure inserite nella sesta parte.
Leibniz pensò che la terza parte si sarebbe dovuta chiamare De quatuor tangentibus, et rectis puncta tactuum jungentibus, unde rectarum harmonice sectarum et diametrorum proprietates oriuntur. Leibniz osservò che fu qui che Pascal spiegò l'uso dell'esagramma mistico per trovare le proprietà dei centri e dei diametri delle sezioni coniche sottolineando che non sembrava mancare nulla.
Proseguendo, secondo Leibniz, la quarta parte avrebbe dovuto essere intitolata De propositionibus segmentorum secantium et tangentium e avrebbe dovuto trattare di ordinate, e rapporti di segmenti intercettati su una retta da una sezione conica. Di questa parte Leibnitz disse solo che diverse figure erano incluse nella trattazione e che non sembrava mancare nulla.
La quinta parte, secondo Leibnitz, avrebbe dovuto essere intitolata De tactionibus conicis, cioè, come spiegò, "sui punti di contatto e tangenti ad una sezione conica". Si ritiene che questa quinta parte trattasse i sei problemi classici riguardanti la costruzione di coniche che passano attraverso \( 5-n \) punti e tangenti a \( n \) rette date in posizione, per \( 0 \le n \le 5 \). è altamente probabile che Pascal affrontò questi problemi, anche perché la costruzione della sezione conica che passa attraverso cinque punti specifici era già stata trattata da Mydorge nel 1637.
Alla sesta parte, che Pascal lasciò senza titolo, Leibniz diede il nome di De loco Solido, sottolineando che si trattava dello stesso soggetto su cui Cartesio e Fermat avevano già lavorato, cioè il problema di Pappo delle tre e quattro rette. Leibniz osservò che quest'ultima parte includeva molte definizioni e risultati, già spiegati nella seconda parte, in particolare, conteneva la definizione e le proprietà dell'Hexagrammum conicum mysticum, illustrato da diverse grandi figure colorate.
Fu forse il lemma XIII del settimo libro della Collezione di Pappo, noto come Teorema di Pappo a dare qualche suggerimenti a Pascal: Enunciato:
Fu forse un'analisi approfondita del Brouillon project di Desargues a convincere Pascal che uno studio diretto delle sezioni coniche potesse essere fondato sulla semplice idea che cinque punti in posizione generale in un piano, determinassero un'unica conica e che la condizione che un sesto punto si trovasse su quella curva desse una relazione che poteva essere usata come definizione comune per tutti i tipi di sezione conica.Se \( A, E, B\) sono tre punti collinari e \( C, F, D \) sono altri tre punti collinari, allora i punti di intersezione \(G, M, K\), delle coppie di linee \(AF\) e \(EC\), \( AD \) e \( BC \), \( ED \) e \( BF \) sono collinari.
Ma, poiché la relazione legata a quest'ultimo risultato era troppo difficile da applicare, Pascal cercò una relazione più semplice che potreva essere espressa anche graficamente, con l'obiettivo di applicare il metodo della proiezione. Cercando una tale condizione, Pascal prese un cerchio e sei punti posti regolarmente su di esso e si rese conto che le tre coppie di lati opposti si intersecavano in altri tre punti collinari. Pascal applicò nuovamente la costruzione per altri esagoni inscritti nel cerchio e i disegni confermarono l'intuizione.
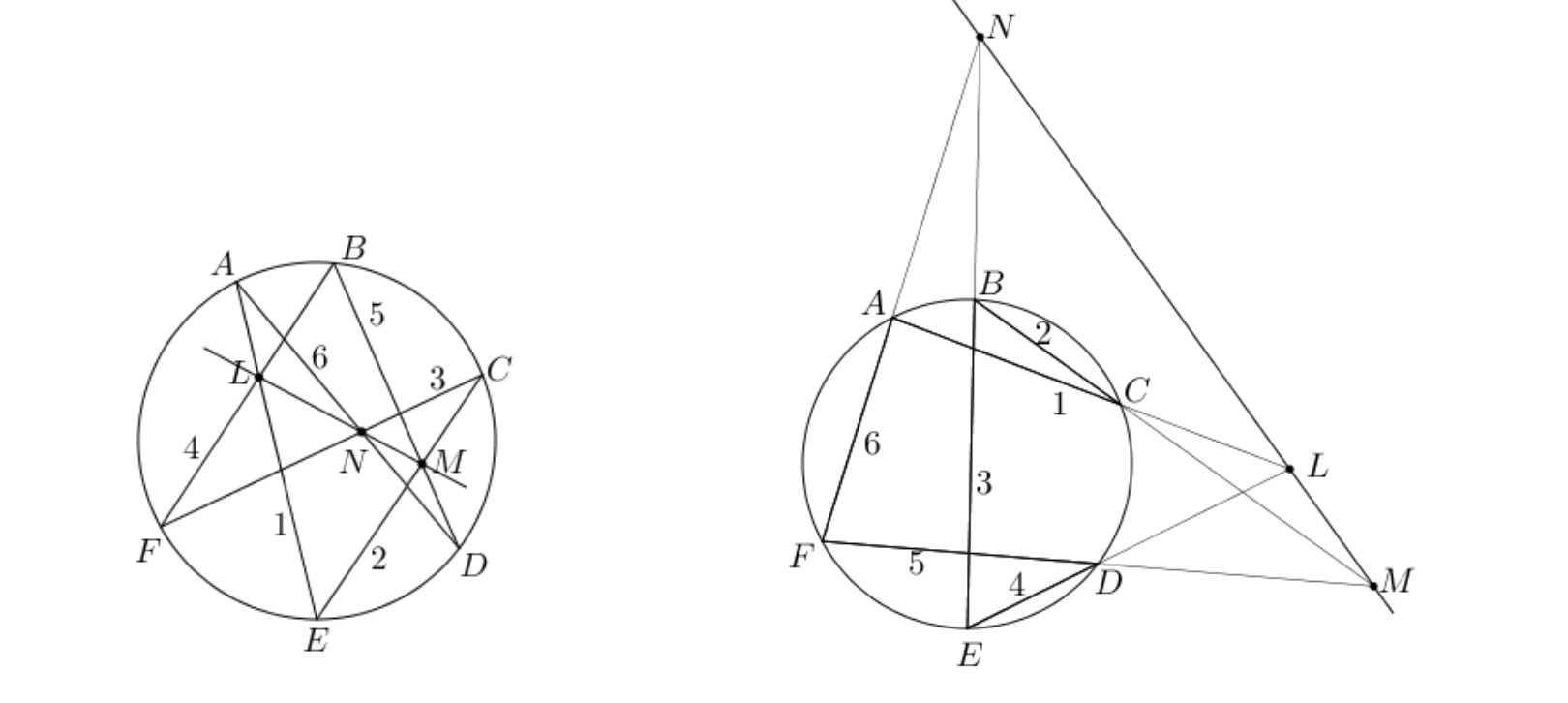
E' possibile trovare una dimostrazione di questo teorema, nel link adiacente a pagina 21-22: Testo completo
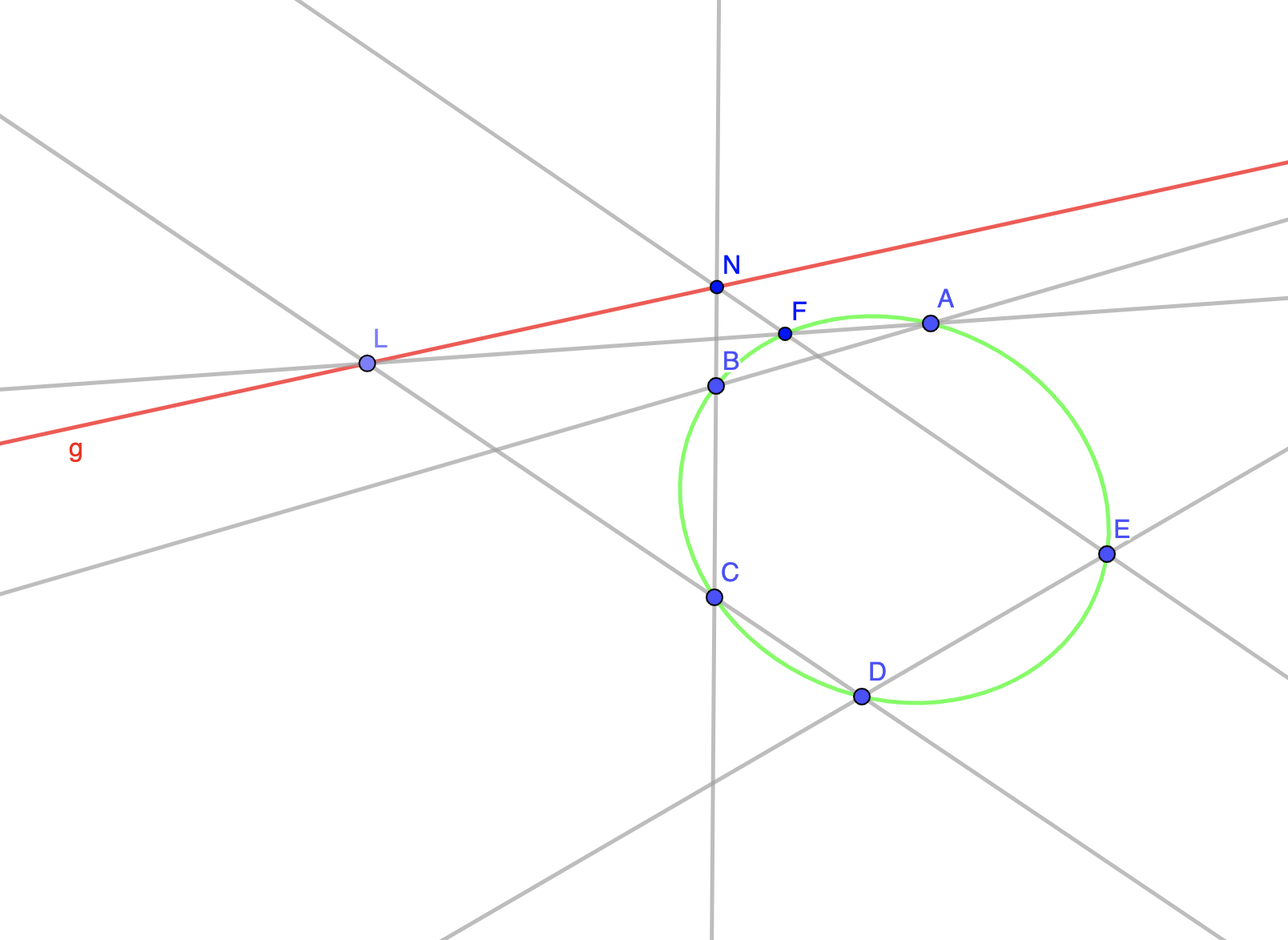
Dati i punti \( A, B, C, D, E \), tre dei quali non sulla stessa retta, si disegnano le rette \( AB, BC, CD, DE \), poi dal punto \( M \) generato dall'intersezione di \( AB \) e \( DE \), si traccia una retta \( g \) che interseca le rette \( CD \) e \( BC \) rispettivamente in \( L \) e \( N \). Infine si tracciano le rette \( LA \) e \( NE \). Il punto \( F \), intersezione di \( LA \) e \( NE \) appartiene necessariamente all'unica sezione conica che passa attraverso i cinque punti indicati. Ecco che in questo modo abbiamo ottenuto una costruzione della conica passante per cinque punti. Questa costruzione è nota anche con il nome di: Teorema di Braikenridge e Maclaurin.
Clicca qui per la costruzione della conica per 5 punti con GeoGebra
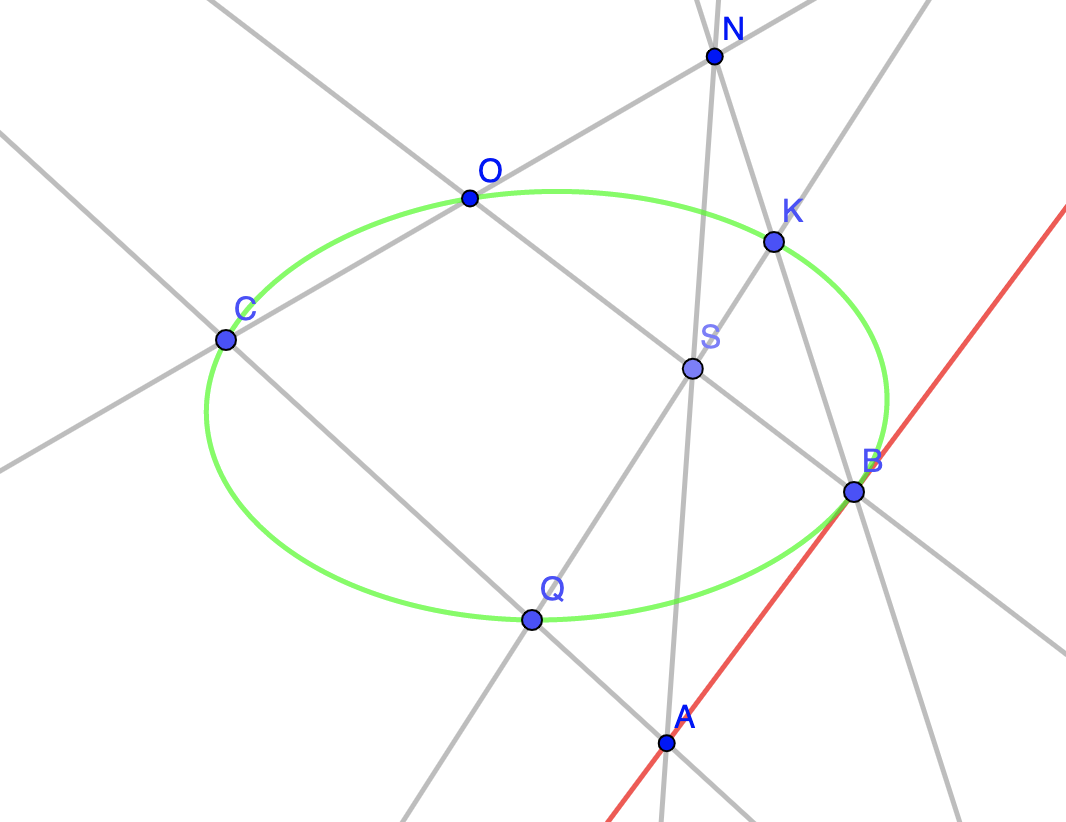
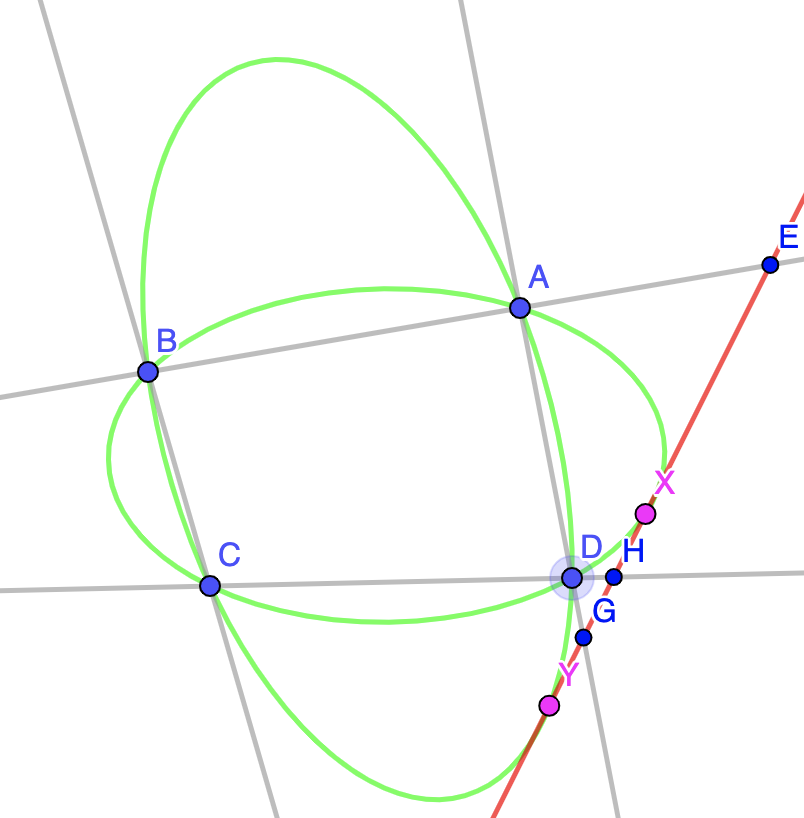
$$ \biggl( \frac{GX}{EX} \biggr)^2=\frac{HG}{HE}\times\frac{GF}{EF} $$.
Quest'ultima relazione ci permette di determinare la posizione del punto \(X\) (ovviamente, ci sono due soluzioni per questo problema).
Possiamo sbilanciarci ed affermare che nei casi: tre punti e due tangenti ed un punto e quattro tangenti, Pascal ragionò in maniera del tutto analoga.
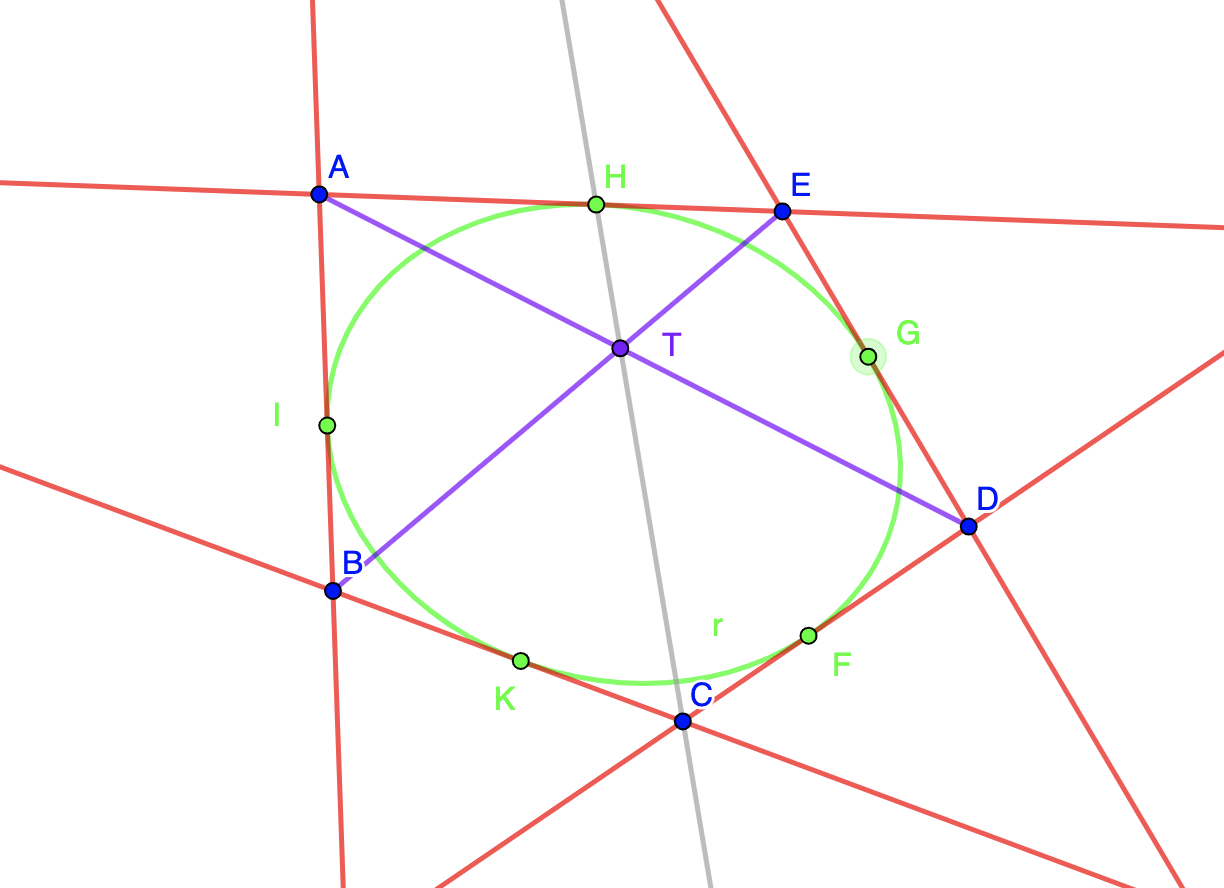
Quindi se \( a, b, c, d, e \) sono le rette date, per trovare il punto \( H \) in cui \( a \) interseca la sezione conica che stiamo cercando, è sufficiente determinare il punto \( T \), intersezione di \( AD \) con \( BE \), e intersecare \( CT \) con \( a \). In modo del tutto analogo possiamo determinare tutti gli altri punti di contatto.
Clicca qui per la costruzione della conica tangente a cinque rette date con GeoGebra