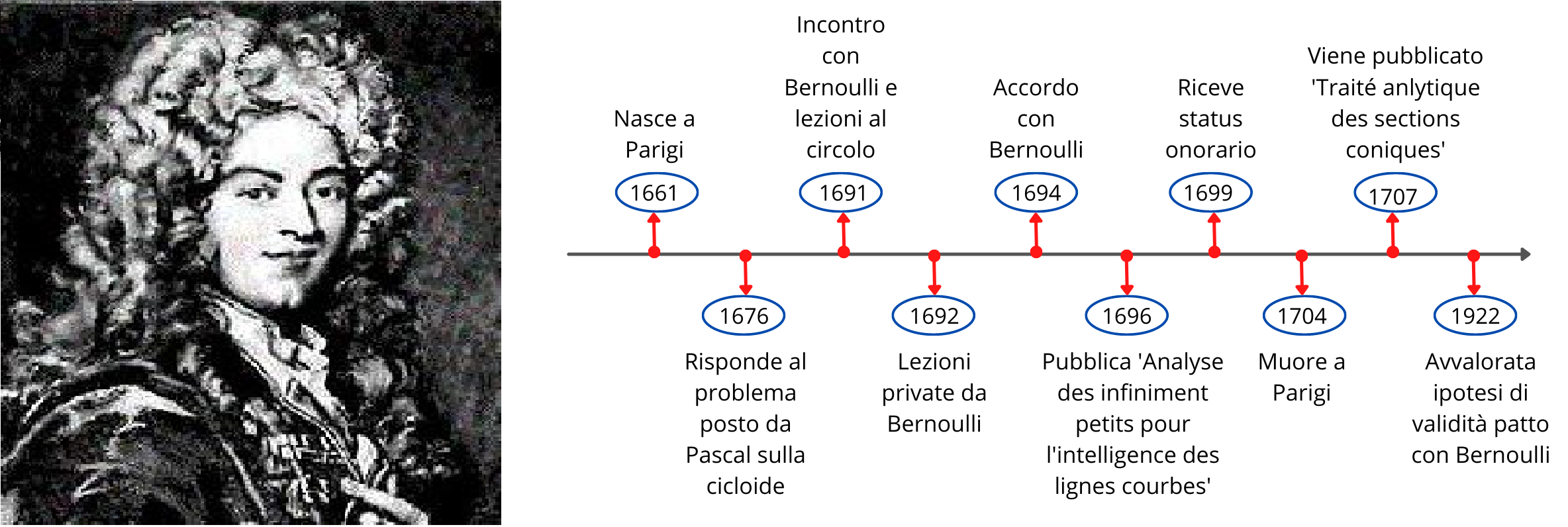
Guillaume François de l'Hôpital nasce a Parigi nel 1661 in una famiglia molto importante di Francia. Fin da bambino sviluppa grandi capacità matematiche e una vera passione per la materia. Si racconta che a 15 anni risolse un problema molto difficile sulla cicloide che Blaise Pascal (1623-1662) aveva proposto. Nonostante questa passione e il talento, intraprese la carriera militare seguendo le orme del padre, ma ben presto, a causa di una grave miopia, egli dovette rinunciare a tale incarico, anche se, forse, l'amore per la matematica piuttosto che l'imperfezione della vista fu all'origine della decisione.

Nel 1696 L'Hôpital pubblica Analyse des infinimentpetits pour l'intelligence des lignes courbes, che rappresenta il primo libro di testo sul calcolo differenziale. Nell'introduzione l'Hôpital riconosce il suo debito verso Leibniz, Jacob e Johann Bernoulli, Newton, ma il concepimento dell'opera è certamente merito suo. Soltanto dopo la morte di l'Hôpital, Bernulli sostiene che il libro è essenzialmente opera sua e svela il patto tra i due. Le sue rivendicazioni vengono confermate nel 1922, dopo il ritrovamento dei manoscritti del corso tenuto da Bernoulli a l''Hôpital.
L'opera è suddivisa in 10 sezioni in cui sono riportate le regole del calcolo differenziale e il loro utilizzo nella risoluzione di alcuni problemi.
L'Hôpital muore a Parigi nel 1704. Nel 1707 viene pubblicata una sua opera rimasta inedita: Traité analytique des sections coniques et de leur usage pourla resolution des equations dans les problemes tant déterminezqu'indéterminez.

L'opera è suddivisa in 10 libri, al cui interno viene sviluppata l'intera teoria delle sezioni coniche, contenuta nei primi 4 libri di Le Coniche di Apollonio, che viene applicata alla risoluzione di problemi determinati e indeterminati. L'Hôpital inizia definendo parabola, ellisse e iperbole nello stesso modo in cui vengono definite oggi (tramite i fuochi e la proprietà fuoco-direttrice). L'opera è interamente di geometria analitica, tranne il sesto libro, che utilizza il metodo delle proiezioni. Si pensa che tale libro sia stato scritto da Le Poivre, uno dei due geometri che aiutarono il tipografo nella impaginazione e sistemazione dell'opera manoscritta.
L'Hôpital enuncia il Teorema delle Corde per la prima volta nel quarto libro del trattato sulle sezioni coniche (1707). La formulazione è la seguente:
Teorema delle Corde: Sono date due corde MN e AR di una sezione conica, che si incontrano in P e sono parallele a due rette date in posizione. Allora il rettangolo PMxPN sta sempre al rettangolo APxPR in un dato rapporto, qualunque sia la loro posizione rispetto alla sezione conica.
L'Hôpital fornisce dimostrazioni analitiche separate distinguendo il caso della parabola da quello delle coniche con centro (ellisse e iperbole).
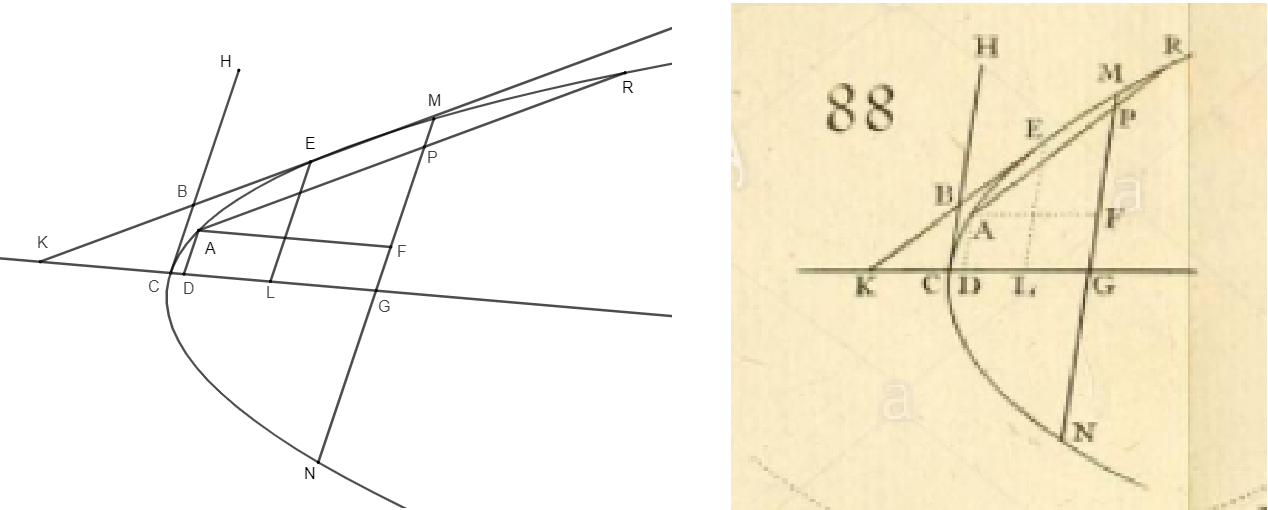
Per dimostrare il teorema nel caso delle coniche centrali, l'Hôpital procede in modo simile ma fornisce dimostrazioni diverse per ogni tipo di conica. L'Hôpital, inoltre, deduce i seguenti risultati direttamente dal Teorema delle Corde:
Jacques-François Le Poivre nasce a Mons, in Belgio nel 1652, e muore nel 1710. Non si hanno molte notizie sulla sua vita, o sulla sua infanzia. Studia la gnomonica, un ramo dell'astronomia, e si interessa alla geometria di Cartesio.
Nel 1706 pubblica un trattato sulla gnomonica che andò perduto. In quell'anno lavora anche come sovrintendente civico all'edilizia.
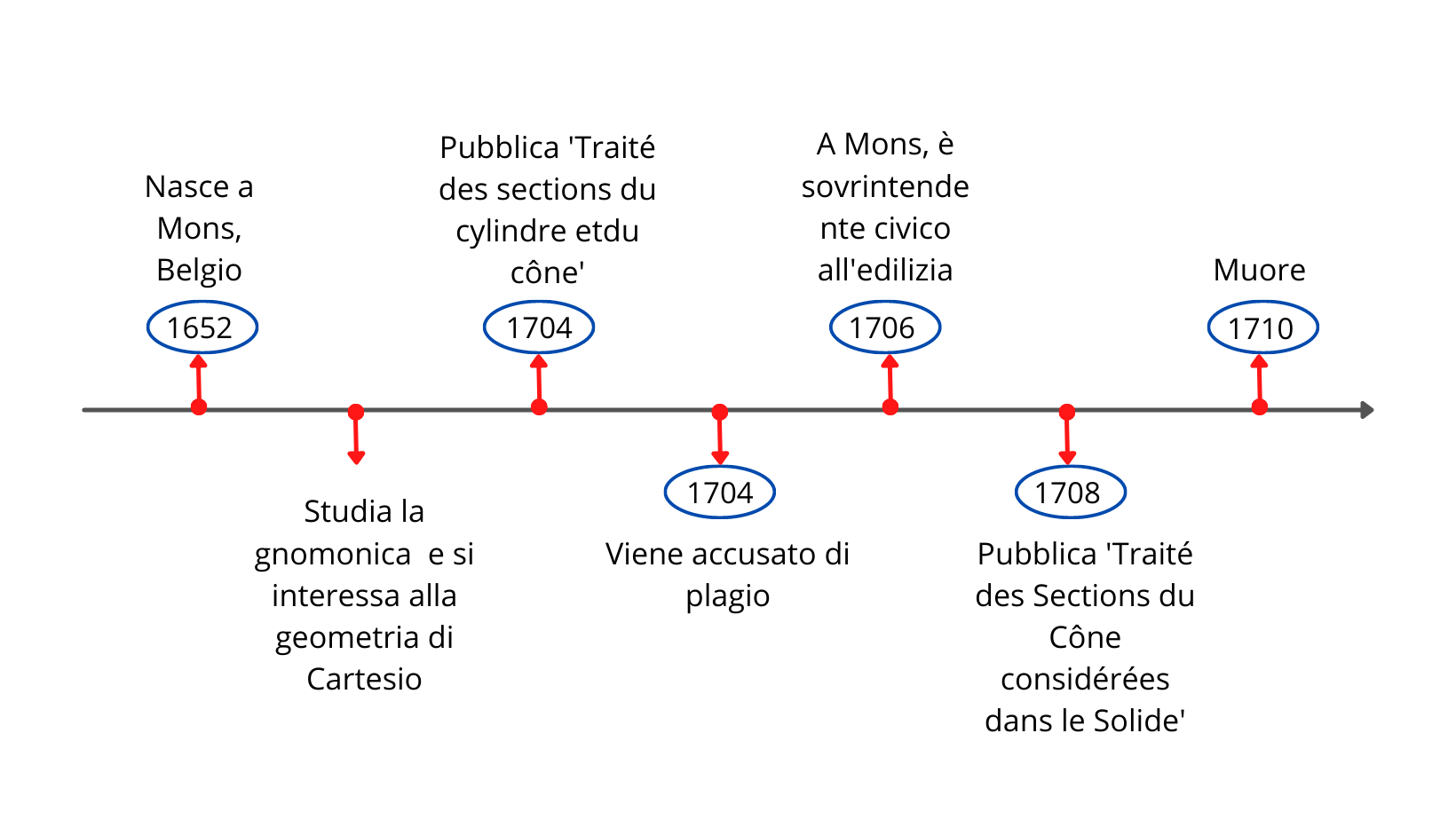
Le Poivre nel 1704 pubblica Traité des sections du cylindre et du cône, considérées dans le solide et dans le plan, avec des démonstrations simple et nouvelle.
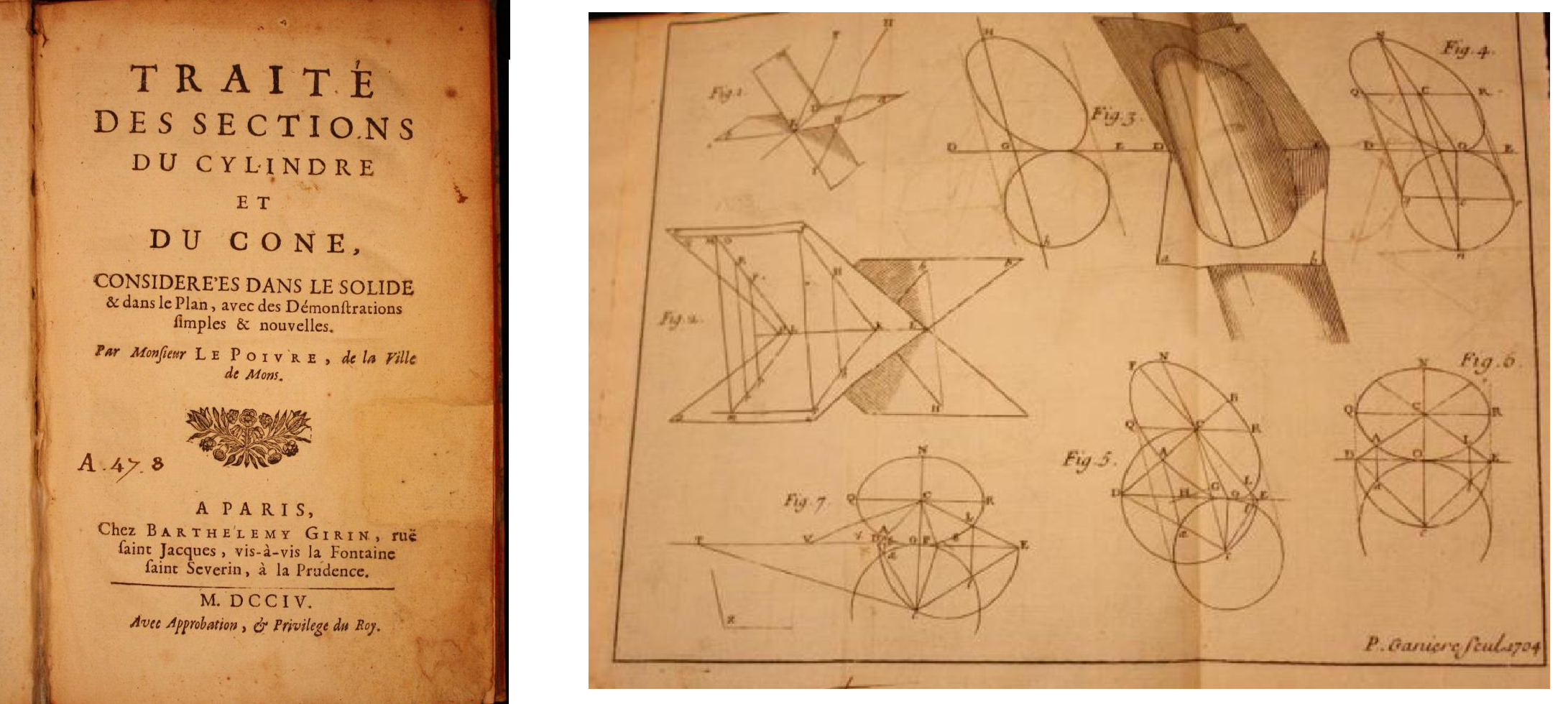
L'opera è concisa, di 61 pagine dove Le Poivre presenta uno studio delle sezioni coniche attraverso il metodo delle proiezioni, in particolare, passando nello spazio, fornisce una dimostrazione geometrica semplice e diretta del Teorema delle Corde.
Le Poivre viene accusato di plagio da un anonimo recensore che pubblica una recensione dell'opera sul Journal des Savants. Per smentire l'accusa, Le Poivre pubblica nel 1708 del Traité des Sections du Cône considérées dans le Solide, Avec des démonstrations simples & nouvelles, opera in cui dedica molte pagine al controbattere meticolosamente le osservazioni del recensore.

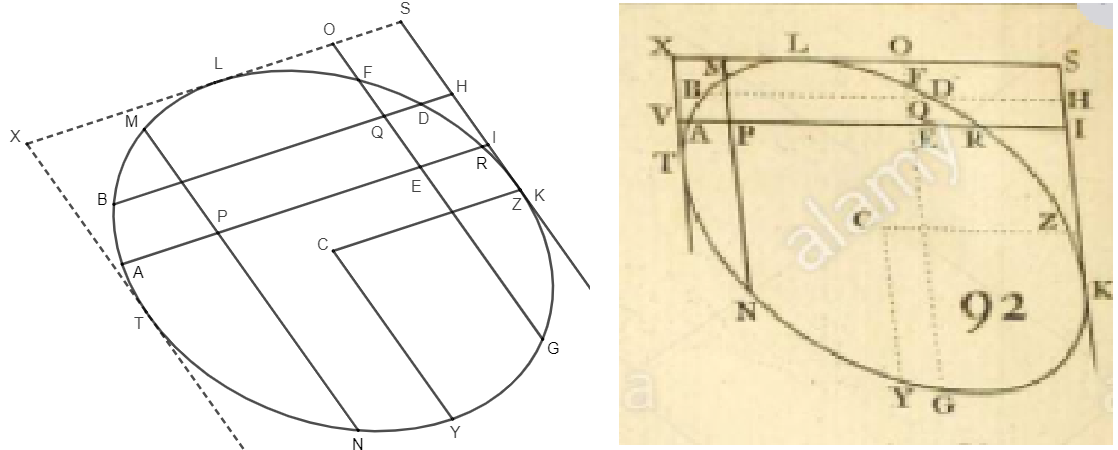
Le Poivre enuncia il Teorema delle Corde nello spazio, la prima volta, nel 1704. L'enunciato riporta:
Teorema delle Corde: Se una retta MN e due paralleli FH e IL, che sono intersecati da MN rispettivamente in G e K, intersecano una sezione conica, i rettangoli FGH e IKL, sottostanti le porzioni degli stessi paralleli sono proporzionali ai due rettangoli MGN e MKN, sottostanti le porzioni dell'altra retta.
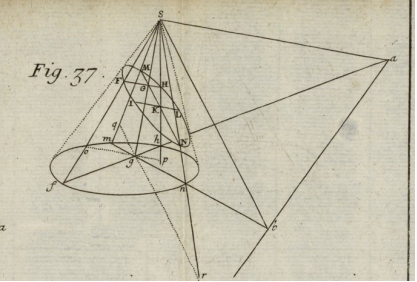
Tale dimostrazione non richiede alcuna nozione o conoscenza delle proprietà dei diametri delle sezioni coniche, ed è la stessa che appare nel sesto libro del trattato di l'Hôpital.
La tesina completa è riportata al seguente link: