Bonaventura Cavalieri:
la prima costruzione lineare delle coniche
a cura di Cristina Munerato
Visualizza documento completo
Bonaventura Cavalieri nasce a Milano nel 1598. All'età di 16 anni entra a far parte dell'ordine dei gesuati di S. Girolamo.
Si reca poi a Pisa, dove conosce Benedetto Castelli (1578-1643), docente di matematica e allievo di Galileo Galilei (1564-1642).
Castelli introduce Cavalieri alla geometria e, riconoscendone le capacità, lo presenta allo stesso Galilei.
Dopo un breve soggiorno a Firenze, decide di trasferirsi a Milano, dove continua a studiare teologia.
In questi anni porta avanti gli studi matematici, in particolare a quelli che lo porteranno alla formulazione della teoria degli indivisibili.
Nel 1629, grazie all'appoggio di Galilei, riesce ad ottenere la cattedra di matematica all'Università di Bologna.
Durante le lezioni universitarie, propone ai suoi studenti gli Elementi di Euclide, la teoria dei pianeti e l'Almagesto di
Claudio Tolomeo (circa 100-175), ma anche argomenti più recenti come la teoria astronomica di Nicolò Copernico (1473-1543).
La prima sua opera, il Directorium generale Uranometricum, pubblicata nel 1632, è un trattato di astronometria, contenente una collezione di tavole
logaritmiche e funzioni trigonometriche con dirette applicazioni ai triangoli.
Nello stesso anno pubblica il suo secondo lavoro dal titolo Lo specchio ustorio, un trattato sulle sezioni coniche,
dove compaiono i primi accenni alla teoria degli indivisibili utilizzata per trattare il moto dei gravi.
Nel 1635 pubblica la Geometria indivisibilibus continuorum nova quadam ratione promota, contenente i principi della teoria degli indivisibili.
La morte di Galilei nel 1642 priva Cavalieri del suo principale interlocutore e, negli anni a seguire, egli si confronta con il matematico Evangelista
Torricelli (1608-1647), successore di Galilei a Firenze, oltre che con il matematico Giovanni Antonio Rocca (1607-1656).
Durante l'ultimo periodo della sua vita, porta avanti una controversia con il gesuita svizzero Paul Guldin (1577-1643) riguardante la teoria
degli indivisibili, di cui si ha testimonianza nella Trigonometria plana et sphaerica, linearis et logarithmica, pubblicato nel 1643.
Sfortunatamente il progetto di continuare tale dibattito viene interrotto a causa della morte di Guldin.
Nel 1647 pubblica le Exercitationes geometricae sex, una raccolta di sei libri contenenti diversi problemi ed esercitazioni matematiche.
Durante tutta la sua vita soffre di gotta, che lo porta a difficoltà nel camminare e scrivere, in particolare durante i suoi ultimi anni.
Pochi giorni dopo la pubblicazione della sua ultima opera, Cavalieri muore a Bologna, nel 1647.
Un primo approccio allo studio delle sezioni coniche da parte del matematico risale al 1623, quando, volendo applicare la teoria degli indivisibili alla
quadratura della spirale di Archimede, si imbatte in una costruzione della parabola.
Tale costruzione è contenuta nella Geometria indivisibilibus continuorum nova quadam ratione promota, pubblicata nel 1635, ed è la prima costruzione
mai presentata che utilizzi solamente linee rette, andando così a sfatare quel mito degli antichi, in base al quale le coniche potevano essere costruite
solamente con l'utilizzo del compasso.
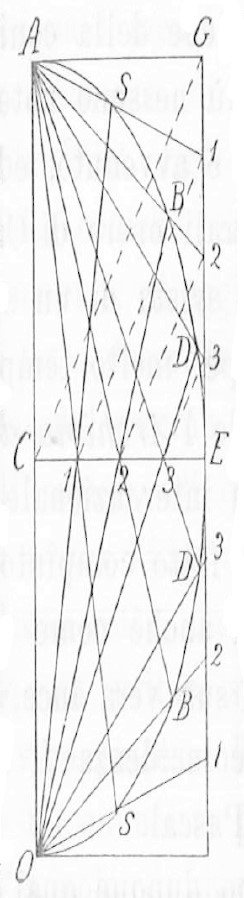
Costruzione lineare della parabola senza compasso
Dati \(A\) il vertice della parabola, \(AC\) l'asse, \(AG\) la tangente al vertice ed \(E\) un punto qualunque della curva, si costruisce il parallelogramma
\(ACEG\).
Si traccia la linea tratteggiata \(CG\) e si considerano poi delle parallele a \(CG\) che intersechino i segmenti \(CE\) e \(GE\).
Si individuano quindi i punti contrassegnati \(1,2,3\) su \(CE\) e \(GE\).
Si tracciano le perpendicolari a \(CE\) nei punti \(1,2,3\) e si uniscono i punti sulla retta \(GE\) ad \(A\).
I punti d'intersezione trovati \(A, S, B, D\) ed \(E\) sono punti della parabola.
Successivamente alla pubblicazione della Geometria Indivisibililus, Cavalieri lavora per cercare una costruzione analoga, che non richieda l'utilizzo
del compasso, anche per l'iperbole e l'ellisse.
Pubblica poi tali costruzioni nelle Exercitationes geometricae sex nel 1647.
Costruzione con Geogebra
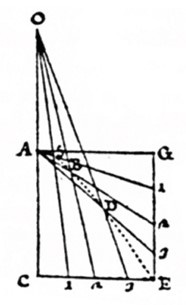
Costruzione lineare dell'iperbole senza compasso
Dati \(A\) il vertice dell'iperbole, \(AC\) l'asse, \(O\) il secondo vertice dell'iperbole, \(AG\) la tangente al vertice ed \(E\) un punto qualunque della curva,
si costruisce il parallelogramma \(ACEG\).
Si traccia \(CG\) e si considerano poi delle parallele a \(CG\) che intersechino i segmenti \(CE\) e \(GE\).
Si individuano quindi i punti contrassegnati \(1,2,3\) su \(CE\) e \(GE\).
Si uniscono i punti sulla retta \(CE\) ad \(O\) e i punti sulla retta \(GE\) ad \(A\).
I punti d'intersezione trovati \(A, S, B, D\) ed \(E\) sono punti dell'iperbole.
Costruzione con Geogebra
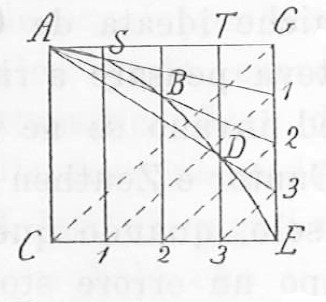
Costruzione lineare dell'ellisse senza compasso
Dati \(A\) un vertice dell'ellisse, \(AO\) l'asse maggiore, \(CE\) metà dell'asse minore si costruiscono i parallelogrammi \(ACEG\) e \(CEHO\).
Si traccia la linea tratteggiata \(CG\) e si considerano poi delle parallele a \(CG\) che intersechino i segmenti \(CE\) e \(GE\).
Si individuano quindi i punti contrassegnati \(1,2,3\) su \(CE\) e \(GE\).
Si uniscono i punti sulla retta \(GE\) ad \(A\) e si tracciano le rette che collegano \(O\) ai punti su \(CE\).
I punti d'intersezione trovati \(A, S, B, D\) ed \(E\) sono punti dell'ellisse.
In modo analogo si individuano i punti \(S',B',D'\).
Costruzione con Geogebra
L'opera principale nella quale Cavalieri tratta le sezioni coniche è Lo Specchio Ustorio overo trattato Delle Settioni Coniche.
Et alcuni loro mirabili effetti Intorno al Lume, Caldo, Freddo, Suono, e Moto ancora, pubblicata nel 1632.
Una prima stesura dell'opera risale al 1627, come testimonia una lettera inviata a Federico Borromeo.
Nell'opera vengono presentate inizialmente alcune definizioni geometriche e dodici proprietà, quattro per ciascuna conica.
I capitoli successivi riguardano problemi di fisica, dove viene dato largo spazio alle proprietà riflettenti degli specchi, in particolare
degli specchi ustori di Archimede, e problemi riguardanti il suono e il moto.
Vi sono anche cenni in merito alla rifrazione delle lenti, alla costruzione del cannocchiale e agli orologi solari.
Gli ultimi capitoli de Lo Specchio Ustorio sono incentrati sulle costruzioni della parabola, dell'iperbole e dell'ellisse tramite l'utilizzo di
strumenti, quali righe, squadre, fili o semplici proporzioni.
Il Cavalieri ci tiene a sottilineare come le costruzioni da lui esposte non siano tutte di sua invenzione, ma riporta solo alcuni tra
i metodi conosciuti all'epoca.
Talvolta apporta alcune modifiche, migliorandone così la comprensione o rendendole più semplici ed eleganti.
Cavalieri suddivide le costruzioni delle coniche in tre gruppi:
- per invention solida, costruzioni meccaniche mediante l'utilizzo di dispositivi mobili nello spazio;
- per invention piana vera, costruzioni meccaniche mediante l'utilizzo di dispositivi mobili sul piano;
- per punti continuati, tramite costruzioni geometriche.
Nell'opera mancano spesso le figure delle costruzioni alle quali fa riferimento, in quanto il matematico predilige soffermarsi sulla motivazione e sul
procedimento di tali costruzioni, piuttosto che sull'aspetto pratico.
Un primo metodo da lui proposto vede l'utilizzo di un cono fisico.
Tale costruzione fa uso di uno stumento conosciuto come il compasso di Alfonso d'Iseo (1576-?) che Cavalieri definisce come una squadra zoppa.
I lati del compasso formano l'angolo di apertura del cono: uno dei due lati costituisce la generatrice fissa del cono, mentre l'altro lato,
al quale è fissato uno stilo, è mobile e può allungarsi o accorciarsi in modo che la punta resti sempre a contatto col piano di disegno.
Il piano sul quale viene tracciata la curva può essere diversamente inclinato rispetto al compasso; a seconda dell'inclinazione si ottiene una parabola,
un'iperbole o un'ellisse.
Il secondo metodo prevede l'utilizzo di un cono immaginario e come unico elemento reale lo stilo, corrispondente ad una generatrice del solido.
Contrariamente al caso precedente, il piano sul quale viene disegnata la curva è fisso e lo strumento deve essere "accomodato" rispetto ad esso.
A seconda dell'inclinazione del compasso si ottiene la sezione conica desiderata.
Il compasso utilizzato in questa seconda tipologia di costruzioni, dice di averlo "appreso li Molto RR.PP. Gesuiti, qual mi dicono essere
inventione, e fabrica del P. Scheiner dell'istessa Compagnia".
Le costruzioni che rientrano in questa categoria avvengono sul piano con l'utilizzo di diversi strumenti.
Cavalieri suddivide tali costruzioni in ulteriori due sottocategorie: costruzioni col filo e costruzioni con le righe.
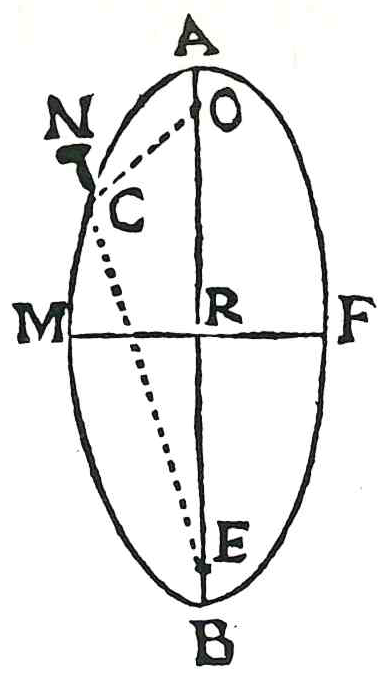
Costruzione dell'ellisse col filo
La costruzione dell'ellisse di asse maggiore \(AB\) e fuochi \(O\), \(E\), sfrutta la seconda proprietà della curva, cioè la proposizione 52 del terzo
libro delle Coniche di Apollonio (262-190 a.C.): \(OC + CE = AB\), dove \(AB\) equivale alla lunghezza del filo.
Data una corda di lunghezza \(AB\), si fissano gli estremi nei fuochi \(O\) ed \(E\).
Si posiziona lo stilo in \(N\) e, tenendo il filo teso, si traccia l'ellisse.
Cavalieri fa riferimento a questa costruzione come il metodo "più trito e noto" per tracciare la curva, metodo già noto agli antichi.
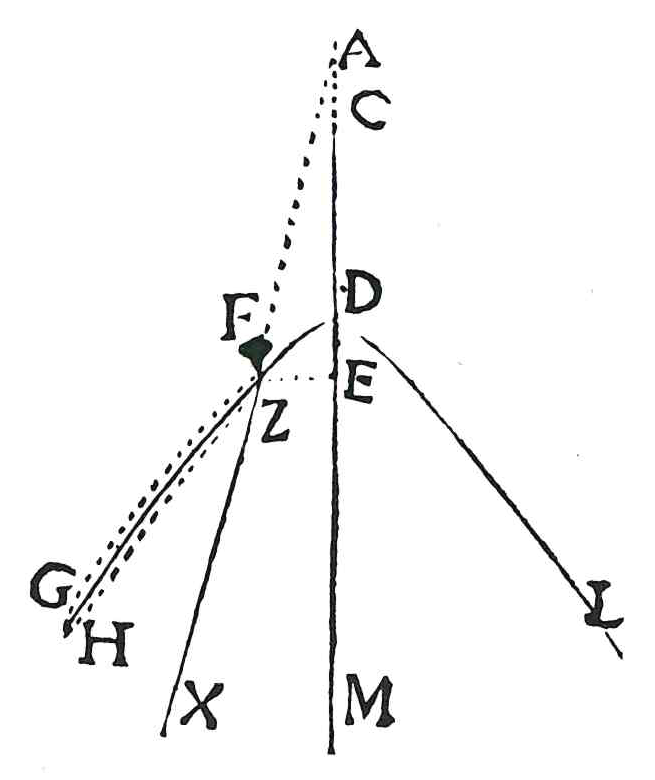
Costruzione dell'iperbole col filo
La costruzione dell'iperbole di fuochi \(A\), \(E\) e lato traverso \(CD\) avviene utilizzando una corda fissata in \(A\), \(G\), \(E\) che viene
fatta passare "doppia" attraverso uno stilo, posizionato in \(F\).
L'arco \(DH\) viene tracciato collocando lo stilo nel punto \(D\) e facendolo scorrere verso \(H\), tenendo il filo in tensione.
Si procede analogamente per l'arco \(DL\).
Per quest'ultima costruzione Cavalieri fa riferimento all'opera Ad Vitellionem paralipomena quibus astronomiae pars optica traditur di
Johannes Kepler (1571-1630), pubblicata nel 1604.
Il gesuato apporta però una modifica al metodo presentato dall'astronomo: utilizza uno stilo forato attraverso il quale possano passare e
scorrere i due rami della corda.
Il matematico completa le costruzioni col filo presentando quelle del compasso iperbolico e del compasso parabolico,
quest'ultima già proposta da Kepler.
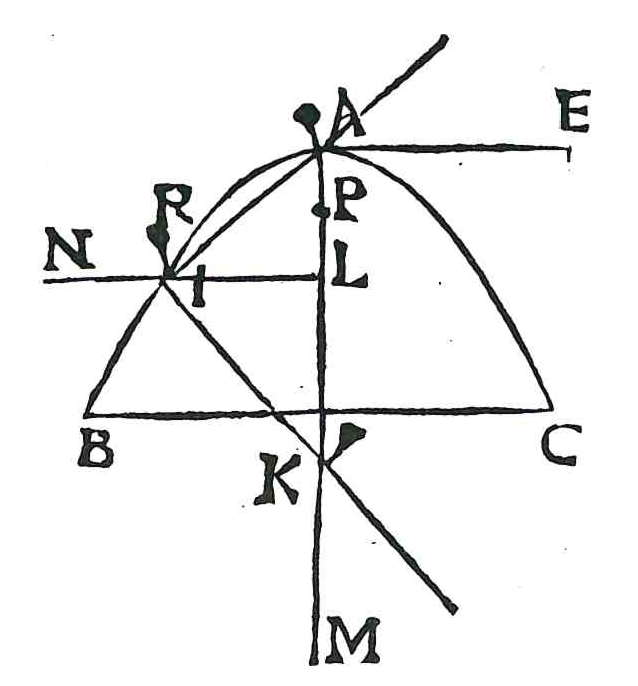
Costruzione della parabola con le righe
Per tracciare la parabola di asse \(AM\) e lato retto \(AE\) occorrono due squadre: \(AIK\) e \(NLM\).
Si fissano quindi due "pironcini" in \(A\) e \(K\), in modo tale che \(LK = AE\).
Lo stilo viene posizionato nell'angolo della squadra \(AIK\).
Per tracciare l'arco \(AB\) si posizionano inizialmente le squadre in modo tale che \(LK\) e \(IK\) siano disposti lungo il lato \(AM\) e i punti \(A\),
\(I\), \(L\) coincidano.
Facendo scivolare \(LK\) verso il basso lungo \(AM\) e la matita puntata in \(I\) lungo \(NL\), essendo presenti i due "pironcini" che fungono da perno,
viene tracciato il braccio \(AB\).
Analogamente si traccia il braccio \(AC\) della parabola.
Costruzione con Geogebra
Le costruzioni dell'iperbole e dell'ellisse avvengono tramite l'utilizzo di un dispositivo simile a quello appena descritto.
Lo Specchio Ustorio è forse il primo lavoro a stampa che proponga meccanismi di questo tipo per tutte e tre le coniche.
Le costruzioni delle coniche per punti continuati si ottengono tramite l'utilizzo di medie proporzionali.
Costruzione della semiparabola per punti continuati
Per costruire la semiparabola di asse \(AX\) e lato retto \(AZ\), si scelgono i punti \(H\), \(L\), \(M\), \(X\) sull'asse \(AX\).
Si conducono le rette \(HB\), \(LD\), \(MF\), \(XG\) e \(AV\) perpendicolari ad \(AX\).
Si tracciano i semicerchi \(ZCH\), \(ZOL\), \(ZIM\), \(ZVX\) e si individuano i punti d'intersezione con la retta \(AV\); infine si tracciano le
rette perpendicolari all'asse, tali che \(HB=AC\), \(LD=AO\), \(MF=AI\) e \(XG=AV\).
I punti \(A, B, D, F, G\) giacciono sulla semiparabola.
Costruzione con Geogebra
Tale costruzione era già stata descritta dal matematico tedesco Johannes Werner (1468-1522) nel Libellus super Vigintiduobus Elementis Conicis
pubblicato nel 1522.
Prosegue poi con due metodi simili per tracciare la semiellisse e l'iperbole.
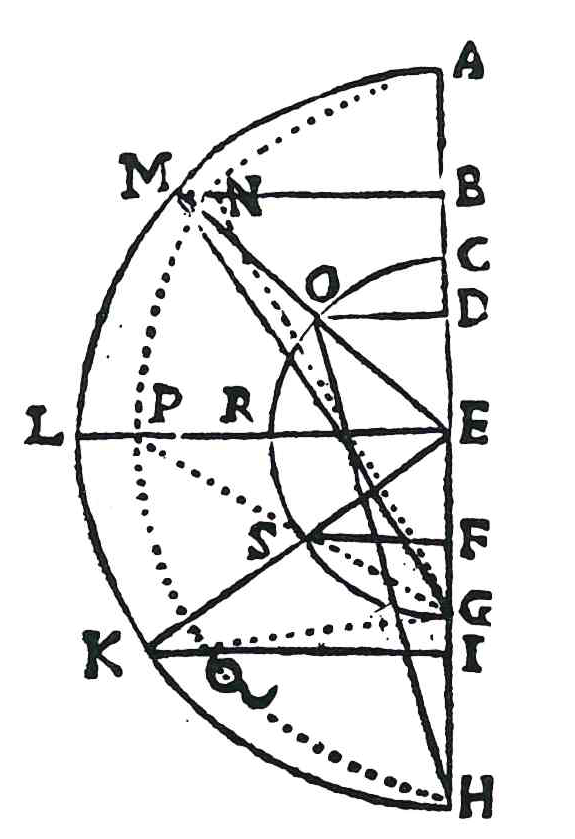
Costruzione dell'ellisse da due circonferenze per punti continuati
Per tracciare l'ellisse utilizzando due circonferenze, siano dati l'asse maggiore \(AH\) e la distanza focale \(CG\).
Viene individuato il punto medio \(E\) di \(AH\) e vengono tracciate due circonferenze di centro \(E\) e diametri \(AH\) e \(CG\).
Si prendono tre punti \(M\), \(L\), \(K\) sulla circonferenza maggiore e si tracciano i raggi \(ME\), \(LE\) e \(KE\).
Tali raggi intersecano la circonferenza minore in \(O\), \(R\), \(S\).
Dai sei punti sulle circonferenze si tracciano le perpendicolari all'asse \(AH\) individuando i punti di intersezione con quest'ultima: \(B\),
\(D\), \(E\), \(F\), \(I\).
Si descrive l'arco di circonferenza di raggio \(HD\) e centro \(G\), tale arco interseca \(MB\) in \(N\); si traccia poi l'arco di raggio \(HE\)
e centro \(G\) che interseca \(LE\) in \(P\) e l'arco di raggio \(HF\) e centro \(G\) che interseca \(KI\) in \(Q\).
I punti \(A\), \(N\), \(P\), \(Q\), \(H\) appartengono all'ellisse.
Costruzione con Geogebra
Tale costruzione era già stata presentata da Kepler nel trattato Tabulæ Rudolphinæ, pubblicato nel 1627.
L'astronomo la descrive in relazione al moto dei pianeti: il fuoco \(G\) rappresenta il Sole, \(A\) l'Afelio, \(H\) il perielio e la semiellisse
\(APH\) la semiorbita dei pianeti.
Costruzione della parabola da una circonferenza per punti continuati
Per costruire la parabola di asse \(AK\) e fuoco \(B\), si considera la circonferenza di raggio \(AC=2AB\) e centro \(C\) che interseca in \(F\) l'asse \(AK\).
Si traccia la perpendicolare all'asse \(AK\) in \(F\) e si riporta il segmento \(AF\) su tale retta, in modo tale che siano \(NF=FG=AF\).
Si considera un qualsiasi punto \(E\) interno ad \(AF\) e si traccia la perpendicolare ad \(AK\) in \(E\), individuando i punti di intersezione \(O\) e \(Z\)
con la circonferenza.
Si riporta sulla perpendicolare in \(E\) il segmento \(AO\), in modo tale che risultino \(ME=EH=AO\).
I punti \(N\), \(M\), \(A\), \(H\), \(G\) appartengono alla parabola.
Costruzione con Geogebra
Costruzione dell'iperbole equilatera e infinite iperboli per punti continuati
Lo stesso metodo appena esposto, se applicato alla parabola \(DQH\) generata dalla circonferenza di raggio \(DF\) e centro \(F\), dà luogo all'iperbole
equilatera \(DRI\).
Si tratta di tracciare la circonferenza di raggio \(DQ\) e centro \(F\), per identificare il punto d'intersezione \(R\) con la perperdicolare a \(DG\) in \(E\).
Infine si traccia la circonferenza di raggio \(DH\) e centro \(G\), per identificare il punto di intersezione \(I\) con la perperdicolare a \(DG\) in \(G\).
I punti \(D, R, I\) giacciono sull'iperbole equilatera.
Applicando nuovamente il metodo all'iperbole equilatera \(DRI\) si otterriene la parabola \(DSM\), e quindi infinite iperboli.
Costruzione con Geogebra
Gli ultimi due metodi esposti da Cavalieri sono stati "per qualche tempo stimati come cosa" di sua "inventione particolare".
Successivamente ammette di avere visto delle costruzioni simili nell'opera Curvi ac recti proportio del matematico svizzero Bartolomeo Sovero
(1576-1629), pubblicata nel 1630.
I metodi del Sovero sono descritti più dettagliatamente e alcune affermazioni che fa il Cavalieri in merito a tali costruzioni vengono dimostrate dal Sovero.
Lo svizzero inoltre propone un metodo più generale di quello presentato dal Cavalieri, riuscendo a unire più costruzioni in un'unica più generale.




![]()
![]()
![]()