| Agnesi Maria Gaetana |  |
Maria Gaetana Agnesi nacque il 16 maggio 1718 a Milano da Pietro, professore di matematica all'università di Bologna. Posta sotto la guida di ottimi insegnanti, abituali frequentatori della sua casa, ancora bambina, il 18 agosto 1727, recitò nel salotto paterno una sua traduzione di un discorso dell'abate Gemelli sugli studi delle donne, l'Oratio qua ostenditur artium liberalium studia a femineo sexu neutiquam abhorrere (Orazione in cui si mostra che in nessun modo gli studi delle arti liberali sono detestati dal sesso femminile) (edita a Milano nel 1727 e a Padova nel 1729). Nel 1739, Maria Gaetana Agnesi intraprese lo studio assiduo delle matematiche, basandosi sul Traité analitique des sections coniques del marchese de l'Hôpital (1661-1704). L'incontro col padre olivetano Ramiro Rampinelli, avvenuto nel 1740, spinse l'Agnesi ad ampliare le sue ricerche algebriche. Nel 1748 all'Agnesi venne offerta l'aggregazione all'Accademia delle Scienze di Bologna. Nel 1750 sostituì il padre nell'insegnamento della matematica all'Università di Bologna. Nel 1752, alla morte del padre, al quale Maria Gaetana non avrebbe mai disubbidito, Benedetto XIV le offrì di ricoprire ufficialmente la cattedra, ma Agnesi rifiutò, ritirandosi completamente dalla vita pubblica per dedicarsi a opere di carità , come la cura dei poveri e dei malati, agli studi privati, compreso quello delle Sacre Scritture, e all'istruzione dei fratelli, delle sorelle e dei domestici di casa. Maria Gaetana rese casa Agnesi un rifugio per inferme ed ella stessa divenne serva e infermiera: aprì un piccolo ospedale, andò a vivere con le malate e, per far fronte alle spese, dopo aver venduto tutti i suoi averi, si rivolse ai conoscenti, alle autorità , alle opere pie. Finalmente, grazie a una donazione del principe don Antonio Tolomeo Trivulzi, nel 1771 fu istituito a Milano il Pio Albergo Trivulzio e il cardinale Giuseppe Pozzobonelli invitò Agnesi a ricoprire la carica di "visitatrice e direttrice delle donne, specialmente inferme". Nel 1783 si trasferì al Pio Albergo in qualità di direttrice, ma non abbandonò gli studi religiosi: tenne lezioni pubbliche di catechismo. Pur senza titoli accademici, era ormai una teologa e il cardinale Pozzobonelli, per decidere sull'ortodossia di uno scritto su politica e religione, si rivolse a lei. Continuò a lavorare al Trivulzio per ventisei anni fino alla morte, il 9 gennaio 1799. |
| Berkeley George |  o o |
George Berkeley nacque il 12 marzo 1685 a Kilkenny in Irlanda ed entra nella Duke of Ormonde's School a luglio del 1696, dove studiò fino a gennaio del 1700. Nonostante non avesse ancora 15 anni, si iscrisse al Trinity College a Dublino, pagando di tasca propria gli studi; ricevette una borsa di studio nel 1702, a seguito di una mostra. Ottenne la laurea breve nella primavera del 1704, completando il master nel 1707. È noto che, dopo la laurea, Berkeley preparò un manuale in cui esplorò le basi della notazione aritmetica e i principali processi aritmetici come funzioni di questa notazione, spiegandole senza ricorrere a tecniche algebriche o geometriche. Ciò venne pubblicato in Arithmetica nel 1707, con un'ulteriore raccolta di studi intitolata Miscellanea mathematica e Berkeley indicò questa matematica come il suo interesse primario per tre anni. Nel 1706 Berkeley divenne Junior Fellow del Trinity College a Dublino e, nello stesso anno, egli lesse il suo articolo Of infinites alla Dublin Philosophical Society, ma quest'opera venne pubblicata solamente dopo la sua morte. Berkeley, oltre ad aver svolto compiti di tutoraggio, studiò teologia e fu ordinato diacono nel febbraio del 1709 e sacerdote nell'anno successivo. Durante questo periodo, Berkeley pubblicò An Essay towards a New Theory of Vision (1709) e A Treatise concerning the Principles of Human Knowledge (1710); la prima opera indaga la percezione visiva degli oggetti, dunque una parte della teoria dell'ottica, mentre la seconda è un trattato puramente filosofico sulla natura delle idee e della conoscenza. Sebbene Berkeley continuò la sua collaborazione al Trinity College fino al 1724, egli trascorse la maggior parte del periodo tra il 1713 e il 1724 lontano da Dublino. Durante il viaggio di ritorno per l'Inghilterra trascorse un po' di tempo a Lione dove scrisse il saggio De motu: Sive; de motu principio et natura, et de causa communicationis motuum (chiamato brevemente De motu, ossia Sul moto) che candidò per il Grand Prix of the Academy of Sciences, ma non ebbe successo. Raggiunse Londra nel 1721 e all'inizio dell'anno accademico 1721-22 egli era a Dublino con la nomina di Senior Fellow. Assunse incarichi aggiuntivi come: bibliotecario, preside, professore di lingua greca ed ebraica, di teologia e procuratore senior. Nel maggio del 1724 Berkeley si ritirò dal Trinity College per diventare decano anglicano di Londonderry. Egli, però, non risiedette mai in città , trascorrendo la maggior parte dei successivi quattro anni a Londra, durante i quali progettò di istituire un collegio alle Bermuda per formare i figli dei coloni e i selvaggi d'America; per tale progetto furono promessi a Berkeley fondi di 10000 sterline. Il primo di agosto del 1728 egli sposò Anne Foster e poco dopo partirono per l'America; raggiunsero Newport, Rhode Island, dove comprarono una fattoria e, successivamente, nacquero i loro primogeniti. Berkeley attese inutilmente la quota prestabilita per poter costruire il collegio: a metà del 1731 divenne ovvio che non avrebbe mai ricevuto la sovvenzione e tornò a Londra in ottobre. Berkeley pensò che il fallimento del suo progetto alle Bermuda potesse essere dovuto alla resistenza dei liberi pensatori, la sua avversità nei loro confronti crebbe. La delusione di Berkeley a Newport diventò l'occasione immediata per scrivere le sue grandi opere rivolte ai "free thinkers": Alciphron: or The Minute Philosopher e The Analyst: or a discourse addressed to an infidel mathematician. Nel gennaio del 1734, Berkeley fu nominato vescovo di Cloyne e fu ordinato nella chiesa di St. Paul, a Dublino, il 19 maggio 1734. Ricoprendo questo incarico, si dedicò alla difficile situazione sociale ed economica dell'Irlanda, facendo del suo meglio come vescovo anglicano per aiutare tutti gli abitanti del paese. Berkeley è conosciuto nel mondo della matematica per The Analyst (1734), cioè un attacco alle basi logiche del calcolo infinitesimale sviluppato da Newton. Morì il 14 gennaio 1753 e fu sepolto nella Christ Church a Oxford il 20 gennaio. |
| Bolzano Bernard |  |
Bernard Bolzano nacque il 5 ottobre 1781 a Praga da Bernard Pompeius Bolzano e Maria Cecilia Maurer. Leducazione di Bolzano fu molto influenzata dallimpegno nel sociale del padre e dalla frequentazione del Ginnasio presso lordine religioso degli Scolopi (o Piaristi) avvenuta dal 1791 al 1796. È importante sottolineare che Bernard dalla formazione presso gli Scolopi portò con sé principalmente i doveri morali e in misura minore le credenze puramente religiose. Bolzano entrò nel 1796 alla Facoltà di Filosofia dellUniversità Carolina di Praga dove studiò filosofia, matematica e fisica. Egli fu particolarmente influenzato negli studi matematici dal Mathematische Anfangsgründe (Fondamenti matematici) di Abraham Gotthelf Kaestner, che si occupava di questioni filosofiche in matematica e si proponeva di dimostrare molti risultati ritenuti "ovvi" da altri matematici dellepoca. Nellannata 1799-1800 Bolzano si dedicò alla ricerca in matematica insieme a Frantiek Josef Gerstner e nellautunno del 1800, nonostante il parere contrario del padre, iniziò tre anni di studi teologici allUniversità Carolina. Portando avanti gli studi teologici preparò una tesi di dottorato sulla geometria e nel 1804 conseguì il dottorato con una tesi che esponeva il suo punto di vista sulla matematica e ciò che costituisce una prova matematica corretta. Due giorni dopo aver conseguito il dottorato, Bolzano fu ordinato sacerdote della Chiesa Cattolica di Roma. Bolzano si rese ben presto conto che non era il servizio sacerdotale la sua vocazione, bensì linsegnamento, infatti gli anni di studio della Teologia non avevano per nulla rafforzato le sue credenze religiose. Tuttavia Bolzano si convinse, grazie alle parole di un suo docente dellUniversità, che la fiducia in una dottrina era giustificata se avesse portato al bene morale. Per comprendere adeguatamente gli eventi della vita di Bolzano, è necessario descrivere la situazione della Boemia dellepoca. Dall'inizio del 17° secolo, dopo che le forze della Chiesa Cattolica di Roma sconfissero i protestanti boemi, la Boemia venne governata dagli Asburgo e annessa allImpero Austriaco. Di conseguenza il tedesco divenne la lingua di insegnamento nelle scuole di grammatica e all'Università Carolina e il nazionalismo ceco fu soppresso. Nel 1781 lImperatore del Sacro Romano Impero Giuseppe II concesse la tolleranza religiosa nel proprio regno ma lavvento della Rivoluzione francese che incoraggiava il libero pensiero destò timore nei governanti. Dunque per tenere insieme l'Impero, i sovrani decisero di muoversi contro tutte le organizzazioni nazionalistiche che avrebbero potuto incoraggiare idee di indipendenza nelle varie parti dellImpero. Nel 1804, l'Imperatore Francesco II, che regnava da Vienna, decise che un modo per contenere gli effetti dell'Illuminismo era rafforzare la presa della Chiesa Cattolica di Roma, tendenzialmente conservatrice e contraria al pensiero liberale e a questo fine istituì cattedre di filosofia della religione nelle Università dellImpero. Le cattedre dellUniversità venivano assegnate in seguito a dei concorsi; Bolzano partecipò a due di queste competizioni per ottenere la cattedra allUniversità Carolina. Un concorso era relativo alla cattedra di Matematica che era divenuto vacante alla morte di Stanisław Vydra, l'altro alla nuova cattedra di filosofia della religione istituita dallImperatore Francesco. Bolzano ottenne il massimo in entrambe le competizioni, ma l'Università preferì affidargli la cattedra di Filosofia della religione poiché quella di Matematica venne affidata a Ladislaw Jandera che aveva sostituito Vydra durante la sua malattia tra il 1801 e il 1804. Bolzano era sicuramente la persona sbagliata a ricoprire questo incarico, poiché credeva nella giustizia sociale, nel pacifismo e nell'uguaglianza per i boemi di lingua ceca, tutti ideali che lImperatore Francesco sperava e cercava di sopprimere. La sua nomina alla cattedra doveva essere confermata a Vienna ma ben presto si capì che Bolzano non era il conservatore cattolico che si sperava fosse. Bolzano combatteva contro ogni discriminazione, principalmente dei boemi di lingua tedesca nei confronti dei boemi di lingua ceca, e criticava anche l'antisemitismo mostrato dai boemi sia tedeschi che cechi. Nel 1815 Bolzano fu ammesso alla Royal Bohemian Society of Sciences, società bilingue che attingeva i suoi membri principalmente da boemi di lingua tedesca ma anche di lingua ceca. Inoltre pubblicò lopera On the Condition of the Two Nationalities in Bohemia nel 1816, in cui esponeva le proprie preoccupazioni sul fatto che i boemi cechi fossero dominati dai boemi di lingua tedesca. La carriera di Bolzano continuò e, nonostante fossero state presentate accuse contro di lui alla corte di Vienna nel 1816, nel 1818 fu eletto Decano della Facoltà di Filosofia dellUniversità Carolina. Bolzano fu sospeso dalla sua posizione nel dicembre 1819 dopo le pressioni del governo austriaco. Oltre a questo, venne messo agli arresti domiciliari, gli fu censurata la posta e gli fu impedito di pubblicare. Tra il 1821 e il 1825 fu processato dalla Chiesa e, nonostante lenergica difesa delle proprie opinioni, gli fu richiesto di ritrattare le sue presunte eresie. Bolzano si rifiutò di farlo e rassegnò le dimissioni. Dal 1823 trascorse le estati vicino al villaggio di Techobuz nella Boemia meridionale, nella tenuta dei suoi amici Josef e Anna Hoffmann, mentre trascorse gli inverni a Praga con il fratello Johann. Tra il 1830 e il 1841 visse esclusivamente con gli Hoffmann e quando Anna si ammalò nel 1841, Bolzano e i coniugi Hoffmann si trasferirono a Praga da Johann. Fu loccasione per Bolzano di tornare a far parte della Royal Bohemian Society of Sciences di cui fu presidente nel 1842-43. Nell'inverno del 1848 contrasse un raffreddore che, date le pessime condizioni dei suoi polmoni, lo portò alla morte. |
| Borel Emile |  |
Félix Edouard Justin Emile Borel nacque a Saint-Affrique il 7 Gennaio 1871. Il padre era un ministro protestante ed educò il figlio per i primi anni di vita, mentre la madre era figlia di un ricco mercante di lana. Quando Emile aveva undici anni lasciò casa e andò a vivere con la sorella maggiore a Montauben, dove frequentò il Liceo. Lì mostrò straordinari talenti e, diversi anni dopo, andò a Parigi come economo del Collége Sainte-Barbe. Mentre vi studiava, frequentò i corsi al Lycée Louis-le-Grand per prepararsi a sostenere gli esami per entrare allEcole Polytechnique e allEcole Normale. Ottenne il primo posto in entrambi questi esami e poté scegliere una delle due scuole. Borel era però fortemente convinto di desiderare un lavoro nella scienza, in particolare in matematica, ed era sicuro che le migliori opportunità per una tale posizione sarebbero state raggiunte studiando allEcole Normale. Aveva il sostegno di suo padre per la sua decisione, entrandovi nel 1889. Mentre studiava alluniversità, svolse un servizio militare con gli ingegneri a Montpellier. Pubblicò i suoi primi due documenti matematici nel 1890. Si trattava di lavori abbastanza minori ma comunque notevoli per un giovane studente universitario che aveva appena iniziato i suoi studi. Nel 1892 gli fu assegnata la agrégation in matematica e nello stesso anno fu pubblicato il suo sesto lavoro, ovvero la sua prima grande opera. Un anno dopo gli fu conferito il dottorato. Nello stesso periodo, quando aveva solo 22 anni, Borel fu nominato Maître de Conférence allUniversità di Lille: vi trascorse tre anni, durante i quali pubblicò 22 articoli, con molti altri nelle mani dello stampatore quando se ne andò. Ritornò a Parigi nel gennaio 1897 quando fu nominato Maître de Conférence allEcole Normale Supérieure. Borel ottenne molti risultati negli anni successivi, sia nella sua carriera, che nella straordinaria matematica che produsse. Dal 1899 al 1902 insegnò al Collége de France e fu riservato al Cours Peccot (corso di matematica di un semestre tenuto da un matematico di età inferiore ai trenta anni che si è distinto per il suo primo lavoro promettente. Il corso è costituito da una serie di lezioni frontali che consentono al vincitore di presentare le sue recenti ricerche). Fu nominato esaminatore per lingresso all Ecole Navale nel 1900, ricoprendo questa carica per dieci anni. Sempre nel 1905 fu eletto presidente della Società matematica francese. Nellottobre 1901 aveva sposato Marguerite Appell. Non ebbero figli, ma adottarono uno dei nipoti di Borel, Fernand Lebeau che fu successivamente ucciso durante la prima guerra mondiale. Nel 1909 Borel fu nominato a una cattedra di Teoria delle Funzioni creata appositamente per lui alla Sorbona e continuò a ricoprire questo incarico fino al 1941. Lanno 1910 lo vide raggiungere la prestigiosa carica di vicedirettore dellEcole Normale Supérieure. Durante la prima guerra mondiale si offrì volontario per il servizio militare e comandò una batteria di artiglieria. Tornare alla sua posizione allEcole Normale dopo la fine della guerra si rivelò emotivamente molto difficile per lui. Infatti si dimise da vicedirettore nel 1920 e questo periodo segnò un cambiamento di direzione sia nella sua carriera che nei suoi interessi di ricerca. Nel 1921 fu eletto allAcadémie des Sciences, diventando vicepresidente nel 1933 e presidente nel 1934. Sempre nel 1921 fu nominato successore di Joseph Boussinesq nella cattedra di Probabilità e Fisica matematica e, nellanno successivo, fondò lIstituto statistico delluniversità di Parigi. Nel 1928, con il sostegno finanziario di Rockefeller e Rothschild, fondò lIstituto Henri Poincaré e lo gestì per trentanni. Nel corso degli anni Borel pubblicò molte opere eccezionali e continuò anche durante la seconda guerra mondiale. Tuttavia fu anche coinvolto in combattimenti con la Resistenza e fu arrestato e imprigionato a Fresnes per un mese nel 1941, ma presto rilasciato. Morì a Parigi il 3 Gennaio 1956. |
| Carnot Lazare |  |
Lazare Nicolas Marguérite Carnot nacque il 13 maggio 1753 a Nolay in Borgogna in una famiglia borghese. Nel 1773 si laureò alla scuola militare di Mézières dove ebbe come docente di matematica e fisica Gaspard Monge. Nel 1783 diventò capitano e nel 1784 fu promosso al rango di generale. Dal 1787 divenne membro dell'Accademia di Scienze di Digione. Nel 1791 fu eletto all'Assemblea legislativa e nel 1792 alla Convenzione nazionale, assemblea esecutiva e legislativa in vigore durante lepoca della Rivoluzione francese. Nel 1794, sotto la direzione di Carnot e Monge, fu istituita una "grande école" chiamata École centrale des travaux publics ma l'anno successivo il suo nome fu cambiato in École Polytechni-que. Il 30 ottobre 1796 Carnot venne eletto Presidente del Direttorio. Nel 1797 la situazione politica in Francia divenne tale da non permettere a Carnot di rimanervi, infatti in seguito al colpo di Stato del 18 fruttidoro venne destituito dalla presidenza del Diret-torio e fuggì dapprima in Svizzera e poi a Norimberga in Germania. L'anno seguente Carnot tornò in Francia. Con Napoleone Primo Console, Carnot fu nominato ministro della guerra per un periodo di cinque mesi ma fu costretto a dimettersi a causa di una divergenza di opinioni con Bonaparte. Nel 1802 divenne membro del Tribunato e per fedeltà agli ideali repubblicani si oppose allo svi-luppo autoritario del regime consolare e al tentativo di nominare Napoleone Primo Console a vita. Continuò, tuttavia, a far parte del Tribunato fino a quando l'assemblea fu soppressa nel 1807, anno nel quale si ritirò dalla vita pubblica. L'invasione alleata del 1814 lo costrinse a ritornare sulla scena, infatti Napoleone lo nominò governatore della città di Anversa, dove rimase fino alla caduta dellImpero. Durante i Cento giorni Napoleone, tornato dallesilio allisola dElba, nominò Carnot Ministro degli Interni. Dopo la sconfitta di Napoleone a Waterloo, Carnot lo incoraggiò a resistere, ma invano; e così la Seconda Restaurazione segnò la fine della carriera politica di Carnot. Nel luglio 1815 Carnot fu esiliato dalla Francia e si stabilì a Varsavia nel gennaio 1816. Nell'ago-sto 1816 Carnot lasciò Varsavia per Magdeburgo. Lazare Carnot morì il 2 Agosto 1823 a Magdeburgo. Solo nel 1889 la salma venne rimpatriata e inumata a Parigi nel Panthéon. |
| Cauchy Augustin Louis |  |
Augustin Louis Cauchy nacque a Parigi, il 21 agosto 1789, allalba della
Rivoluzione Francese. Il padre di Cauchy ebbe un ruolo attivo
nellistruzione del figlio, che ebbe anche le eccezionali influenze di
Laplace e, soprattutto, Lagrange. Proprio dietro suo suggerimento,
Cauchy entrò allÉcole Centrale du Panthéon
nel 1802 per studiare latino e greco, fondamentali per costruire delle
solide basi matematiche. Due anni dopo Cauchy cominciò a frequentare
corsi di matematica e nel 1805 entrò allÉcole Polytechnique dove il suo
mentore di analisi fu Ampère. Si diplomò nel 1807 come uno degli
studenti migliori. I suoi sforzi nella matematica non erano solo quelli
di studente: nel 1811 pubblicò il suo primo articolo sui poliedri, dove
dimostrava che gli angoli di un poliedro convesso sono determinati dalle
sue facce. Tra il 1813 e il 1814 si concentrò progressivamente sulla ricerca, pubblicando ad esempio una importante memoria sugli integrali definiti che costituirà in seguito la base per la sua teoria delle funzioni complesse. Nonostante ciò, non riuscì ad ottenere nessuna delle cattedre per cui fece domanda: in parte ciò fu dovuto alle sue profonde convinzioni religiose - era un devoto cattolico e il suo atteggiamento lo portò spesso a ritrovarsi isolato dai suoi pari. Nel 1815 venne finalmente assegnato al ruolo di professore associato di analisi allÉcole Polythecnique, dove sarebbe stato responsabile del corso del secondo anno. È linizio di un periodo positivo per Cauchy, che lanno successivo vinse il Grand Prix dellAccademia Francese delle Scienze per un lavoro sulle onde e raggiunse la vera fama dimostrando una delle affermazioni irrisolte di Fermat sui numeri poligonali. Inoltre un mutamento di establishment scalzò Carnot e Monge dal favore politico, permettendo a Cauchy di ottenere un posto allAccademia delle Scienze. Tra il 1817 e il 1830 sostituì Jean-Baptiste Biot al Collège de France e continuò a insegnare allÉcole Polythecnique. È in questi anni che compì i passi più significativi nel calcolo infinitesimale: nel 1821 pubblicò il Cours danalyse, un libro di testo scritto con lobiettivo di sviluppare le basi per i teoremi del calcolo nel modo più rigoroso possibile; nel 1823 il Calcul infinitésimal, dove compaiono per la prima volta le definizioni moderne del calcolo differo-integrale; infine nel 1826 cominciò a studiare il calcolo dei residui e tre anni dopo definì per la prima volta il concetto di funzione complessa di variabile complessa. Nel 1831 si trasferì a Torino, dove ricoprì la cattedra di fisica teorica dallanno successivo. È curioso come i corsi delluomo che aveva compiuto i più importanti passi avanti nella sistemazione rigorosa dellanalisi matematica fossero descritti dai suoi studenti come molto confusi, con balzi improvvisi da unidea allaltra, da una formula alla successiva, senza nessuna cura di fornire una connessione tra di loro. Le sue presentazioni erano nubi oscure, illuminate di quando in quando da lampi di puro genio. Significativa fu la sua successiva permanenza a Praga, dove nel 1834 incontrò Bolzano, il quale nel 1817 aveva pubblicato nel trattato Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey [sic] Werthen, die ein entgegengesetztes Resultat gewaehren, weningstens eine reele Wurzel der Gleichung liege una definizione di continuità praticamente identica a quella di Cauchy e che secondo alcuni storici potrebbe avere ispirato la definizione di Cauchy di continuità. Cauchy fece ritorno a Parigi nel 1838, dove riottenne la sua posizione alla Académie, ma il suo rifiuto di prestare giuramento di fedeltà al sovrano Luigi Filippo dOrleans gli negò la facoltà di insegnamento. Lanno successivo per lo stesso motivo, in aggiunta alla forte opposizione di Poisson, fu boicottato nella sua nuova mansione al Bureau des Longitudes. Le sue posizioni politiche e religiose (come il supporto per i Gesuiti) non cessarono di ostacolare la sua carriera neppure in seguito, quando nel 1843 gli venne preferito Libri matematico di capacità notevolmente inferiori come titolare della cattedra di matematica al Collège de France. Nei cinque anni successivi Cauchy si concentrò principalmente sulle equazioni differenziali e sulla matematica fisica pubblicando limportante opera in quattro volumi Exercices danalyse et de physique mathématique e studiando astronomia per la sua candidatura al Bureau des Longitudes. Nel 1848 Luigi Filippo dOrleans venne destituito dal trono e Cauchy riguadagnò la sua posizione universitaria, ma quando nel 1850 Libri rassegnò le sue dimissioni, Cauchy dovette scontrarsi con Liouville per la cattedra, come era accaduto peraltro proprio sette anni prima, quando il matematico italiano dimissionario aveva, a sorpresa, prevalso. Liouville vinse una combattuta elezione ma la successiva contesa per sovvertire la decisione del consiglio accademico seminò un duraturo astio tra i due. Unultima controversia adombrò gli ultimi anni di vita di Cauchy: Poncelet dimostrò di aver ottenuto un risultato sugli urti anelastici, con un lavoro del 1826, laddove Cauchy aveva affermato, sfidato poi da Duhamel, di essere stato il primo a scoprirlo, nel 1832. La sconfitta fu un duro colpo per lui: ... la disputa diede agli ultimi giorni della sua vita una tristezza radicata e unamarezza di cui solo i suoi amici erano a conoscenza... Morì il 23 maggio 1857 a Sceaux, non lontano da Parigi, alle quattro del mattino. |
| Fagnano Giulio Carlo |  |
Giulio Fagnano nasce a Senigallia il 6 dicembre 1682.
Insieme a suo padre Francesco e a suo madre Camilla Bartolini
appartiene a una della famiglie più in vista di Senigallia ai tempi
dello Stato Pontificio. Fagnano segue la vocazione familiare a prendere
parte alla vita pubblica della città e, pertanto, viene nominato
gonfaloniere nel 1723. Gonfaloniere significa letteralmente
"portabandiera" ed era un titolo di alti magistrati civici nelle
città -stato italiane medievali. Tali uffici non erano facili a quei
tempi e Fagnano viene sottoposto a molte false accuse mosse contro di
lui da cittadini invidiosi del suo status che stavano maliziosamente
cercando di danneggiare la sua reputazione. Fagnano mette al mondo
molti figli, fra i quali troviamo Giovanni che segue le orme del padre
interessandosi alla matematica. Giulio Fagnano studia matematica da
autodidatta e, sebbene fosse per lui una attività ricreativa, raggiunge
una notevole fama internazionale. Infatti ha suggerito nuovi metodi per
risolvere le equazioni di grado 2, 3 e 4 e ha migliorato il lavoro di
Bombelli su numeri complessi dando una famosa formula: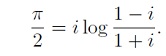 A lui si deve anche la scoperta che se G è il baricentro di un triangolo, allora 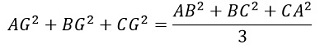 Fagnano introduce ingegnose trasformazioni analitiche che gettano le basi per la teoria degli integrali ellittici. Egli infatti studia gli archi di lemniscata, una curva di equazione 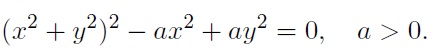 Per questa particolare curva nella nota Metodo per misurare la lemniscata, Schediasma II (1718) scrive una formula di duplicazione per la lunghezza degli archi di lemniscata che viene generalizzata da Eulero nella nota De integrazione aequazioni differenzialis 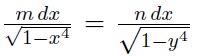 (1756) dove compare una formula di
addizione per gli archi di lemniscata. Le note di Fagnano vennero
pubblicate nel 1750 in un opera in due volumi dal titolo Produzioni
matematiche. (1756) dove compare una formula di
addizione per gli archi di lemniscata. Le note di Fagnano vennero
pubblicate nel 1750 in un opera in due volumi dal titolo Produzioni
matematiche. |
| Fatio de Duillier Nicolas |  |
Nicolas Fatio de Duillier è un matematico e astronomo svizzero. Amico di Huygens e Newton, ha sviluppato una teoria propria sulla gravitazione e una forma rudimentale di calcolo differenziale. Dopo aver preso parte alla disputa accusando Leibniz di plagio, nel 1706 entra a far parte di una setta religiosa. Da questo momento in poi, nonostante egli prosegua gli studi matematici, non viene più tenuto in considerazione né dai vecchi amici né dalla comunità scientifica. |
| Grandi Guido |  |
Guido Grandi nacque a Cremona il 10 Ottobre 1671 da Pietro Martire, ricamatore in oro, e Caterina Legati. Grandi studiò prima con il sacerdote camaldolese Pietro Canneti, poi nella scuola locale dei gesuiti. Vi studiò la retorica e nel 1687, studente di filosofia, vi conobbe il gesuita Girolamo Saccheri, che insegnava latino. A sedici anni, forse per l'esempio del Canneti e la tendenza agli studi, entrò nella congregazione dei Camaldolesi, assumendo il nome Guido in sostituzione degli originari Francesco Lodovico. A fine 1692 fu inviato a Roma, in S. Gregorio al Celio, per il corso di teologia. Proseguiti gli studi teologici a Roma e quelli geometrici e matematici a Firenze, nel 1700 divenne professore di filosofia nel monastero camaldolese di Firenze. Intanto, preparando i corsi di filosofia, conobbe i Principia Philosophiae cartesiani, che divennero struttura portante del suo insegnamento. Con la matematica pura coltivò le applicazioni: tra 1699 e 1700 mostrò buone conoscenze in ottica, meccanica, astronomia. Nel maggio del 1742 Grandi si aggravò e il 26 giugno fu colto da "deliquio" nella chiesa del monastero; morì il 4 luglio. Fu sepolto nella stessa chiesa, dove gli fu eretta un'edicola sepolcrale con un busto in marmo di G. Baratta e un'epigrafe del Forzoni. |
| Hôpital Guillaume |  |
Guillaume de l'Hôpital, Marchese di Sainte-Mesme, è nato a Parigi nel 1661 in una delle più illustri e rinomate famiglie francesi. Fin da bambino sviluppò da subito grandi abilità matematiche e dimostrò una forte passione per la materia. Tuttavia l'Hôpital seguì inizialmente la carriera militare che presto fu costretto a lasciare per la sua miopia. Da quel momento si dedicò totalmente alla matematica. Nel 1691 incontrò Johann Bernoulli, che giunto da Ginevra a Parigi, iniziò ad insegnare ai matematici della cerchia di Malebranche il nuovo calcolo infinitesimale di Leibniz. L'anno seguente il marchese si trasferì nella sua tenuta a Ouques e Bernoulli lo seguì per continuare ad impartirgli lezioni private sul calcolo. Quando nel novembre del 1692 Bernoulli lasciò Ouques e tornò a Basilea, il rapporto col marchese proseguì e i due stilarono un accordo in base al quale l'Hôpital avrebbe pagato annualmente a Bernoulli un compenso per continuare le lezioni sul calcolo. Tale accordo stabiliva però che Bernoulli non rivendicasse alcun diritto su tali risoluzioni e, ovviamente, che il patto rimanesse segreto. Questa fu la proposta di l'Hôpital: Le darò con piacere una pensione di 300 sterline, che inizia dal 1 gennaio di quest'anno, e invierò 200 sterline per la prima parte dell'anno, per gli appunti che hai inviato e le darò altre 150 sterline per l'altra parte dell'anno e così via in futuro. Prometto di aumentare queste pensioni presto, perché riconosco che siano moderate e lo farò e non appena i miei affari saranno meno confusi... Non sono così irragionevole da pretendere da lei tutto il suo tempo, ma le chiedo che mi conceda di tanto in tanto alcune ore per lavorare su ciò che le ho chiesto e che così mi comunichi le sue scoperte, con la condizione di non informare altri. Le chiedo, per favore, di non mandare né a Varignon né ad altri copie di queste note inviate a me. Mi invii la sua risposta a tutto questo e mi creda. Nel 1696, l'Hôpital pubblicò il manuale Analyse des infiniment petits pour l'intelligence des lignes courbes, che fu il primo testo di calcolo infinitesimale della storia e rappresentò una degli strumenti principali per la diffusione del calcolo a Parigi e in Europa. Negli anni successivi alla prima pubblicazione e in particolare dopo la morte del marchese, la proprietà intellettuale del manuale fu molto dibattuta: gran parte dei contenuti sembravano essere dovuti a Bernoulli, che si lamentò di non aver ricevuto sufficiente riconoscimento e di essere stato plagiato. Quando Johann Bernoulli ricevette una copia dell'Analyse, si lamentò con profonda amarezza e disperazione, in alcune lettere private indirizzate ad amici, che il marchese nel suo libro aveva plagiato palesemente parte dei suoi risultati. Poichè fu chiaro da subito che il patto proposto da l'Hôpital sarebbe andato a privare Bernoulli della paternità dei propri risultati matematici, ci si chiede il motivo per cui egli accettò così rapidamente la proposta del marchese, senza mai sottrarsene. Sebbene, come suggerisce Truesdell, il denaro possa aver giocato un ruolo importante, potrebbe non essere la sola ragione. Certamente lo status sociale era molto più importante in quest'epoca che nel mondo moderno e Bernoulli probabilmente si sentì, in larga misura, obbligato ad essere sottomesso ad un nobile. Ma è anche possibile che per il giovane Bernoulli fosse più importante che il calcolo leibniziano e le sue scoperte matematiche diventassero ben note, rispetto al fatto che il mondo sapesse che lui ne era l'autore. Solamente alla morte del marchese, nel 1704, Bernoulli si sentì sciolto dal patto e decise di rivendicare la paternità della regola e dei risultati di cui era stato privato. A causa della sua reputazione non proprio immacolata non fu però creduto immediatamente. L'Hôpital morì a Parigi il 2 febbraio 1704, all'età di 43 anni, e la sua memoria di matematico è sopravvissuta fino ai giorni nostri nel nome della celebre regola di l'Hôpital. Alla sua morte, lasciò il manoscritto completo di un secondo libro, Traité analytique des sections coniques et de leur usage pour la résolution des équations dans les problèmes tant déterminés qu'indéterminés, che fu poi pubblicato nel 1707. Si tratta di un trattato che si compone di definizioni, corollari, proposizioni e figure di riferimento e si concentra per lo più su costruzioni geometriche su coniche. Non ebbe lo stesso spirito e lo stesso significato dell'Analyse, e perciò nemmeno il suo medesimo successo. |
| Jordan Camille |  |
Camille Jordan nacque a Lione il 5 gennaio 1838. Il padre era un ingegnere educato all'Ecole Polytechnique, mentre la madre era la sorella del famoso pittore Pierre Puvis de Chavannes. Jordan studiò al Liceo di Lione e al Collége d'Oullins. Entrò all'Ecole Polytechnique per studiare matematica nel 1855. Questa scuola gli fornì la formazione per essere un ingegnere e Jordan, come molti altri matematici francesi del suo tempo, si qualificò come tale e intraprese quella professione. Sposò Marie-Isabelle Munet, figlia del vicesindaco di Lione, nel 1862. Ebbero otto figli, due femmine e sei maschi. Dal 1873 fu esaminatore presso l'Ecole Polytechnique, dove divenne professore di Analisi il 25 novembre 1876. Fu anche professore al Collége de France dal 1883, sebbene fino al 1885 praticasse la professione di ingegnere. E' significativo, tuttavia, che abbia trovato più tempo per intraprendere ricerche quando era un ingegnere: infatti, la maggior parte dei suoi lavori originali risalgono a questo periodo. Jordan lavorò in ambiti differenti, contribuendo essenzialmente a ogni argomento matematico che era stato studiato fino a quel momento. La topologia ebbe un ruolo importante in alcune delle sue prime pubblicazioni che rappresentavano un approccio combinatorio alle simmetrie e nel 1866 introdusse importanti concetti topologici. Inoltre, sviluppò per primo un approccio sistematico alla teoria dei gruppi finiti. Per il suo lavoro a riguardo, svolto tra il 1860 e il 1870, gli fu assegnato il premio Poncelet dell'Académie des Sciences. Jordan è oggi meglio ricordato tra analisti e topologi per la sua dimostrazione che il complementare di una curva chiusa semplice in R2 divide il piano in due componenti connesse, ora chiamato teorema della curva di Jordan. Ha anche originato il concetto di funzioni di variazione limitata ed è noto soprattutto per la sua definizione della lunghezza di una curva. Tutti questi concetti compaiono nel suo Cours d'analyse de l'Ecole Polytechnique, pubblicato per la prima volta in tre volumi tra il 1882 e il 1887. La seconda edizione apparve nel 1893, mentre il teorema della curva di Jordan apparve nella terza edizione del testo tra il 1909 e il 1915. Fino al 1882, quando fu pubblicato il primo volume, Jordan tenne lezioni all'Ecole Polytechnique e il libro fu scritto come un testo per gli studenti. Nel 1885 Jordan divenne editore de Il Journal de Mathématiques Pure et Appliquées: un importante giornale matematico che ha svolto un ruolo molto significativo nello sviluppo della matematica nel corso del XIX secolo. Egli mantenne questo incarico per oltre 35 anni, fino alla sua morte. Tuttavia, nel 1912 Jordan si ritirò da tutti i suoi incarichi. Gli ultimi anni della sua vita furono tristi a causa della prima guerra mondiale. Tra il 1914 e il 1916 tre dei suoi sei figli furono uccisi in guerra. Tra gli onori assegnati a Jordan vi fu la sua elezione all'Académie des Sciences il 4 aprile 1881. Il 12 luglio 1890 divenne ufficiale della Legione d'Onore. Fu il presidente onorario del Congresso internazionale dei matematici a Strasburgo nel settembre 1920. Morì a Parigi il 22 gennaio 1922. |
| Keill John | John Keill è un matematico e fisico scozzese. Ha studiato presso l'università di Edimburgo sotto la guida di David Gregory. Non ha grandi meriti scientifici, infatti durante la sua vita si è occupato soprattutto di politica e amministrazione. à ricordato per il ruolo che ha avuto nella disputa di difensore abilissimo e instancabile di Newton. | |
| Lagrange Giuseppe Luigi |  |
Joseph Louis Lagrange nasce a Torino il 25 gennaio 1736. Il padre, Giuseppe Francesco Lodovico, è tesoriere dell'artiglieria e la madre, Teresa Grosso, è la figlia di un medico del vicino paese Cambiano. A 14 anni viene mandato all'Università di Torino per seguire gli studi giuridici ma segue anche le lezioni di geometria di Filippo Rivelli e di fisica di Giovanbattista Beccarica. Nel 1754 crede di aver appena ottenuto il suo primo risultato originale del quale informa lo stesso Giulio Carlo Fagnano e che pubblicherà successivamente col titolo Lettera di Luigi De La Grange Tournier Torinese all'Illustrissimo conte Giulio Carlo Fagnano. Tuttavia si accorge presto che questa scoperta era già presente nella corrispondenza fra Leibniz e Bernoulli pubblicata nel 1745 a Losanna. Sempre nel 1754 Lagrange inizia a studiare i Methodus inveniendi lineas curvas di Eulero (1744) e lo informa con una lettera datata 28 giugno 1754 di alcune sue osservazioni sui massimi e sui minimi che si incontrano nei fenomeni della natura. Inizia quindi una fitta corrispondenza durante la quale il giovane Lagrange comunica ad Eulero le sue scoperte di calcolo delle variazioni, fra cui la soluzione del problema della brachiostocrona, nonché i suoi studi sul principio di minima azione. Le lettere di Fagnano e Eulero vengono usate dal padre di Lagrange come credenziali per procuragli la nomina, con decreto del 26 settembre 1755, a Sostituto del Maestro di Matematica nelle Regie Scuole di Teorica di Artiglieria. Gli studi astronomici di Lagrange iniziano nel 1762 a seguito di un concorso a premi indetto dall'Accademia delle Scienze di Parigi che proponeva lo studio dei moti lunari. Egli scriverà la memoria Recherches sur la libration de la Lune dove usa per la prima volta il principio dei lavori virtuali che sarà fondamentale nella sua Mécanique Analytique (1788). Nel 1766 Lagrange lascia Torino per trasferirsi a Berlino presso la corte di Federico II per ricoprire la carica di Direttore della classe di matematica presso l'Accademia delle Scienze. Nel 1767 prende in moglie Vittoria Conti, una sua cugina, che muore nel 1783 lasciandolo senza figli e in un evidente stato depressivo. Nello stesso anno muoiono anche Eulero e d'Alembert ma i problemi giungono nel 1786 quando muore Federico secondo. Lagrange si vede costretto a trasferirsi a Parigi accettando così l'offerta fattagli dal governo francese. Agli inizi del suo soggiorno parigino era sostanzialmente convinto che la matematica non era più suscettibile a sviluppi futuri. Pertanto si disinteressa alla ricerca matematica e attratto dalla chimica partecipa al circolo di Lavoisier. Nel 1790 entra nella Commissione pesi e misure nominata dall'Assemblea costituente e nel 1792 sposa la figlia dell'astronomo francese Pierre Charles Le Monnier, suo collega. Nel 1794 viene fondata l'Ecole Polytechnique di cui Lagrange ne è il primo professore di analisi e nel 1795 l'Ecole Normale che aveva come obiettivo la formazione di nuovi docenti e la standardizzazione dell'insegnamento. Lagrange insieme a Monge e Laplace terrà diverse lezioni che incisero sul rinnovamento della didattica della matematica. Muore a Parigi il 10 aprile 1813. |
| Lebesgue Henri |  |
Henri Léon Lebesgue nacque a Beauvais, in Francia, il 28 Giugno 1875. Il padre, tipografo, morì di tubercolosi quando suo figlio era ancora molto giovane, ed egli stesso soffrì durante tutta la sua vita a causa di una salute molto cagionevole. Lebesgue iniziò i suoi studi al Collége de Beauvais, dove mostrò di essere un brillante studente, poi si trasferì a Parigi, dove studi prima al Lycée Saint Louis e poi al Lycée Louis-le-Grand. Entrò allEcole Normale Supérieure nel 1894 e gli fu conferito il diploma di insegnante in matematica nel 1897. Per i successivi due anni, studiò nella sua biblioteca dove lesse gli articoli di Baire sulle funzioni discontinue e realizzò che si poteva ottenere molto di più in questo ambito. Più tardi ci sarà anche una notevole rivalità tra i due. Fu poi nominato professore al Lycée Centrale di Nancy dove insegnò dal 1899 al 1902. Basandosi sul lavoro di altri, tra cui quello di Emile Borel e Camille Jordan, Lebesgue formulò la teoria della misura nel 1901 e nel suo famoso articolo Sur une généralisation de lintégrale définie, apparso nel Comptes Rendus il 29 aprile 1901, diede la definizione di Integrale di Lebesgue, che generalizza la nozione dellintegrale di Riemann, estendendo il concetto dellarea sottintesa da una curva, includendo molte funzioni discontinue. Questa generalizzazione dellintegrale di Riemann ha rivoluzionato il calcolo integrale. Il contributo di Lebesgue è uno dei risultati dellanalisi moderna che amplia notevolmente la portata dellanalisi di Fourier. Questo eccezionale lavoro appare nella sua tesi di dottorato "Intégrale, longueur, aire", presentata alla Facoltà di Scienze di Parigi nel 1902 e pubblicata a Milano negli Annali di Matematica lo stesso anno. Lebesgue ottenne il suo primo incarico universitario quando nel 1902 divenne maître de conférences in matematica presso la Facoltà di Scienze di Rennes. Il 3 dicembre 1903 sposò Louise-Marguerite Vallet da cui ebbe due figli. Tuttavia, il matrimonio durò fino al 1916 quando divorziarono. Un onore che Lebesgue ricevette in una fase iniziale della sua carriera fu linvito a tenere il Cours Peccot al Collége de France. Lo fece nel 1903 e poi ricevette un invito anche due anni dopo, nel 1905. Egli discusse per la prima volta con Baire nel 1904, quando questultimo tenne il Cours Peccot al Collége de France, su chi avesse il diritto di insegnare in un tale corso. La loro rivalità si trasformò, più tardi, in una discussione più seria. Lebesgue scrisse due monografie: Leçons sur lintégration et la recherche des fonctions primitives (1904) e Leçons sur les séries trigonométriques (1906), che nacquero da questi due corsi di conferenze e servirono a far conoscere meglio le sue idee importanti. Tuttavia, il suo lavoro ricevette unaccoglienza ostile da parte degli analisti classici, soprattutto in Francia. Nel 1906 venne assunto dalla Facoltà di Scienze di Poitiers e lanno successivo vi fu nominato professore di meccanica. Fu nominato maître de conférences in Analisi Matematica alla Sorbona nel 1910. Durante la prima guerra mondiale lavorò per la difesa della Francia, e in quel periodo conobbe Emile Borel, che stava svolgendo un compito simile. Lebesgue rimase alla Sorbona fino al 1918, quando fu promosso Professore di Applicazioni di geometria allanalisi. Nel 1921 fu nominato professore di matematica al Collége de France, una posizione che mantenne fino alla sua morte. Insegnò anche allEcole Supérieure de Physique et de Chimie Industrielles de la Ville de Paris tra il 1927 e il 1937 e allEcole Normale Supérieure a Sévres. Ha anche dato importanti contributi in altre settori della matematica, tra cui topologia, teoria del potenziale, problema di Dirichlet, calcolo delle variazioni, teoria degli insiemi. Nel 1922 aveva scritto quasi 90 libri e articoli. Dopo il 1922 rimase attivo, ma i suoi contributi furono diretti verso questioni pedagogiche, lavori storici e geometria elementare. Morì a Parigi, il 26 Luglio 1941. |
| Leibniz Gottfried Wilhelm von |  |
Gottfried Leibniz nasce l'1 luglio 1646, da Friedrich, professore di filosofia, e Catharina Schmuck. Nel 1661, Leibniz entra all'Università di Lipsia. Studia, principalmente, filosofia e segue alcuni corsi sulla retorica e le lingue. Si laurea nel 1663 con la tesi Disputatio Metaphysica de Principio Individui (Metaphysical Disputation on the Principle of Individuation); successivamente Leibniz si reca a Jena per il periodo estivo. A Jena, il professore di matematica è Erhard Weigel; egli è anche un filosofo ed insegna a Leibniz l'importanza del metodo della dimostrazione matematica, applicato a materie come la logica e la filosofia. Egli ritiene che il numero sia un concetto fondamentale dell'universo e probabilmente le sue idee influenzano in modo considerevole Leibniz. Alla fine del 1663 Leibniz torna a Lipsia ed inizia gli studi per conseguire la laurea in legge. Conquista un Master in filosofia grazie ad una dissertazione, Specimen Quaestionum Philosophicarum ex Jure collectarum (An essay of Collected Philosophical Problems of Right), la quale combina gli aspetti della filosofia e della legge studiando le relazioni tra questi argomenti attraverso le idee matematiche imparate da Weigel. Nel 1665 si laurea in Legge, dopo un solo anno di studi, con la tesi De conditionibus (On Conditions). Nonostante la sua crescente reputazione scolastica, a Leibniz viene rifiutato il dottorato in legge a Lipsia, perciò si trasferisce immediatamente all'Università di Altdorf dove consegue il titolo agli inizi del 1667. Da novembre di quell'anno Leibniz vive a Francoforte; lavora come impiegato del Barone Johann Christian von Boyneburg, conosciuto quando era segretario in una società di chimici di Norimberga. In questi anni, Leibniz svolge le mansioni di segretario, assistente, bibliotecario, avvocato e consulente di Boyneburg. Leibniz si trasferisce a Parigi nel 1672, dove studia matematica e fisica sotto la guida di Christian Huygens; agli inizi del 1673, compie il primo viaggio a Londra, visita la Royal Society e mostra la sua, ancora incompleta, macchina calcolatrice. La Royal Society elegge Leibniz come membro il 19 aprile 1673. Nel 1675, a Parigi, Leibniz sviluppa le sue basi sul calcolo differenziale e le pubblica nove anni dopo. I dettagli sul suo calcolo differenziale compaiono in Nova methodus pro Maximis et Minimis, itemque Tangentibus (A new method for maxima and minima, and for tangents, that is not hindered by fractional or irrational quantities, and a singular kind of calculus for the above mentioned) negli Acta Eruditorum, un periodico creato a Lipsia due anni prima per informare sulle novità scientifiche e letterarie. Il trattato contiene la notazione a noi familiare, l'introduzione dei differenziali e le regole per lavorare con essi, cioè le regole per la derivazione. Newton scrive due lettere a Leibniz tramite Oldenburg, segretario della Royal Society, nel 1676. Le lettere contengono alcuni risultati ottenuti da Newton, come lo sviluppo e l'inversione delle serie. Newton non menziona il suo metodo delle flussioni e la soluzione delle equazioni differenziali in base a serie di potenze. In replica Leibniz esprime per la prima volta la sua notazione del calcolo e mostra, alquanto dettagliatamente, come trovare la pendenza della retta tangente a una curva algebrica. Leibniz accetta dal Duca di Hannover, Johann Friedrich, il posto di bibliotecario e consigliere di corte, a Hannover. Lascia Parigi nell'ottobre 1676 e si trasferisce ad Hannover, facendo tappa a Londra e in Olanda. Per il resto della sua vita, da dicembre 1676 fino alla morte, Leibniz rimane ad Hannover tranne che per alcuni viaggi. Nel 1686 pubblica, sempre sugli Acta Eruditorum, un articolo in cui si trova, per la prima volta, la notazione di integrale ∫.. La maggior parte dell'attività di Leibniz negli ultimi anni di vita, è incentrata sulla disputa con Newton per l'invenzione del calcolo. Nel 1711, legge osservazioni offensive sul suo conto scritte da Keill nella rivista Transactions of the Royal Society of London, dal quale è accusato di plagio. Leibniz chiede una ritrattazione, affermando di non aver mai sentito parlare di calcolo delle flussioni prima di aver letto l'Algebra di Wallis (1685) dove viene reso noto il lavoro di Newton sul teorema binomiale e il metodo delle flussioni. Leibniz scrive nuovamente alla Royal Society per richiedere una corretta procedura contro le accuse di Keill. In risposta alla sua lettera, la Royal Society istituisce una commissione, non del tutto imparziale, allo scopo di pronunciare il verdetto sulla disputa. Il verdetto della commissione, a favore di Newton, è scritto dallo stesso Newton e pubblicato col titolo Commercium Epistolicum (1713). Leibniz, in risposta al verdetto della Royal Society, pubblica in maniera anonima la Charta Volans. Leibniz muore ad Hannover il 14 novembre 1716. |
| Maclaurin Colin |  |
Colin Maclaurin nasce a Kilmodan in Scozia nel febbraio del 1698. Suo padre, John Maclaurin, è pastore della parrocchia locale ed è il terzo di tre fratelli. John è il maggiore e seguirà le orme del padre mentre Daniel, il fratello di mezzo, morirà in tenera età . Nel 1707, all'età di nove anni, Colin rimane orfano e con suo fratello viene preso in custodia dallo zio Daniel Maclaurin, pastore della chiesa di Kilfinan. Nel 1709 inizia gli studi presso l'Università di Glasgow che terminerà all'età di quattordici anni, conseguendo la laurea con una dissertazione che aveva come argomento On the power of gravity come argomento. Maclaurin indirizza la sua ricerca nell'ambito della geometria pubblicando nel 1720 uno studio sulle curve intitolato Geometrica Organica; Sive Descriptio Linearum Curvarum Universalis. Egli prende servizio all'Università di Edimburgo il 3 novembre 1725 dove acquista popolarità come insegnante anche se non riceve uno stipendio completo fino al 1742, quattro anni prima della sua morte. Nel 1742 Maclaurin pubblica il suo Treatise of fluxions, opera in due volumi che rappresentava la prima esposizione sistematica dei metodi di Newton. Nel 1745 ha un ruolo attivo nella difesa di Edimburgo durante l'insurrezione giacobita. Egli lavora intensamente nel tentativo di preparare le difese della città ma l'esercito giacobita raggiunge Edimburgo il 15 settembre 1745. Dopo il fallimento dei negoziati vengono aperte le porte della città ma il castello resiste. Muore il 14 giugno 1746 a Edimburgo e viene sepolto nella chiesa di Greyfriars dove la sua tomba è ancora visibile nell'angolo sud-ovest. |
| Manfredi Gabriele |  |
Gabriele Manfredi nacque a Bologna il 25 marzo 1681, figlio del notaio Alfonso e di Anna Maria Fiorini. Ben presto a causa di vicissitudini subite dal padre, la famiglia, composta da quattro figli maschi e due figlie femmine, si ritrovò in ristrettezze economiche, e, dopo aver abbandonato gli studi medici, si avvicinò, spinto anche da Domenico Guglielmini, agli studi matematici e riuscì a laurearsi nel dicembre 1702 in filosofia. Gabriele Manfredi ha vissuto la sua giovinezza in un ambiente ricco di stimoli. Il fratello Eustachio, di ingegno assai vivace, aveva fondato nel 1690 l'Accademia degli Inquieti, che fino al 1694 ebbe sede in casa dei fratelli Manfredi. Nelle sue riunioni venivano trattati i più svariati argomenti scientifici. Ad essa appartenevano anche Vittorio Francesco Stancari e Giuseppe Verzaglia, insieme ai quali Gabriele Manfredi incominciò, da autodidatta, lo studio dell'analisi leibniziana: mentre Stancari e Verzaglia si dedicavano all'applicazione del calcolo leibniziano a problemi di fisica matematica, Manfredi si interessava soprattutto della ricerca di regole generali in cui codificare il calcolo integrale. Dall'agosto 1708 Gabriele Manfredi cominciò a far parte della cancelleria senatoria bolognese e quest'impiego condizionerà pesantemente tutta la sua vita, e produrrà il rarefarsi della sua attività di ricerca in matematica. Nel 1720 ottenne la cattedra di Analisi e nel 1726 fu Cancelliere del Senato. Manfredi diventò nel 1742, dopo la morte del fratello Eustachio, sopraintendente delle acque di Bologna. Gli impieghi di cancelliere del senato e di sopraintendente delle acque del bolognese non hanno allontanato completamente Manfredi dalla ricerca matematica: forse è più esatto dire che a partire dal 1708 Manfredi non riuscì a dare un sistemazione definitiva ad alcuni studi che pur con difficoltà riusciva comunque a portare avanti. Manfredi morì il 13 ottobre 1761 e fu seppellito a Bologna nella chiesa di S. Maria Maddalena. |
| Newton Isaac |  |
Nasce a Wollsthorpe-by-Colsterworth, vicino Grantham nel Lincolshire nel 1642, da una famiglia contadina. Nel 1653 inizia a frequentare la Free Grammar School nel Grantham. I professori lo descrivono come inattivo e disattento, ma nonostante ciò prosegue gli studi grazie all'aiuto dello zio, William Ayscough, che lo prepara per entrare all'università . Newton viene ammesso al Trinity College di Cambridge nel 1661. Il suo obiettivo è una laurea in giurisprudenza, ma studia anche, la filosofia di Cartesio, Gassendi, Hobbes e in particolare Boyle. Inoltre lo entusiasmano l'astronomia di Copernico, la meccanica di Galileo e l'Optics di Keplero. Si pensa che il talento di Newton sia "spuntato" con l'arrivo di Barrow a Cambridge, come professore lucasiano nel 1663, in seguito incarico conferito a Newton nel 1669, e in effetti pochi anni dopo Barrow riconoscerà in lui il genio matematico. Nell'aprile del 1665 Newton si laurea a Cambridge; il suo talento scientifico non è ancora emerso, ma lo fa poco dopo quando è costretto a tornare nel Lincolshire a causa della peste che sta dilagando. Proprio in questo periodo, all'età di 25 anni, Newton compie le più grandi scoperte rivoluzionarie riguardo la matematica, l'ottica, la fisica e l'astronomia. Per quanto riguarda la matematica, getta le basi del calcolo differenziale e integrale, introducendo il "metodo delle flussioni", denominato così da lui. Oltre alle ricerche sul calcolo, Newton studia anche le serie, generalizza il teorema binomiale con esponenti non interi. Nel 1671 Newton scrive De Methodis Serierum et Fluxionum (Method of Fluxions), mai pubblicato fino alla traduzione in inglese nel 1736 di John Colson. Nel 1687 Newton pubblica Philosopiae naturalis principia matematica (Principles of Natural Philosophy), riconosciuto come il più grande libro mai stato scritto. Newton studia il moto dei corpi sotto l'azione di una forza centripeta. I risultati vengono applicati ai corpi in moto orbitale, ai proiettili, al pendolo e ai corpi in caduta libera vicino alla Terra. L'Università di Cambridge elegge Newton il 15 gennaio del 1689, come uno dei due membri universitari facenti parte del Parlamento. Dopo un crollo nervoso nel 1693, Newton si ritira dalla ricerca. Newton decide di lasciare Cambridge e si trasferisce a Londra per il posto di guardiano della Royal Mint, la zecca reale, nel 1696. Ottiene l'incarico grazie al patrocinato di Charles Montagu, primo Conte di Halifax e Cancelliere dello Scacchiere. Newton diviene successivamente Master della Royal Mint, dal 1699 e per i successivi trent'anni. Nel 1703 viene eletto presidente della Royal Society e membro dell'Académie des Sciences di Francia. Nominato cavaliere nel 1705 dalla regina Anne, è il primo scienziato a cui viene conferito questo titolo prestigioso. L'ultima parte della sua vita è dominata soprattutto dalla controversia con Leibniz sulla priorità dell'invenzione del calcolo differenziale. Newton sfrutta la sua posizione come presidente della Royal Society. La Royal Society nomina una commissione "imparziale" per giudicare la questione; Newton scrive il report ufficiale della commissione, senza far apparire il suo nome, che viene, poi, pubblicato nel Commercium Epistolicum nel 1713 e scrive anche una revisione, sempre anonima, pubblicata nel Philosophical Transactions of The Royal Society. Negli ultimi anni della sua vita, Newton si stabilisce a Cranbury Park, vicino Winchester con la nipote e suo marito e vi rimane fino alla sua morte avvenuta il 20 marzo 1727. Il suo corpo viene sepolto nell'Abbazia di Westminster. Newton lascia in eredità tutti i suoi beni alla famiglia. Dopo la sua morte, si esaminano i capelli di Newton e vengono rinvenute tracce di mercurio, probabilmente dovute agli esperimenti chimici eseguiti. |
| Oldenburg Henry |  |
Henry Oldenburg ha ricoperto la carica di segretario della Royal Society dal 1662 al 1677, sempre con l'obiettivo di mantenere i contatti tra gli scienziati di tutta Europa e di diffondere le scoperte inglesi. Nel 1665 ha fondato il primo periodico scientifico europeo, le Philosophical Transactions. |
| Peano Giuseppe |  |
Giuseppe Peano nacque il 27 agosto 1858 presso la frazione di Spinetta di Cuneo. Fu il secondogenito di Bartolomeo Peano e Rosa Cavallo. Dopo un inizio estremamente difficile, la famiglia si trasferì a Cuneo dove il fratello della madre, Giuseppe Michele Cavallo, accortosi delle notevoli capacità intellettive del nipote, lo invitò a raggiungerlo a Torino per continuare i suoi studi presso il Liceo classico Cavour. Si laureò poi in Matematica nell'Ateneo torinese nel 1880, divenendo subito assistente di Enrico D'Ovidio per il corso di Geometria e, dal 1881 al 1890, di Angelo Genocchi per il corso di Analisi, con cui nel 1884 scrisse il trattato "Calcolo differenziale e principi di calcolo integrale". Negli anni immediatamente successivi scrisse "Applicazioni geometriche del calcolo infinitesimale" (1887) e "Calcolo geometrico secondo l'Ausdehnungsehre di Grassman" (1988), con l'ambizione di costruire una geometria assoluta, capace di sostituire quella che ha bisogno del metodo delle coordinate. Peano utilizzò nei suoi studi il calcolo vettoriale, allora poco in uso. Proprio grazie a Peano e alla sua scuola questo tipo di calcolo si diffuse nell'ambiente matematico internazionale. Il 24 dicembre del 1885 aderì alla massoneria e dal 1886 al 1901 insegnò all'Accademia militare. Nel 1890 vinse la cattedra di Calcolo infinitesimale, rimasta vacante a causa della morte di Genocchi. Vittima della sua stessa eccentricità , che lo portava ad insegnare logica in un corso di calcolo infinitesimale, fu più volte allontanato dall'insegnamento a dispetto della sua fama internazionale. Peano è conosciuto, infatti, anche come pioniere nei campi della Logica e dei fondamenti della Matematica. Il progetto più ambizioso, cui dedicò tutte le sue energie a partire dal 1891, fu quello del Formulario, che voleva come l'opera più importante da lui compiuta: una grande enciclopedia matematica sotto forma simbolica completa, realizzata con l'aiuto di allievi e collaboratori. Terrà comunque il corso di calcolo infinitesimale fino al 1925, quando lo cederà a Francesco Tricomi, per impartire le lezioni di Matematiche complementari. Nel periodo dal 1908 al 1910, fu incaricato anche dell'insegnamento di Analisi superiore. Il corso gli verrà successivamente tolto per divergenze di opinioni con i colleghi. Morì il 20 aprile 1932, nella sua casa di campagna a Cavoretto, presso Torino, per un attacco di cuore che lo colse nella notte. |
| Riccati Jacopo |  |
Il conte Jacopo Francesco Riccati, nato a Venezia il 28 maggio 1676, è stato un matematico italiano, padre di Giordano Riccati e di Vincenzo Riccati, anch'essi matematici. Allievo di Stefano (degli) Angeli, Riccati si laureò a Padova nel 1696. Godette in vita di grande e meritata fama, ma rifiutò i molti incarichi onorifici offertigli, preferendo la vita familiare, che gli consentiva di dedicarsi meglio agli studi. Fu più volte consultato dal senato veneto, per la sua competenza in idraulica. La sua formazione matematica più moderna cominciò con la lettura dei Principia di Newton. Jacopo Riccati morì a Treviso, il 15 aprile 1754 senza aver raccolto gli inviti e recarsi presso Accademie estere che il suo prestigio scientifico europeo gli aveva procurato. |
| Riemann Bernhard |  |
Georg Friedrich Bernhard Riemann nacque il 17 Settembre 1826 a Breselenz, in Bassa Sassonia, figlio di Friedrich Bernhard Riemann, un pastore protestante luterano, e Charlotte Ebell. Friedrich Riemann si occupò personalmente dell'educazione dei suoi figli e in particolare fu precettore di Bernhard fino all'età di dieci anni. Successivamente Bernhard fu seguito da un insegnante locale di nome Schulz. Nel 1840 Bernhard entrò direttamente nella terza classe del Lyceum di Hannover. Negli anni di frequenza del Lyceum visse con la nonna ma, quando nel 1842 sua nonna morì, Bernhard dovette trasferirsi al Johanneum Gymnasium di Luneburgo. Nella primavera del 1846 Riemann si iscrisse alla facoltà di Teologia all'Università di Gottinga su insistenza del padre. Tuttavia frequentò alcune lezioni di matematica e se ne appassionò a tal punto da chiedere al padre il permesso di trasferirsi alla facoltà di filosofia in modo da poter studiare anche matematica. Ottenuto il permesso, Bernhard iniziò a frequentare i corsi tenuti da Moritz Stern e Carl Friedrich Gauss. Riemann si trasferì da Gottinga all'Università di Berlino nella primavera del 1847 per studiare con Jakob Steiner, Carl Jacobi, Peter Gustav Lejeun Dirichlet e Gotthold Eisenstein. La persona che principalmente influenzò Riemann in quel periodo fu Dirichlet. Fu durante il suo periodo all'Università di Berlino che Riemann elaborò la teoria generale delle variabili complesse che costituì la base di alcuni dei suoi lavori più importanti. Nel 1849 tornò a Gottinga dove nel 1851 fu presentata la sua tesi di dottorato sotto la supervisione di Gauss. Tuttavia non fu solo Gauss a influenzare fortemente Riemann in quel momento, infatti Wilhelm Weber aveva ottenuto una cattedra di fisica a Gottinga durante il periodo in cui Riemann era a Berlino, e Riemann fu il suo assistente per 18 mesi. Anche Johann Benedict Listing era stato nominato professore di fisica a Gottinga nel 1849. Attraverso Weber e Listing, Riemann acquisì una solida preparazione in fisica teorica e, in particolare grazie a Listing, maturò importanti idee in topologia che avrebbero influenzato la sua ricerca innovativa. La tesi di Riemann affrontava la teoria delle variabili complesse e, in particolare, le cosiddette superfici di Riemann; inoltre aveva introdotto metodi topologici nella teoria delle funzioni complesse. Per dimostrare alcuni dei risultati della sua tesi, Riemann utilizzò un principio variazionale che in seguito avrebbe chiamato "Principio di Dirichlet" perché lo aveva appreso durante le lezioni tenute da Dirichlet. La tesi di Riemann fu esaminata il 16 dicembre 1851. Su raccomandazione di Gauss, Riemann fu nominato a Gottinga e studiò per la sua abilitazione in modo da poter diventare poi professore. Lavorò trenta mesi alla sua tesi di abilitazione àber die Darstellbarkeit einer Funktion durch eine trigonometrische Reihe (Sullo sviluppo di una funzione in serie trigonometrica) che riguardava la rappresentabilità delle funzioni per serie trigonometriche. La cattedra di Gauss a Gottinga fu occupata da Dirichlet nel 1855 e in quell'occasione anche Riemann tentò di ottenere una posizione, ma invano. Due anni dopo, nel 1857, tuttavia, fu nominato professore. Nel 1859 Dirichlet morì e Riemann prese il suo posto alla cattedra di matematica a Gottinga il 30 luglio. Pochi giorni dopo fu eletto all'Accademia delle Scienze di Berlino, proposto dai matematici Kummer, Borchardt e Weierstrass. Nell'autunno del 1862 Riemann ebbe un forte raffreddore che si trasformò in tubercolosi. Riemann cercò di combattere la malattia trasferendosi nel clima più caldo d'Italia. Trascorse l'inverno del 1862-63 in Sicilia e poi viaggiò attraverso l'Italia, ritornò a Gottinga nel giugno 1863, ma le sue condizioni di salute presto si riaggravarono e dovette tornare di nuovo in Italia. Riemann visse dall'agosto 1864 all'ottobre 1865 nel nord Italia, poi tornò a Gottinga per l'inverno 1865-66 e poi nuovamente a Selasca sulle rive del Lago Maggiore il 16 giugno 1866. Morì il 20 settembre 1866 a Selasca e fu sepolto nel cimitero di Biganzolo di Verbania. |
| Taylor Brook |  |
Brook Taylor nacque il 18 agosto 1685 a Edmonton,
Middlesex, Inghilterra, da John Taylor e Olivia Tempest. La famiglia
era ai margini della nobiltà e il padre, che governava con rigorosa
disciplina, tramandò al figlio amore per musica e pittura. Entrò al St.
Johns College di Cambridge nel 1703 dove approfondì le sue conoscenze
matematiche, che in età più avanzata applicò alla musica e alla
pittura, laureandosi nel 1709.
Nel 1712 Taylor entrò a far parte della Royal Society grazie alle
raccomandazioni di John Machin e John Keill e due anni dopo fu eletto
segretario di questa società scientifica. Ricoprì questo incarico per
quattro anni, dimettendosi nel 1718 in parte per motivi di salute.
Questi quattro anni furono i più produttivi matematicamente. Tra il
1712 e il 1724 Taylor pubblicò tredici articoli su argomenti diversi,
tra cui la descrizione di esperimenti sull'azione capillare, il
magnetismo e i termometri. Pubblicò un resoconto di un esperimento per
scoprire la legge dell'attrazione magnetica (1715) e un metodo
migliorato per approssimare le radici di un'equazione introducendo un
nuovo metodo per calcolare i logaritmi (1717).
Due opere uscite nel 1715, Methodus incrementorum directa et
inversa e Linear Perspective sono
particolarmente importanti nella storia della matematica. Nella prima Methodus
incrementorum directa et inversa,
che ebbe una seconda
edizione nel 1717, Taylor aggiunse alla matematica un nuovo ramo ora
chiamato "calcolo delle differenze finite", inventò l'integrazione per
parti e scoprì, ma non fu il primo, la celebre "serie di Taylor",
serie
che sarà nota con questo nome solo più tardi. Il termine "serie
di
Taylor" sembra essere stato usato per la prima volta da Simon Antoine
Jean Lhuilier nel 1786. La prima menzione da parte di Taylor del
"Teorema di Taylor" apparve in una lettera che scrisse a John Machin
il
26 luglio 1712. Altri matematici, prima di Taylor, James Gregory,
Newton, Leibniz, Johann Bernoulli e de Moivre, indipendentemente tra
loro, avevano scoperto vari casi del teorema in questione. Gregory, per
esempio, ottenne lo sviluppo in serie della funzione arcotangente: 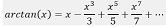 L'importanza del teorema di Taylor fu riconosciuta da Lagrange che nel 1772 lo pose alla base del calcolo differenziale. Vi sono altre idee importanti nel Methodus incrementorum directa et inversa che all'epoca non furono riconosciute come tali. Queste includevano soluzioni singolari delle equazioni differenziali, la regola di derivazione della funzione inversa e inoltre una discussione sulle corde vibranti, un interesse che quasi sicuramente proveniva dal primo amore di Taylor per la musica. L'altra opera uscita nel 1715, Linear Perspectives contiene i principi di base della prospettiva e la seconda edizione ebbe il titolo New Principles of Linear Perspective. Taylor si inserì nella disputa tra Newton e Leibniz sulla priorità del calcolo infinitesimale sfidando i "matematici non inglesi" a integrare un certo differenziale. Morì a Somerset House a Londra il 29 dicembre 1731. |
| Wallis John |  |
John Wallis è un matematico inglese che ha sviluppato metodi di interpolazione e valutazione di integrali. Ha insegnato geometria nell'università di Oxford per cinquant'anni ed era molto partecipe della vita politica anglosassone. Viene dipinto come xenofobo e conservatore, tanto che nei suoi scritti spesso attribuisce scoperte fatte da stranieri agli inglesi. Le sue opere più note sono Treatise of Angular Sections, Arithmetica infinitorum, Tract on Conic Sections e Treatise on Algebra. |