| 1.1 Leibniz e il calcolo infinitesimale (a cura di Giulia Bartolotti) |
| Leibniz è considerato uno degli inventori del calcolo
differenziale. Introduce diverse notazioni utilizzate ancora oggi, come
la esse allungata ∫ , iniziale della parola latina summa, per indicare
l’integrale, e la d, dalla parola latina differentia, per il
differenziale. La prima pubblicazione di Leibniz sul calcolo infinitesimale, Nova methodus pro Maximis et Minimis, itemque Tangentibus (A new method for maxima and minima, and for tangents, that is not hindered by fractional or irrational quantities, and a singular kind of calculus for the above mentioned), è contenuta nella rivista Acta Eruditorum del 1684. Il titolo dell’articolo può essere tradotto come “Nuovo metodo per i massimi e i minimi, come anche per le tangenti, che non si arresta davanti a quantità frazionarie e irrazionali, e modo unico di calcolo per i suddetti.” I metodi precedenti trovano il loro limite nella necessità di semplificare con artifici vari l’equazione 𝐹(𝐴)−𝐹(𝐴+𝐸)=0 prima di dividere per 𝐸 e poi porre 𝐸=0. La presenza di radici o di espressioni fratte complesse rende presto la strada non percorribile. Il punto cruciale sta nel fatto che la considerazione dell’equazione nella sua interezza non permette una separazione nelle varie parti più semplici che compongono l’equazione. In termini moderni si potrebbe dire che perché questa separazione divenga possibile è necessario scindere i due momenti del calcolo di 𝐹′ e della soluzione di 𝐹′=0, in altre parole si deve riconoscere il carattere di operazione sulle funzioni proprio della derivazione. Solo dopo questa constatazione è possibile operare prima il calcolo della derivata, mediante tutte le facilitazioni costituite dalla linearità e dalle regole di differenziazione di prodotti e quozienti, e poi utilizzarlo per la ricerca di massimi e minimi o per la determinazione delle tangenti. L’articolo inizia con la definizione di differenziale, inizialmente chiamato differenza: 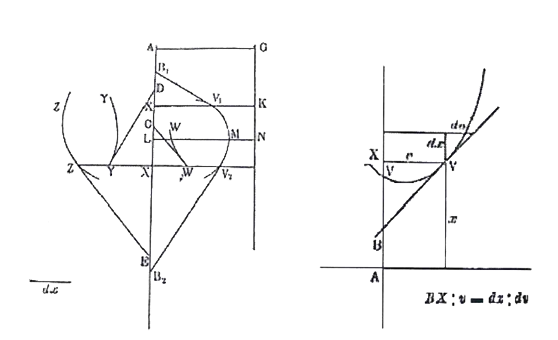 “Sia dato l’asse AX e più curve come VV, WW, YY, ZZ, e le ordinate di un loro punto, normali all’asse, siano VX, WX, YX, ZX: queste si dicano rispettivamente v,w,y,z; ed il segmento AX, tagliato sull’asse sia detto x. Le tangenti siano VB, WC, YD, ZE, le quali incontrano l’asse rispettivamente nei punti B, C, D, E. Ora un segmento preso ad arbitrio sia detto dx ed un segmento che sta a dx, come v (o w, o y, o z) sta a BX (o CX, o DX, o EX) sia detto dv (o dw, o dy, o dz) ossia differenza delle stesse v (o delle stesse w, o delle y, o delle z). […]” Il differenziale di 𝑣 è, dunque, il segmento quarto proporzionale 𝑑𝑣:𝑑𝑥=𝑣:𝐵𝑋. Si nota che nella definizione né 𝑑𝑥, né 𝑑𝑦 sono infinitesimi. Il differenziale è definito per mezzo della tangente e non viceversa. Gli infinitesimi entrano in gioco quando Leibniz definisce la tangente a una curva come la retta che congiunge due punti della curva a distanza infinitamente piccola. D’altra parte l’interpretazione dei differenziali come infinitesimi è obbligatoria se si vuol dare un senso ad altre affermazioni di Leibniz, ad esempio: - Nella stessa definizione di differenziale, 𝑑𝑦 è l’incremento della variabile 𝑦. Tuttavia 𝑑𝑦 è la differenza delle ordinate sulla retta tangente e non sulla curva, due concetti diversi se 𝑑𝑥 è finito, che si possono confondere se 𝑑𝑥 è infinitesimo. - Le regole di differenziazione del prodotto e del quoziente si comprendono solo supponendo 𝑑𝑥 e 𝑑𝑦 infinitesimi e trascurando gli infinitesimi di ordine superiore. In questo lavoro, Leibniz indica anche le regole per il differenziale della somma, del prodotto e del quoziente di due funzioni e la regola per trovare 𝑑(𝑥𝑛). Le regole esposte sono che se 𝑎 è una quantità costante 𝑑𝑎=0 e 𝑑𝑎𝑥=𝑎𝑑𝑥;𝑑(𝑧−𝑦+𝑤+𝑥)=𝑑𝑧−𝑑𝑦+𝑑𝑤+𝑑𝑥;𝑑𝑥𝑦=𝑦𝑑𝑥+𝑥𝑑𝑦, e infine, posto 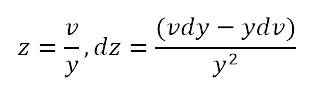 In questo modo si possono trovare le derivate di una potenza e poi da queste le derivate di una radice osservando che se 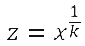 , si ha
x = zk
e derivando si ottiene dx = k zk-1 dz,
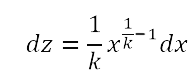da cui, infine,  .Il nuovo metodo viene utilizzato da Leibniz nella memoria del 1684 per risolvere alcuni problemi: un problema di minimo (la determinazione del cammino di un raggio rifratto, ovvero la legge della rifrazione), la determinazione della tangente a una curva data, la determinazione della curva avente sottotangente costante. |
| 1.2 Newton e il calcolo infinitesimale (a cura di Giulia Bartolotti) |
| Newton afferma di essere stato condotto alle sue
scoperte nel campo dell’analisi dalla lettura dell’opera Arithmetica
infinitorum di John Wallis, del 1656. Proprio da quest’opera,
trae ispirazione per trovare lo sviluppo in serie del binomio, che a
suo dire rappresenta il primo passo verso la creazione del suo “metodo
delle flussioni”. Newton, compie le più grandi scoperte nel campo della matematica nel 1665, quando è costretto a tornare a casa a causa della peste. Newton pubblica i suoi lavori fondamentali sul calcolo infinitesimale solo molto tempo dopo averli scritti. La prima esposizione stampata della sua teoria delle flussioni compare nell’Algebra di Wallis,1685, di cui Newton scrive alcune pagine. Un’altra grande opera di Newton, che verrà stampata nel 1736 post morte da John Colson, è De Methodis Serierum et Fluxionum (Method of Fluxions). Newton presenta il calcolo infinitesimale con due approcci e due notazioni differenti, l’uno in termini di “momenti”, l’altro in termini di “fluenti” e “flussioni”. Metodo dei momenti 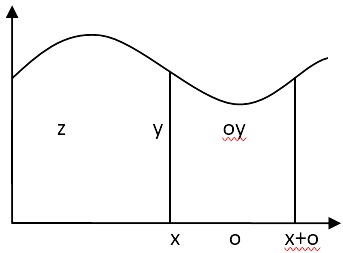 Con questo procedimento Newton non indica solamente un metodo generale per trovare il tasso di variazione istantaneo di una variabile rispetto ad un'altra, ma dimostra anche che l'area puಠessere ottenuta invertendo il procedimento di ricerca del tasso di variazione. Questa scoperta, cioè che le somme o pi๠precisamente i limiti di somme, possono essere ricavati invertendo la differenziazione, è quello che viene oggi chiamato teorema fondamentale del calcolo integrale. Dopo aver dimostrato che la derivata dell'area sottesa dalla curva, con grafico y(x), è uguale al valore della y e aver asserito che anche il viceversa è vero, Newton trova la regola secondo cui, se il valore della y è una somma di termini, allora l'area è la somma delle aree che risultano da ciascuno dei termini. In linguaggio moderno, l'integrale definito di una somma di funzioni è uguale alla somma degli integrali definiti delle singole funzioni. Metodo delle flussioni Considera le sue variabili come generate dal moto continuo di punti, rette e piani, piuttosto che come aggregati di elementi infinitesimi. Chiama ora fluente una quantità variabile e flussione il suo tasso di variazione e adopera la notazione 
e  per le flussioni delle fluenti x e y. La
flussione di è  , ecc., mentre la fluente di cui
x è la flussione viene denotata con x' e la fluente di quest'ultima con
x''. Newton pensa alle grandezze variabili con il tempo e se o è un intervallo infinitamente piccolo di tempo, allora 
e  sono gli incrementi infinitesimi di x e di y,
o i momenti di x e di y. Per trovare la relazione fra
e ; supponiamo, ad esempio, che la fluente sia y
= xn. Newton scrive anzitutto 
, e procede poi sviluppando il secondo membro con il teorema del
binomio, sottrae y = xn,
divide tutto per o, trascura tutti i termini che contengono ancora o e
ottiene 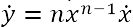 . In notazione moderna il risultato precedente si scrive 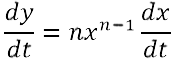 poiché dy/dx = ((dy/dt))/((dx/dt)), trovando il rapporto fra dy/dt e dx/dt, cioè fra e , si ottiene anche dy/dx.
|