II. 3. Archimede di Siracusa

 

Scarsi sono i particolari sulla vita di Archimede, ma possiamo ricavare qualche informazione su di lui dalle storie di Plutarco, Livio e altri autori. Plutarco, descrivendo l'assedio di Siracusa da parte dei romani durante le Seconda Guerra Punica, ci dice che Archimede abbia inventato ingegnose macchine da guerra per tenere lontano il nemico: catapulte [29] per lanciare pietre, corde, carrucole e ganci per sollevare e schiantare le navi romane, dispositivi per sviluppare incendi sulle navi (come questi dispositivi potessero essere realizzati e se realmente Archimede sia stato in grado di realizzarli, ci è spiegato da Archimede e gli specchi ustori [30]). Durante il saccheggio della città, Archimede venne trucidato da un soldato romano, nonostante che il generale Marcello avesse dato l'ordine di salvare la vita del matematico. Poiché, a quanto viene riferito, Archimede aveva settantacinque anni, è molto probabile che fosse nato nel 287 a.C.
Alcuni autori riportano che abbia visitato l'Egitto e che abbia studiato ad Alessandria con gli allievi di Euclide: fu probabilmente in questa occasione che inventò il dispositivo, oggi noto come "vite di Archimede" [31], fatto di canali o tubi avvolti elicoidalmente attorno ad un asse inclinato, munito di una manovella per farlo girare.
I vari resoconti rimastici sulla vita di Archimede sono d'accordo nel dipingerlo come persona che attribuiva scarso valore ai suoi congegni meccanici rispetto ai prodotti della sua attività intellettuale. Anche quando trattava di leve e di altre macchine semplici, era molto più interessato ai principi generali che le governavano che alle loro applicazioni pratiche.
Le opere di Archimede sopravvissute sono le seguenti:

Di questo trattato, in due libri, fanno parte gli studi di Archimede sul principio della leva [32]. Il primo libro prende in considerazione figure rettilinee e si chiude con la discussione sui centri di gravità del triangolo e del trapezio. Il secondo libro concentra l'attenzione sul centro di gravità di un segmento di parabola e comprende una dimostrazione del fatto che questo centro si trova sul diametro del segmento e divide questo diametro in segmenti che stanno nel rapporto di 3 a 2. Il procedimento usato per la dimostrazione è il metodo di esaustione.

Quest'opera, in due libri, contiene dei risultati molto importanti. Fra le proposizioni iniziali ve ne sono due che formulano il noto principio della spinta idrostatica di Archimede [33].

Qualsiasi solido più leggero di un fluido, se collocato nel fluido, si immergerà in misura tale che il peso del solido sarà uguale al peso del fluido spostato (Lib. I, Prop. 5).

Un solido più pesante di un fluido, se collocato in esso, discenderà in fondo al fluido e se si peserà il solido nel fluido, risulterà più leggero del suo vero peso, e la differenza di peso sarà uguale al peso del fluido spostato (Lib. I, Prop. 7).

Oltre alle proprietà dei fluidi, questo trattato contiene molte altre scoperte. Quasi tutto il secondo libro, per esempio, tratta della posizione di equilibrio di segmenti di paraboloidi quando siano immersi in un fluido, mostrando che la posizione di quiete dipende dal peso specifico relativo del paraboloide solido e del fluido in cui galleggia.

Questo piccolo trattato, che è probabilmente incompleto nella forma in cui ci è pervenuto, comprende solo tre proposizioni ( è possibile vedere gli enunciati nel sito Sulla misura del cerchio [34]), una delle quali è la dimostrazione, mediante il metodo di esaustione, del teorema secondo cui l'area del cerchio è uguale a quella di un triangolo rettangolo che abbia come lati la circonferenza e il raggio del cerchio stesso.
Nel suo calcolo approssimato del rapporto tra circonferenza di un cerchio e diametro, Archimede diede una ulteriore prova della sua abilità nel calcolo. Partendo dall'esagono regolare inscritto, egli calcolò i perimetri dei poligoni ottenuti raddoppiando successivamente il numero dei lati fino a raggiungere novantasei lati. Il risultato dal calcolo archimedeo relativo alla circonferenza era costituito da un'approssimazione del valore di 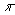espressa dalla disuguaglianza 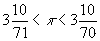, che era un valore migliore di quello ottenuto dagli egiziani e dai babilonesi. 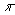(Va tenuto presente che né Archimede né alcun matematico greco fece mai uso della notazione per indicare il valore del rapporto tra circonferenza di un cerchio e il suo diametro.)

Questo trattato fu molto ammirato ma poco letto, poiché veniva considerato come la più difficile fra tutte le opere di Archimede.
La spirale viene definita come il luogo piano di un punto che, partendo dall'estremo di un raggio o semiretta, si sposta uniformemente lungo questo raggio mentre il raggio a sua volta ruota uniformemente intorno al suo estremo.
Lo studio che Archimede fece della spirale, curva che attribuiva all'amico Conone di Alessandria, si inquadrava nella scia delle ricerche, tipiche della matematica greca, volte a trovare le soluzioni dei tre famosi problemi classici. La curva si presta facilmente a effettuare molteplici sezioni dell'angolo. Come nel caso della quadratrice, però, essa può anche servire a quadrare il cerchio, come mostrò lo stesso Archimede.
Nel punto P si tracci la tangente alla spirale OPR, e questa tangente intersechi nel punto Q la retta che passa per O ed è perpendicolare a OP (vedi Fig. 1).

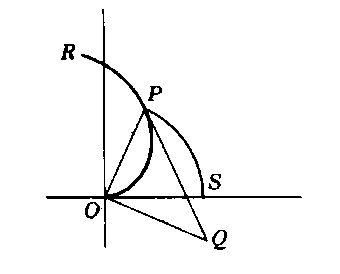Fig. 1

Archimede mostrava, mediante una dimostrazione per duplice reductio ad absurdum, che il segmento OQ (noto come la sottotangente polare relativa al punto P) era uguale in lunghezza all'arco di cerchio PS del cerchio avente come centro O e come raggio OP.
Se sulla spirale si sceglie un punto P come intersezione della spirale con la retta a 90° in coordinate polari, la sottotangente polare OQ sarà esattamente uguale a un quarto della circonferenza del cerchio di raggio OP. Pertanto l'intera circonferenza può essere costruita prendendo quattro volte il segmento OQ, e per mezzo del teorema di Archimede si trova un triangolo di area uguale all'area del cerchio. Una semplice trasformazione geometrica permetterà poi di sostituire il triangolo con un quadrato. E' così effettuata la quadratura del cerchio.
Gran parte dell'opera di Archimede è di natura tale che oggi verrebbe inclusa in un corso di analisi infinitesimale; ciò è particolarmente vero per il trattato Sulle spirali.
Si può analizzare la spirale di Archimede e le curve ad essa associate visitando il sito La spirale di Archimede [35]: attraverso Java (un linguaggio di programmazione progettato per eseguire operazioni evolute, indipendente dalla macchina su cui si opera) si possono manipolare i dati ed ottenere tutte le variazioni desiderate.

Al tempo in cui scriveva Archimede, le sezioni coniche erano note da quasi un secolo, e tuttavia non era stato fatto nessun progresso nel calcolo delle loro aree. Ci volle Archimede per quadrare una sezione conica, ossia un segmento della parabola e lo fece nella Proposizione 17 dell'opera in cui la quadratura costituiva l'obiettivo principale. La dimostrazione per mezzo del solito metodo di esaustione è lunga e complessa: comunque Archimede riuscì a dimostrare rigorosamente che l'area K di un segmento parabolico APBQC è uguale a quattro terzi dell'area di un triangolo avente la stessa base e uguale altezza (vedi Fig. 2).

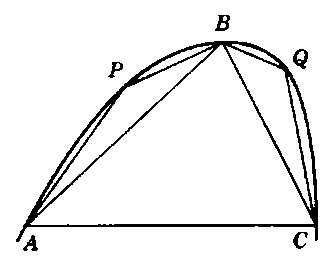Fig. 2

Nelle successive sette (e ultime) proposizioni, Archimede dava una seconda, ma diversa, dimostrazione del medesimo teorema. Egli dimostrava che l'area del triangolo inscritto maggiore, ABC, con base AC, è quattro volte la somma dei corrispondenti triangoli inscritti aventi come basi rispettivamente AB e BC. Continuando il processo suggerito da questa relazione, risulta chiaro che l'area H del segmento parabolico ABC è data dalla somma della serie infinita 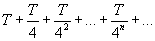, che è 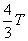. Archimede non parla di somma della serie infinita, perché ai suoi tempi i processi non finiti venivano disapprovati. Ricorrendo invece a una duplice reductio ad absurdum, Archimede dimostrava che H non poteva essere né maggiore né minore di . 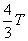(Archimede, come i suoi predecessori, non usava il termine "parabola", ma l'espressione "ortotomo", ossia "sezione di un cono retto".)
Nel preambolo alla Quadratura della parabola incontriamo l'assunzione che oggi è comunemente noto come l'assioma di Archimede:

L'eccesso per cui la maggiore di due aree disuguali supera la minore può, se sommato a se stesso, diventare superiore a qualsiasi area finita data.

Nel sito La teoria della misura da Archimede a Bonaventura Cavalieri [36] si può esaminare il procedimento di dimostrazione per la quadratura della parabola.

Nonostante Archimede non sia stato in grado di trovare l'area di un segmento qualsiasi di ellisse o di iperbole, in questo trattato riuscì a determinare l'area di tutta l'ellisse:

Le aree delle ellissi sono come i rettangoli formati dai loro assi (Prop. 6).

Ciò equivale a dire che l'area di un'ellisse è uguale all'area di un cerchio il cui raggio sia la media geometrica dei semiassi dell'ellisse. Inoltre, mostrava come trovare il volume di segmenti tagliati da un ellissoide, da un paraboloide o da un iperboloide (a due falde) di rivoluzione attorno all'asse principale. Il processo da lui usato è molto simile a quello impiegato dal metodo moderno di integrazione, differisce principalmente per la mancanza del concetto di limite di una funzione.

Archimede volle che sulla sua tomba fosse incisa la figura che rappresentava una sfera inscritta in un cilindro circolare retto la cui altezza è uguale al diametro della sfera ( per maggiori dettagli si veda La lapide di Archimede [37]): egli aveva, infatti, scoperto e dimostrato che il rapporto tra i volumi del cilindro e della sfera era uguale al rapporto tra le rispettive aree, cioè era un rapporto di tre a due. Inoltre sembra che Archimede sia stato il primo a scoprire e a dimostrare che l'area di una sfera è quattro volte l'area del suo cerchio massimo e che

la superficie di una qualsiasi calotta sferica è uguale al cerchio il cui raggio sia uguale al segmento tracciato dal vertice della calotta alla circonferenza del cerchio di base della calotta stessa.

Un teorema molto importante relativo alla superficie della sfera compare nella Proposizione 33, dopo una lunga serie di teoremi preliminari riguardanti la funzione seno:

Se in un segmento di cerchio L'AL' viene inscritto un poligono in modo che tutti i suoi lati, esclusa la base, siano uguali e il loro numero sia pari, come LK...A...K'L', ove A è il punto di mezzo del segmento; e se si tracciano le linee BB', CC', ... parallele alla base LL' e congiungenti coppie di punti angolari, allora (BB'+CC'+...+LM):AM=A'B:BA, ove M è il punto di mezzo di LL' e AA' è il diametro passante per M (vedi Fig. 3).

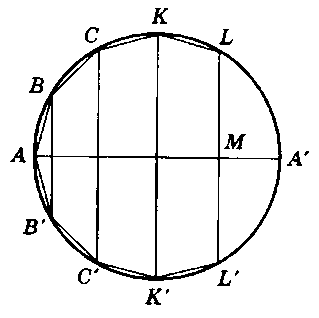Fig. 3

La nota formula per calcolare il volume della sfera compare nella Proposizione 34 del Libro I:

Qualsiasi sfera è uguale a quattro volte il cono che ha la base uguale al cerchio massimo della sfera e l'altezza uguale al raggio della sfera.

Il teorema viene dimostrato mediante il solito metodo di esaustione e come corollario ne segue il rapporto archimedeo fra i volumi e le aree della sfera e del cilindro circoscritto.

In quest'opera Archimede propone un sistema numerico capace di esprimere numeri superiori a 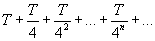nella notazione moderna. Egli sosteneva che questo numero era sufficientemente grande per contare i granelli di sabbia richiesti per riempire l'universo. Ciò era in risposta all'ipotesi avanzata da Aristarco di S'amo che la Terra si muovesse attorno al Sole.
E' possibile leggere l'intera opera tradotta in inglese visitando il sito l'Arenario [38].

La maggior parte dei trattati di Archimede rientrano nel campo della matematica superiore. Tuttavia il matematico non disdegnava di trattare problemi elementari. In quest'opera, per esempio, troviamo uno studio del cosiddetto arbelos (coltello del calzolaio). Questo è la regione delimitata da tre semicerchi che sono reciprocamente tangenti a due a due: l'area in questione è quella che si trova all'interno del semicerchio più grande e all'esterno dei semicerchi più piccoli. Vi è anche un teorema su quello che Archimede chiama salinon (saliera) e la nota trisezione archimedea dell'angolo.
Il libro dei lemmi non ci è pervenuto nel testo originale greco, ma attraverso una traduzione araba che più tardi venne tradotta in latino col titolo Liber assumptorum. Di fatto quest'opera, come ci è pervenuta, non può essere genuinamente archimedea, perché il nome di Archimede viene citato più volte nel corso del testo. Nondimeno, anche se questo trattato non è altro che una miscellanea di teoremi attribuiti ad Archimede dagli arabi, l'opera, nella sua sostanza, è probabilmente autentica.

Fra gli aspetti curiosi della tradizione attraverso la quale ci sono giunte le opere di Archimede vi è la scoperta, fatta nel nostro secolo, di uno dei suoi trattati più importanti, intitolato Il Metodo, di cui si erano perdute le tracce fin dai primi secoli dell'Era cristiana, finché non venne riscoperto nel 1906.
Qui, Archimede aveva reso pubblica una descrizione delle indagini "meccaniche" preliminari che lo avevano portato a fare la maggior parte delle sue principali scoperte matematiche.
Così come ci è pervenuto, contiene la maggior parte del testo di una quindicina di proposizioni inviate sotto forma di lettera a Eratostene, matematico e bibliotecario del Museo di Alessandria. L'autore iniziava dicendo che è più facile trovare la dimostrazione di un teorema se si ha già qualche conoscenza di ciò che esso comporta e che egli stesso possedeva un metodo o approccio meccanico che apriva la strada ad alcune delle sue dimostrazioni.

Ci sono dei riferimenti ad altre opere di Archimede andate perdute: Pappo riferisce di un lavoro sui poliedri semiregolari e di un trattato Sulle bilance e le leve; Teone menziona un trattato sugli specchi; lo stesso Archimede riferisce ne l'Arenario di un lavoro sul sistema numerico.
Diversamente dagli Elementi di Euclide, i trattati di Archimede sono pervenuti fino a noi tramite una tradizione manoscritta molto esile: quasi tutte le copie derivano da un unico originale greco che era ancora esistente all'inizio del XVI secolo e che era stato a sua volta copiato da un originale più antico risalente al IX o X secolo circa. Questa poca fortuna è dovuta probabilmente al fatto che le opere di Archimede non avevano un carattere didattico.

I risultati di Archimede, comunque, sono davvero notevoli. Egli è considerato da molti storici della matematica come uno dei più grandi matematici di tutti i tempi: era in grado di usare il metodo di esaustione, che era una prima forma di integrazione, per ottenere una grande quantità di risultati; aveva dato un'accurata approssimazione di 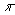; aveva inventato un sistema per esprimere grandi numeri; in meccanica è considerato il fondatore della statica e dell'idrostatica.