Richiami teorici
relativi a Trigonometria

Come è noto dalla geometria elementare :

Si chiama angolo ciascuna delle due parti del piano in cui esso è diviso da due semirette ( lati ) aventi origine comune O ( vertice ), incluse le due semirette. Quando i lati dell'angolo sono coincidenti l'angolo è nullo se formato dalla sola semiretta dei lati, è giro se è formato da tutti i punti del piano.

E' usuale indicare gli angoli e la loro misura con lettere greche minuscole a,b,c,...
Per misurare un angolo occorre fissarne l'unità di misura .

Misura in GRADI

• Gradi sessagesimali
  Si definisce grado sessagesimale la 360 ^a parte dell'angolo giro
• Gradi centesimali
  Si definisce grado centesimale la 400 ^a parte dell'angolo giro
  

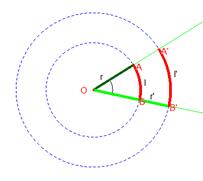
Conversione gradi sessagesimali - gradi centesimali

a°(cent) : a°(sess) = 360 : 400

Misura in RADIANTI

La definizione si basa sulla relazione esistente tra archi che sottendono uno stesso angolo al centro in circonferenze di raggio diverso :

l : r = l' : r' Il rapporto l/r si mantiene costante e viene quindi assunto come misura, in radianti, dell'angolo corrispondente arad = l / r Avrà misura arad = 1 radiante l'angolo al centro che sottende un arco di lunghezza uguale al raggio

Conversione gradi sessagesimali - radianti

Dalle definizioni precedenti segue la seguente relazione :

a° : a_rad = 360° : 2p

Più semplicemente basta ricordare che, per trasformare la misura di un angolo da gradi sessagesimali a radianti, occorre moltiplicare per p/180 e, viceversa, per trasformare la misura da radianti a gradi sessagesimali, occorre moltiplicare per 180/p.

a° = a_rad ( 180°/p )

a_rad = a° (p/180° )

Esempio : Qual'è la misura in gradi sessagesimali di un angolo che misura 1 radiante?

a°= 1(180°/p)≈ 180°/3,14 ≈ 57,32 °