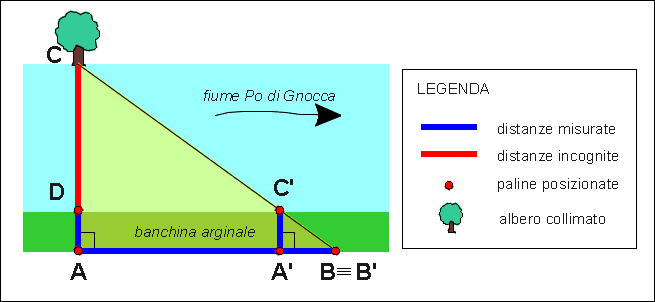
Calcolo della larghezza di un fiume con i triangoli SIMILI

Dall'esame di figura si deduce che i due triangoli ABC e A'B'C' sono simili in quanto hanno gli angoli corrispondenti congruenti (gli angoli in B e in B' sono congruenti perché coincidenti, l'angolo in A è congruente all'angolo in A' perché entrambi retti e di conseguenza l'angolo in C è congruente all'angolo in C'). I due triangoli,per il I° criterio di similitudine, avranno allora i lati corrispondenti in proporzione e cioè:
AB:A'B'=AC:A'C'
Poiché il rapporto fra segmenti è uguale al quoziente delle loro misure misure
AC=(AB/A'B')·A'C'
Essendo AD noto e CD=AC - AD
possiamo calcolare CD
Le distanze misurate con cordella metallica (clicca qui per vedere le foto di campagna), sono state le seguenti:
| AB=79,13m | A'B'= 3,98m | A'C'=AD=5,25m |
da cui deriva, applicando le relazioni viste sopra CD=99,13 m a cui, per precisione si deve togliere la porzione di golena di 9m, ottenendo alla fine una misura di 90,13 m.
Per verificare l'attendibilità del dato, si è eseguito in classe una verifica su una carta topografica alla scala 1:25.000.
Identificata la sezione di misura, è stata misurata una distanza pari a 0,36 cm; tale dato, moltiplicato per il fattore di scala equivale a 90m, in accordo con la distanza misurata in campagna.