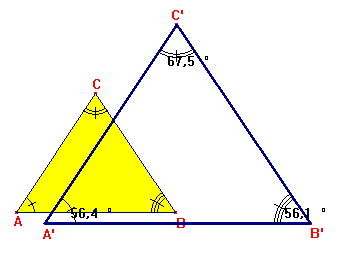
Similitudine tra triangoli
Definizione
Due triangoli si dicono simili se hanno ordinatamente gli angoli
uguali e i lati in proporzione.
Il
rapporto di due lati omologhi, ad esempio A'B' e AB, si chiama rapporto di similitudine.
Se il rapporto è uguale a 1 allora i triangoli sono congruenti: la congruenza tra triangoli è un caso particolare di
similitudine.
Per stabilire se due triangoli sono simili non è necessario verificare tutte le condizioni richieste nella definizione ,ma si puo’
ricorrere ad uno dei
criteri di similitudine:
I°
criterio di similitudine
Due
triangoli aventi gli angoli ordinatamente uguali, hanno i lati proporzionali.
Si può notare che questo risultato non vale per altri poligoni: basta pensare ad un quadrato ed ad un rettangolo con lati
diversi
II°
criterio di similitudine
Se
due triangoli hanno due lati in proporzione e l’angolo compreso uguale sono
simili.
III°
criterio di similitudine
Se
due triangoli hanno i lati ordinatamente
in proporzione sono simili.
Valgono
inoltre per i triangoli simili le
proprietà espresse dal