Le proporzioni tra grandezze

Esaminiamo il seguente esempio: 

il rapporto tra i segmenti A e B vale 5/3;   

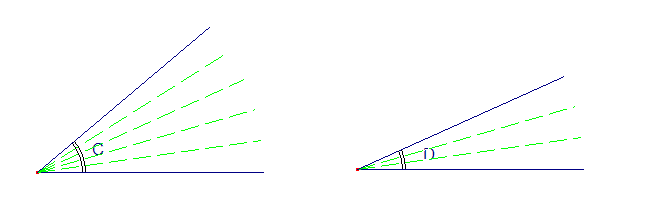
 il rapporto tra gli angoli C e D vale 5/3         

L’uguaglianza tra i rapporti si traduce in un nuovo concetto, quello di proporzione e si scrive

A:B=C:D

In generale

Quattro grandezze ordinate A,B,C,D, le prime due omogenee tra loro e le ultime due omogenee fra loro formano una 

proporzione se il rapporto fra A e B è uguale al rapporto fra C e D.

Le grandezze A,B,C,D sono i termini della proporzione:

A e C sono chiamati antecedenti; A e D sono gli estremi, B e C sono i medi; D viene chiamato quarto proporzionale.

Teorema   fondamentale sulle proporzioni fra grandezze.

Quattro grandezze, a due a due omogenee, formano una proporzione se e solo se sono in proporzione le rispettive misure.

Questo teorema permette di estendere alle proporzioni tra grandezze, le proprietà delle proporzioni numeriche.

Ricordiamo il

Teorema fondamentale sulle proporzioni numeriche  

Quattro numeri reali positivi ordinati sono in proporzione se e soltanto se il prodotto dei medi è uguale al prodotto tra gli estremi 

    Proprietà

     Supponiamo siano A,B,C, e D quattro grandezze in proporzione cioè         A:B=C:D

     Ne consegue che:

1. Se A > B allora  C > B e viceversa; se A < B allora C < D e viceversa;

2. B:A=D:C ( proprietà dell’invertire)

3. (A+B):B=(C+D):D ( proprietà del comporre)

4. Qualora gli antecedenti siano maggiori dei conseguenti  (A- B):B = (C-D):D  (proprietà dello scomporre)

5. Qualora tutte le grandezze siano fra loro omogenee            A:C = B:D        (proprietà del permutare i medi)

6. Qualora tutte le grandezze siano fra loro omogenee            D:B = C:A        (proprietà del permutare gli estremi)

Classi di grandezze direttamente proporzionali

Premesso che la teoria della proporzionalità tra classi di grandezze richiede il concetto di corrispondenza tra gli elementi delle classi considerate e che gli esempi e le applicazioni più significative ai fini didattici  richiedono il caso di corrispondenza biunivoca, ci limitiamo a considerare solo il caso di proporzionalità tra classi in corrispondenza biunivoca.

Consideriamo il seguente esempio:  

è data una classe  A di segmenti a,b,c…  costruiamo la classe A’ di rettangoli di stessa altezza h e di base  rispettivamente a,b,c…  

Tra le classi si stabilisce la corrispondenza che ad ogni segmento della classe A associa il rettangolo con base il segmento fissato e altezza h. Tale corrispondenza risulta biunivoca.  

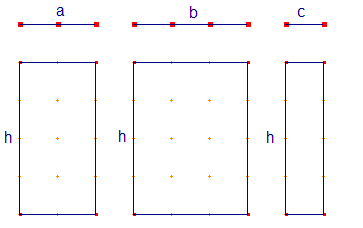
Dalla figura risulta che il rapporto tra a e b è uguale al rapporto tra i corrispondenti rettangoli; più in generale risulta che il rapporto tra segmenti della prima classe è uguale al rapporto tra i corrispondenti rettangoli.

Questo esempio suggerisce la seguente

Definizione. Le grandezze di due classi in corrispondenza biunivoca si dicono direttamente proporzionali quando il rapporto di due  grandezze qualunque della prima classe è uguale al rapporto delle due grandezze corrispondenti della seconda classe.

Vale inoltre il seguente

Criterio di Proporzionalità. Condizione necessaria e sufficiente affinchè due classi complete di grandezze in corrispondenza biunivoca siano direttamente proporzionali è che a grandezze uguali di una classe corrispondano grandezze uguali dell’altra e che alla somma di due grandezze qualunque di una classe corrisponda la somma delle grandezze corrispondenti dell’altra.

L’esempio considerato si traduce nel seguente risultato:

rettangoli di uguale base (uguale altezza) sono proporzionali alle rispettive altezze (alle rispettive basi)

o passando dalle grandezze alle misure:

le aree di rettangoli di uguale base(di uguale altezza) stanno tra loro come le lunghezze delle rispettive altezze (delle rispettive basi).

Ne viene che

Date due classi di grandezze in corrispondenza biunivoca, siano x e y  le misure di due elementi corrispondenti con y/x =costante= h cioè y= hx  allora le due classi sono direttamente proporzionali .

Infatti da y’=hx’ e y=hx discende:

a)    qualora x=x’ allora  risulta y=y’

b)    inoltre ad x+x’ rimane associato h(x+x’), e quindi per la proprietà distributiva della moltiplicazione rispetto all’addizione 

hx+hx’ ,cioè y+y’.

Per il criterio generale di proporzionalità le due classi sono direttamente proporzionali.

Viceversa vale il

Teorema della costante di proporzionalità.

Se due classi di grandezze sono direttamente proporzionali allora il quoziente tra le misure di due grandezze corrispondenti è una costante (indipendente dalla scelta della coppia di grandezze corrispondenti).

Dimostrazione

Siano x₀ e y₀  le misure di due prefissate grandezze corrispondenti e x e y le misure di due qualsiasi grandezze corrispondenti. 

Ne viene che

da x₀/x=y₀/y  discende  y/x =y₀/x_o.

Detto h il quoziente tra y₀ e x₀ ne  viene che il quoziente tra le misure di due grandezze corrispondenti è lo stesso per ogni coppia.

Tale costante prende il nome di costante di proporzionalità.