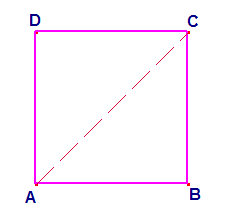
Vogliamo dimostrare che sono incommensurabili.
Ragioniamo per assurdo e supponiamo che che AC e AB siano segmenti commensurabili, ossia che ammettano una grandezza sottomultipla comune U,contenuta m volte in AC e n volte in AB. Ne consegue che n AC =m AB. Applicando il teorema di Pitagora al triangolo ABC , si perviene a n2= 2 m2. Si è giunti ad un assurdo perché n2 contiene 2 elevato ad esponente pari, mentre il secondo membro contiene 2 elevato ad esponente dispari. Tale assurdo consegue dall’aver supposto AC e AB commensurabili. Ne consegue che la diagonale e il lato del quadrato sono segmenti incommensurabili.
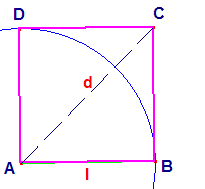
Riprendiamo
il caso precedente e confrontiamo diagonale e lato del quadrato:
si
scopre che l<d<2l, cioè riportando l su d si nota che
l è contenuto
una sola volta con il resto di r.
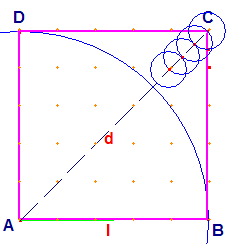
Riportando 1/10 di l su r si nota che è contenuto 4 volte con resto s, per cui
1,4 l<d<1,5 l
Ripetendo il procedimento non arriveremo mai ad un resto nullo: infatti se lo trovassimo, il rapporto sarebbe traducibile mediante un numero decimale finito e quindi la diagonale e il lato sarebbero grandezze commensurabili. Nè può verificarsi che da un certo punto in poi le cifre si possano ripetere, perché in tal caso il rapporto sarebbe un numero decimale periodico, quindi ancora razionale.
In
conclusione col procedimento indicato si viene a costruire un allineamento
decimale, illimitato, non periodico.
Poiché
l’unione dei numeri razionali positivi e dei numeri irrazionali positivi
costituisce l’insieme dei numeri reali positivi,possiamo affermare che
Il
rapporto di due grandezze omogenee è un numero reale (positivo);
esso è un numero razionale nel caso di grandezze commensurabili,
irrazionale nel caso di grandezze incommensurabili.