Classi di grandezze

Gli allievi hanno già acquisito dallo studio dei segmenti alcuni importanti concetti inerenti

- la possibilità di confrontare tra loro due segmenti qualsiasi e quindi stabilire se sono uguali o, se non lo sono, quale dei due è il maggiore

- la possibilità di introdurre una operazione di addizione, che gode delle proprietà associativa e commutativa.

Si possono in verità introdurre concetti analoghi anche per altri insiemi, quali gli angoli, gli archi di una stessa circonferenza, le superfici piane considerate come estensione.

Questi importanti esempi giustificano l’introduzione di un nuovo ente:

Si dice classe di grandezze ogni insieme tale che due suoi qualunque elementi possono essere “confrontati” e “sommati”. 

Due grandezze della stessa classe si dicono omogenee.

Si possono estendere i concetti di multiplo e di sottomultiplo già visti per i segmenti, a tutte le altre grandezze.

Per cui una grandezza A si dice multipla della grandezza B secondo il numero (naturale e non nullo) m se A coincide con B+B+….+B  (m addendi) e scriveremo A= m B  ovvero diremo che B è sottomultiplo di A e scriveremo B= (1/m) A.

Se la grandezza A è uguale alla somma di m grandezze eguali a (1/n) B scriveremo A = (m/n) B.

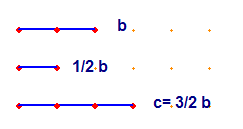
Ad esempio il segmento c, somma di 3 segmenti uguali ciascuno alla metà del segmento b, si indica con la scrittura c=(3/2) b

Le grandezze commensurabili ed il loro rapporto

Dall’esempio proposto

risulta che a è sottomultiplo comune  di b e di c: diremo in tal caso che b e c sono commensurabili.

Questa situazione suggerisce la

Definizione. Due grandezze omogenee si dicono commensurabili quando ammettono una grandezza sottomultipla comune, cioè esiste una terza grandezza omogenea con le prime due che è contenuta un numero intero di volte in ciascuna di esse.

Date due grandezze commensurabili A e B  con (1/m) A= (1/n)B scriviamo anche A=(m/n)B: il numero m/n viene chiamato rapporto fra A e B e si scrive anche A/B=m/n o A:B=m/n.

Ne viene che il rapporto fra grandezze commensurabili è un numero razionale. Pertanto il rapporto di due  grandezze commensurabili è un numero razionale.

Per esempio nel caso dei segmenti (1)

b=(2/5) c  ovvero b:c = 2/5