APPLICAZIONI DELLA SIMILITUDINE

I teoremi di Euclide

I teoremi di Euclide possono essere visti come applicazione della similitudine dei triangoli.

I° Teorema di Euclide. In un triangolo rettangolo un cateto è medio proporzionale fra l’ipotenusa e la sua proiezione su di essa

II°  Teorema di Euclide. In un triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale fra le proiezioni dei cateti sull’ipotenusa stessa 

Vale inoltre il teorema

Se si costruiscono sui cateti e sull’ipotenusa di un triangolo rettangolo triangoli simili allora il triangolo costruito sull’ipotenusa equivale alla somma dei triangoli costruiti sui cateti    

Rapporto di similitudine o scala.  

Nelle piante degli edifici e nelle carte topografiche o geografiche il rapporto di similitudine prende il nome di scala:in una carta topografica nella scala da 1 a 10000, se la distanza  fra due punti sulla carta vale 1 cm,la distanza tra i punti del terreno corrispondenti vale 10000 cm cioè 100m.

Possiamo ricordare agli studenti che la necessità di rappresentare il territorio era già sviluppata presso le grandi civiltà medio orientali :i primi abbozzi cartografici furono realizzati  con incisioni su tavolette d'argilla. Testimonianze degne di menzione sono una tavoletta, trovata in Mesopotamia, databile intorno al 2400-2200 a.C., raffigurante i fiumi Tigri e Eufrate e  la città di Nippur, l'antico centro culturale dei Sumeri, e il cosiddetto "mappamondo babilonese", proveniente da Uruk, che rappresenta la Terra come un cerchio circondato dall'acqua.

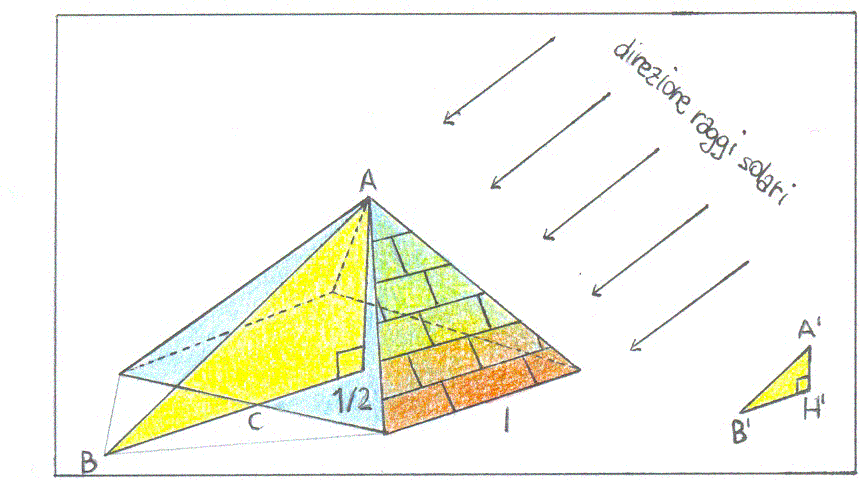
Come calcolare l'altezza di una piramide con un bastone

Dalla fig. 1 si può stabilire una proporzione tra i lati corrispondenti dei triangoli rettangoli simili ABH e A’B’H’, ossia

x:A’H’=HB:H’B’ dove x=AH (altezza della piramide), A’H’ è l’altezza del bastone, B’H’ ne è la sua ombra sul terreno e HB è

composto dal segmento BC (perpendicolare allo spigolo della piramide) e dalla metà  base della

piramide. Pertanto

  .

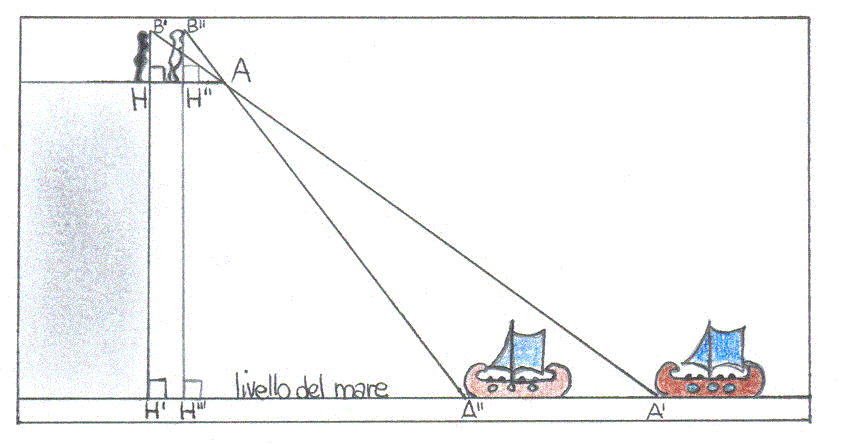
Come calcolare la distanza di una nave dalla costa

Sempre in ambito pratico inerente alla proporzionalità dei lati di triangoli simili, pare che Talete riuscisse a calcolare la

distanza di una nave dalla costa (fig. 2.1.2).Dalla fig.2 si ricava la distanza incognita x=H’A’ dalla proporzione dei lati

corrispondenti dei triangoli rettangoli simili ABH e A’BH’; si avrà H’B:HB=x:HA dove HB è l’altezza dell’occhio della

sentinella, H’B è composto da HH’ (altezza nota del dirupo dal livello del mare) e da HB, HA è

la distanza a cui si deve posizionare la sentinella per traguardare l’estremo della pedana con la punta della nave.

Si avrà

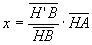
Analogamente si ragiona sui triangoli rettangoli simili AB’H’’ e A’’B’H’’’ con la nave nella nuova posizione A’’.

Sembra che i principi che stanno a fondamento del calcolo della distanza incognita di una nave fossero tuttavia già noti

in Egitto e in Mesopotamia, tuttavia pare che Talete avesse dato un sensibile contributo alla loro organizzazione

razionale