|
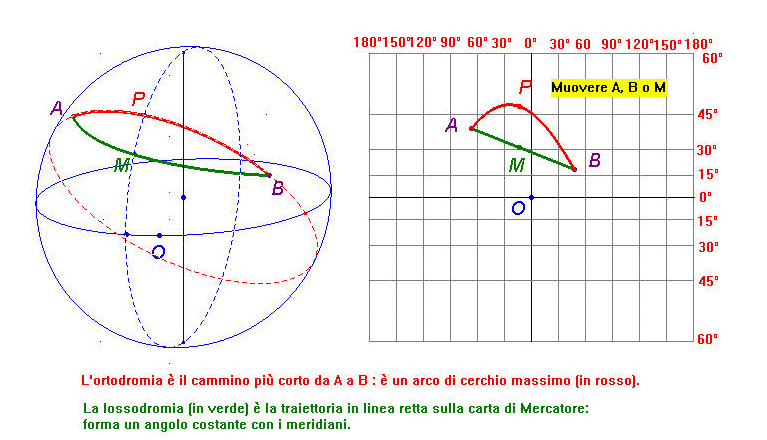
Dati due punti sulla superficie terrestre l'ortodromia (ortodromìa), dal greco ορθο-δρομέω "che corre dritto", è l’arco sulla superficie che
li congiunge formato dall’intersezione della superficie sferica con il piano di appartenenza dei due punti e del centro della Terra.
Il cerchio intersezione di tale piano con la superficie divide la
Terra in due emisferi e viene chiamato "cerchio massimo" (cerchi
massimi sono gli archi di geodetica della superficie sferica).
L’equatore è il solo cerchio massimo completo del reticolo geografico.
Ogni meridiano è la metà di un cerchio massimo. Nell'ipotesi di Terra
sferica tutti i meridiani hanno la stessa lunghezza e misurano metà dell’equatore. La lossodromia (lossodromìa o lossodròmia), dal greco λοζο-δρομέω
che significa "che corre obliquo", è una linea che taglia tutti i
meridiani con lo stesso angolo. Tutti i meridiani hanno una
lossodromia a 0° (nord) o 180° (sud), a seconda della direzione del
moto. L’Equatore e tutti gli altri paralleli hanno una lossodromia a
90° (est) o 270° (ovest). Tutte le altre lossodromie tagliano i
meridiani con un medesimo angolo che si ricava da una curva
conosciuta col nome di "curva lossodromica". Procedendo lungo questa
curva ci muoveremmo a spirale attorno alla Terra.
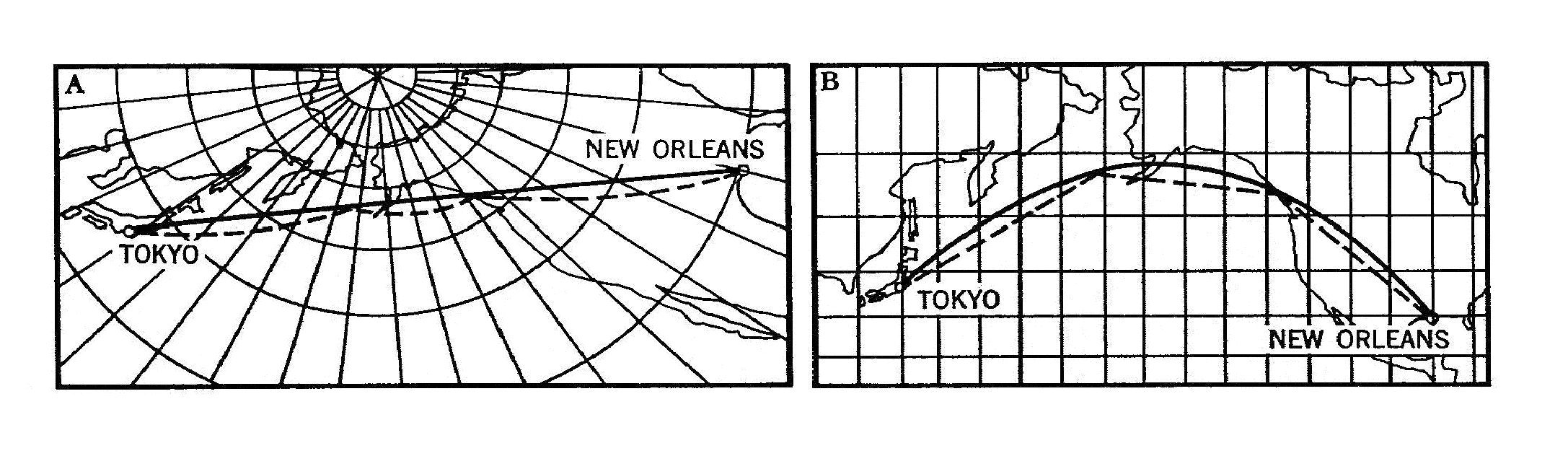
In aeronautica è conveniente percorrere traiettorie più brevi
possibili. Per questo si cerca di seguire, nello spostamento tra due
punti, la linea ortodromica che li congiunge. Tuttavia dover cambiare
direzione continuamente non è di grande praticità per i piloti. Per
facilitare le manovre nello spostamento tra due punti
si fa in modo che navi e aerei riescano ad accostarsi il più possibile
all’ortodromia e il moto viene diretto lungo
una serie di lossodromie che approssimano la linea ortodromica. I
cartografi, nel costruire mappe per la navigazione aerea o marittima,
usano spesso la proiezione cartografica di Mercatore, nel cui reticolo geografico i meridiani e i paralleli sono linee rette
perpendicolari e ogni linea retta tracciata sulla carta rappresenta
una lossodromia, naturalmente a discapito di altre proprietà. E’ bene
precisare che nel calcolo delle rotte non si tiene conto soltanto di
questi aspetti ma anche delle forze che intervengono nel moto di un
corpo rispetto ad un altro in rotazione uniforme, nel nostro caso la
Terra (forza centrifuga e forza di Coriolis). |

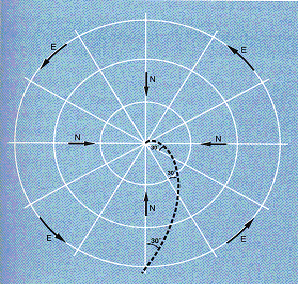
Curva lossodromica con angolo
costante di 30°
|